Inversion Algorithms Based on Deep Learning for Inverse Problems: Some Recent Progresses

doi:10.19596/j.cnki.1001-246x.8992

Abstract

Abstract:

Inverse problems are of wide and important applications in many areas such as radar and sonar, medical imaging, nondestructive testing and geophysical prospection. Inverse problems are ill-posed problems, so it is challenging to construct stable and highly effective inversion algorithms for them. One of the important methods to tackle this challenging issue is to devise an appropriate regularization strategy based on the a priori information of the unknown solution. The success of traditional regularization methods heavily depends on correctly encoding the a priori information of the unknown solution into the inversion algorithms, but this is in general very difficult in practical computation. With the development of deep learning techniques in recent years, it becomes possible to directly learn the a priori information of the unknown solutions of the inverse problems from data, which is helpful in developing highly effective and stable inversion algorithms. In this paper, we review some recent progres on inversion algorithms based on deep learning, focusing mainly on those based on learnable regularization framework. In addition, we also summarize the advantages and shortcomings of the inversion algorithms based on deep learning, and discuss their future research directions.

Key words: inverse problems, inverse scattering, deep learning, regularization method, learnable regularization framework

Kai LI, Bo ZHANG. Inversion Algorithms Based on Deep Learning for Inverse Problems: Some Recent Progresses[J]. Chinese Journal of Computational Physics, 2024, 41(6): 717-731.

Figures/Tables 5

Fig.1 Network architecture of NPDHG-CSNet

Fig.2 Reconstructed MRI images of NPDHG-CSNet under different sampling rates and the Cartesian sampling mask

Fig.3 Diagram of the projected iterative algorithm

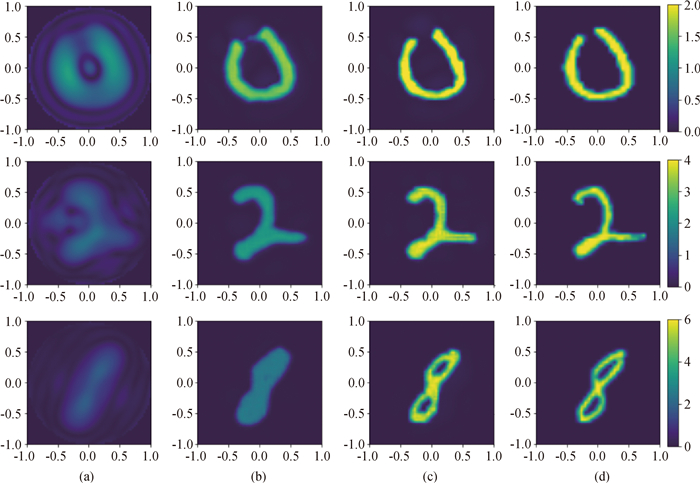
Fig.4 Reconstructed results by learned projected iterative algorithm (3rd column) (a)Landweber; (b) simplified learned projected scheme; (c) learned projected scheme; (d) ground truth

Fig.5 Generalization ability of learned projected iterative algorithm (a)Landweber; (b)learned projected algorithm; (c) ground truth

References 86

1	HADAMARD J . Lectures on Cauchy's problems in linear partial differential equations[M]. New Haven: Yale University Press, 1923.
2	TIKHONOV A N . On the stability of inverse problems[J]. Dokl. Akad.Nauk USSR, 1943, 39 (5): 195- 198.
3	TIKHONOV A N . Solution of ill-posed problems and the regularization method[J]. Dokl. Akad. Nauk USSR, 1963, 151 (3): 501- 504.
4	TIKHONOV A N . On the stability of the functional optimization problem[J]. USSR Computational Mathematics and Mathematical Physics, 1966, 6 (4): 28- 33. DOI
5	JOHN F . Numerical solution of the equation of heat conduction for preceding times[J]. Annali di Matematica Pura ed Applicata, 1955, 40 (1): 129- 142. DOI
6	JOHN F . Continuous dependence on data for solutions of partial differential equations with a prescribed bound[J]. Communications on Pure and Applied Mathematics, 1960, 13 (4): 551- 585. DOI
7	NATTERER F . The mathematics of computerized tomography[M]. Philadelphia: SIAM, 2001.
8	NATTERER F , WUBBELING F . Mathematical methods in image reconstruction[M]. Philadelphia: SIAM, 2001.
9	ENGL H W , HANKE M , NEUBAUIER A . Regularization of inverse problems[M]. Dordrecht: Springer, 1996.
10	KIRSCH A . An introduction to the mathematical theory of inverse problems[M]. Cham: Springer, 2011.
11	PLATO R , VAINIKKO G . On the regularization of projection methods for solving Ⅲ-posed problems[J]. Numerische Mathematik, 1990, 57, 63- 79. DOI
12	KALTENBACHER B , NEUBAUER A , SCHERZER O . Iterative regularization methods for nonlinear ill-posed problems[M]. Berlin: Walter De Gruyter, 2008.
13	SCHERZER O , GRASMAIR M , GROSSAUER H , et al. Variational methods in imaging[M]. New York: Springer, 2009.
14	BISSANTZ N , HOHAGE T , MUNK A , et al. Convergence rates of general regularization methods for statistical inverse problems and applications[J]. SIAM Journal on Numerical Analysis, 2007, 45 (6): 2610- 2636. DOI
15	STUART M A . Inverse problems: A Bayesian perspective[J]. Acta Numerica, 2010, 19, 451- 559. DOI
16	TIKHONOV A N , ARSENIN V . Solutions of ill-posed problems[M]. New York: Distributed Solely by Halsted Press, 1977.
17	PHILLIPS D L . A technique for the numerical solution of certain integral equations of the first kind[J]. Journal of the ACM, 1962, 9 (1): 84- 97. DOI
18	RUDIN L I , OSHER S , FATEMI E . Nonlinear total variation based noise removal algorithms[J]. Physica D, 1992, 60 (1/4): 259- 268.
19	BREDIES K , KUNISCH K , VALKONEN T . Properties of L1-TGV2:The one-dimensional case[J]. Journal of Mathematical Analysis and Applications, 2013, 398 (1): 438- 454. DOI
20	CHAMBOLLE A , LIONS P L . Image recovery via total variation minimization and related problems[J]. Numerische Mathematik, 1997, 76 (2): 167- 188. DOI
21	BREDIES K , KUNISCH K , POCK T . Total generalized variation[J]. SIAM Journal on Imaging Sciences, 2010, 3 (3): 492- 526. DOI
22	DAUBECHIES I , DEFRISE M , DE MOL C . An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57 (11): 1413- 1457. DOI
23	RUBINSTEIN R , BRUCKSTEIN A M , ELAD M . Dictionaries for sparse representation modeling[J]. Proceedings of the IEEE, 2010, 98 (6): 1045- 1057. DOI
24	BRUCKSTEIN A M , DONOHO D L , ELAD M . From sparse solutions of systems of equations to sparse modeling of signals and images[J]. SIAM Review, 2009, 51 (1): 34- 81. DOI
25	ARRIDGE S . Solving inverse problems using data-driven models[J]. Acta Numerica, 2019, 28, 1- 174. DOI
26	BENNING M , BURGER M . Modern regularization methods for inverse problems[J]. Acta Numerica, 2018, 27, 1- 111. DOI
27	LECUN Y , BENGIO Y , HINTON G . Deep learning[J]. Nature, 2015, 521 (7553): 436- 444. DOI
28	RAWAT W , WANG Zenghui . Deep convolutional neural networks for image classification: A comprehensive review[J]. Neural Computation, 2017, 29 (9): 2352- 2449. DOI
29	ZHAO Zhongqiu , ZHENG Peng , XU Shoutao , et al. Object detection with deep learning: A review[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30 (11): 3212- 3232. DOI
30	MINAEE S , BOYKOV Y , PORIKLI F , et al. Image segmentation using deep learning: A survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44 (7): 3523- 3542.
31	TIAN Chunwei , FEI Lunke , ZHENG Wenxian , et al. Deep learning on image denoising: An overview[J]. Neural Networks, 2020, 131, 251- 275. DOI
32	ZHANG Kai , ZUO Wangmeng , CHEN Yunjin , et al. Beyond a gaussian denoiser: Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 2017, 26 (7): 3142- 3155. DOI
33	KOETZIER L R , MASTRODICASA D , SZCZYKUTOWICZ T P , et al. Deep learning image reconstruction for CT: Technical principles and clinical prospects[J]. Radiology, 2023, 306 (3): e221257. DOI
34	ADLER J , ÖKTEM O . Solving ill-posed inverse problems using iterative deep neural networks[J]. Inverse Problems, 2017, 33 (12): 124007. DOI
35	GUPTA H , JIN K H , NGUYEN H Q , et al. CNN-Based projected gradient descent for consistent CT image reconstruction[J]. IEEE Transactions on Medical Imaging, 2018, 37 (6): 1440- 1453. DOI
36	LI Housen , SCHWAB J , ANTHOLZER S , et al. NETT: Solving inverse problems with deep neural networks[J]. Inverse Problems, 2020, 36 (6): 065005. DOI
37	ELIASOF M , HABER E , TREISTER E D . Deep regularizers for inverse problems[J]. Inverse Problems, 2024, 40 (1): 015006. DOI
38	LUNZ S, ÖKTEM O, SCHÖNLIEB C B. Adversarial regularizers in inverse problems[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal, Canada: Curran Associates Inc., 2018: 8516-8525.
39	YANG Yan, SUN Jian, LI Huibin, et al. Deep ADMM-Net for compressive sensing MRI[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain: Curran Associates Inc., 2016: 10-18.
40	YANG Yan , SUN Jian , LI Huibin , et al. ADMM-CSNet: A deep learning approach for image compressive sensing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42 (3): 521- 538. DOI
41	LUNDERVOLD A S , LUNDERVOLD A . An overview of deep learning in medical imaging focusing on MRI[J]. Zeitschrift Fur Medizinische Physik, 2019, 29 (2): 102- 127. DOI
42	CHEN Yutong , SCHÖNLIEB C B , LIÒ P , et al. AI-Based reconstruction for fast MRI—A systematic review and Meta-Analysis[J]. Proceedings of the IEEE, 2022, 110 (2): 224- 245. DOI
43	GVNGÖR A , DAR S U , ÖZTVRK S , et al. Adaptive diffusion priors for accelerated MRI reconstruction[J]. Medical Image Analysis, 2023, 88, 102872. DOI
44	CUI Zhuoxu , ZHU Qingyong , Cheng Jing , et al. Deep unfolding as iterative regularization for imaging inverse problems[J]. Inverse Problems, 2024, 40 (2): 025011. DOI
45	LI K , ZHANG B , ZHANG H . Reconstruction of inhomogeneous media by an iteration algorithm with a learned projector[J]. Inverse Problems, 2024, 40 (7): 075008. DOI
46	CHEN X , WEI Z , LI M , et al. A review of deep learning approaches for inverse scattering problems[J]. Progress in Electromagnetics Research, 2020, 167, 67- 81. DOI
47	ZHOU Yulong , ZHONG Yu , WEI Zhun , et al. An improved deep learning scheme for solving 2-D and 3-D inverse scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2021, 69 (5): 2853- 2863. DOI
48	GUO Rui , LIN Zhichao , SHAN Tao , et al. Physics embedded deep neural network for solving full-wave inverse scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2022, 70 (8): 6148- 6159. DOI
49	LIU Yu , ZHAO Hao , SONG Rencheng , et al. SOM-Net: Unrolling the subspace-based optimization for solving full-wave inverse scattering problems[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60, 1- 15.
50	YANG Fangshu , PHAM T A , GUPTA H , et al. Deep-learning projector for optical diffraction tomography[J]. Optics Express, 2020, 28 (3): 3905- 3921. DOI
51	NING Jianfeng , HAN Fuqun , ZOU Jun . A direct sampling-based deep learning approach for inverse medium scattering problems[J]. Inverse Problems, 2024, 40 (1): 015005. DOI
52	LIN Youzuo , THEILER J , WOHLBERG B . Physics-guided data-driven seismic inversion: Recent progress and future opportunities in full-waveform inversion[J]. IEEE Signal Processing Magazine, 2023, 40 (1): 115- 133. DOI
53	JIN Peng, ZHANG Xitong, CHEN Yinpeng, et al. Unsupervised learning of full-waveform inversion: Connecting CNN and partial differential equation in a loop[DB/OL]. arXiv, 2022: 07584(2022-03-18). https://arxiv.org/abs/2110.07584.
54	LI Shucai , LIU Bin , REN Yuxiao , et al. Deep-learning inversion of seismic data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58 (3): 2135- 2149. DOI
55	WU Yue , LIN Youzuo . InversionNet: An efficient and accurate data-driven full waveform inversion[J]. IEEE Transactions on Computational Imaging, 2020, 6, 419- 433. DOI
56	LUNZ S. Learned regularizers for inverse problems[M]//CHEN Ke, SCHINLIEB C B, TAI Xuecheng, et al. Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging, Cham: Springer, 2022: 1-21.
57	HALTMEIER M, NGUYEN L. Regularization of inverse problems by neural networks[M]. CHEN Ke, SCHINLIEB C B, TAI Xuecheng, et al. Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging, Cham: Springer, 2022: 1-29.
58	MCCANN M T , JIN K H , UNSER M . Convolutional neural networks for inverse problems in imaging: A review[J]. IEEE Signal Processing Magazine, 2017, 34 (6): 85- 95. DOI
59	MONGA V , LI Yuelong , ELDAR Y C . Algorithm unrolling: Interpretable, efficient deep learning for signal and image processing[J]. IEEE Signal Processing Magazine, 2021, 38 (2): 18- 44. DOI
60	WANG Na , SUN Jian . Model meets deep learning in image inverse problems[J]. CSIAM Transactions on Applied Mathematics, 2020, 1 (3): 365- 386. DOI
61	XU R, ZHANG B. NPDHG-CSNets: A deep learning approach for compressive sensing MRI: 报告编号缺失[R]: Preprint, 2024.
62	许锐航. 基于可学习正则化框架的磁共振图像重构算法研究[D]. 北京: 中国科学院大学, 2023.
63	DONOHO D L . Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52 (4): 1289- 1306. DOI
64	VALKONEN T . A primal-dual hybrid gradient method for nonlinear operators with applications to MRI[J]. Inverse Problems, 2014, 30 (5): 055012. DOI
65	SUN Pengpeng , YANG Fangshu , LIANG Hongxian , et al. Full-waveform inversion using a learned regularization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61, 1- 15.
66	COLTON D L , KRESS R . Inverse acoustic and electromagnetic scattering theory[M]. 4rd ed. Cham: Springer, 2019.
67	BAKUSHINSKII A B . The problem of the iterative-regularized Gauss-Newton method[J]. Zhurnal Vychislitel'noi Matematiki Matematicheskoi Fiziki, 1992, 32 (9): 1503- 1509.
68	HYUN C M , KIM H P , LEE S M , et al. Deep learning for undersampled MRI reconstruction[J]. Physics in Medicine and Biology, 2018, 63 (13): 135007. DOI
69	WEI Zhun , LIU Dong , CHEN Xudong . Dominant-current deep learning scheme for electrical impedance tomography[J]. IEEE Transactions on Bio-medical Engineering, 2019, 66 (9): 2546- 2555. DOI
70	LIU Zicheng , ROY M , PRASAD D K , et al. Physics-guided loss functions improve deep learning performance in inverse scattering[J]. IEEE Transactions on Computational Imaging, 2022, 8, 236- 245.
71	ADLER J , ÖKTEM O . Learned primal-dual reconstruction[J]. IEEE Transactions on Medical Imaging, 2018, 37 (6): 1322- 1332.
72	ULYANOV D , VEDALDI A , LEMPITSKY V . Deep image prior[J]. International Journal of Computer Vision, 2020, 128, 1867- 1888.
73	SHU Ziyu , ENTEZARI A . Sparse-view and limited-angle CT reconstruction with untrained networks and deep image prior[J]. Computer Methods and Programs in Biomedicine, 2022, 226, 107167.
74	SUN Yubao , YANG Ying , LIU Qingshan , et al. Learning non-locally regularized compressed sensing network with half-quadratic splitting[J]. IEEE Transactions on Multimedia, 2020, 22 (12): 3236- 3248.
75	JIN Bangti , LI Xiyao , QUAN Qiming , et al. Conductivity imaging from internal measurements with mixed least-squares deep neural networks[J]. SIAM Journal on Imaging Sciences, 2024, 17 (1): 147- 187.
76	HABER E , TENORIO L . Learning regularization functionals-a supervised training approach[J]. Inverse Problems, 2003, 19 (3): 611.
77	AFKHAM B M , CHUNG J , CHUNG M . Learning regularization parameter-maps for variational image reconstruction using deep neural networks and algorithm unrolling[J]. Siam Journal on Imaging Sciences, 2021, 37 (10): 105017.
78	KOFLER A , ALTEKR U GER F , ANTAROU Ba F , et al. Learning regularization parameter-maps for variational image reconstruction using deep neural networks and algorithm unrolling[J]. SIAM Journal on Imaging Sciences, 2023, 16 (4): 2202- 2246.
79	JIA Junxiong , WU Yanni , LI Peijun , et al. Variational inverting network for statistical inverse problems of partial differential equations[J]. Journal of Machine Learning Research, 2023, 24 (1): 9597- 9656.
80	GAO Yu , LIU Hongyu , WANG Xianchao , et al. A bayesian scheme for reconstructing obstacles in acoustic waveguides[J]. Journal of Scientific Computing, 2023, 97 (3): 53.
81	KAWAGUCHI K , BENGIO Y , KAELBLING L . Generalization in deep learning[M]. Cambridge: Cambridge University Press, 2022: 112- 148.
82	NEYSHABUR B, LI Z, BHOJANAPALLI S, et al. Towards understanding the role of over-parametrization in generalization of neural networks[DB/OL]. arXiv, 2018(2018-05-30). https://arxiv.org/pdf/1805.12076.
83	MOHRI M , ROSTAMIZADEH A , TALWALKAR A . Foundations of machine learning[M]. Cambridge: MIT Press, 2018.
84	CHEN D, TACHELLA J, DAVIES M E. Robust equivariant imaging: A fully unsupervised framework for learning to image from noisy and partial measurements[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). New Orleans, LA, USA: IEEE, 2022: 5637-5646.
85	ZHOU Kaiyang , LIU Ziwei , QIAO Yu , et al. Domain generalization: A survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45 (4): 4396- 4415.
86	FARAHANI A, VOGHOEI S, RASHEED K, et al. A brief review of domain adaptation[C]//Advances in Data Science and Information Engineering: Proceedings From ICDATA 2020 and IKE. Las Vegas, USA: ICDATA, 2021: 877-894.

[1]	Dong LIU, Qilong CHEN, Xueqiang WANG. Deep Learning Method for Solving Linear Integral Equations Through Primitive Function Transformation [J]. Chinese Journal of Computational Physics, 2024, 41(5): 651-662.
[2]	Guozheng WU, Fajie WANG, Suifu CHENG, Chengxin ZHANG. Numerical Simulation of Forward and Inverse Problems of Internal Sound Field Based on Physics-informed Neural Network [J]. Chinese Journal of Computational Physics, 2022, 39(6): 687-698.
[3]	Guangdong LIU, Kaiyin ZHANG. A Modified Contrast Source Inversion Method for Electrically Dispersive Media [J]. Chinese Journal of Computational Physics, 2022, 39(6): 699-706.
[4]	Yingdong LU, Duqu WEI. Power System Chaos Prediction Based on DLSTM with Genetic Attention Mechanism [J]. Chinese Journal of Computational Physics, 2022, 39(3): 371-378.
[5]	ZHANG Qingfu, YAO Jun, HUANG Zhaoqin, LI Yang, WANG Yueying. A Multiscale Deep Learning Model for Fractured Porous Media [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(6): 665-672.
[6]	ZHOU Huanlin, YAN Jun, YU Bo, CHEN Haolong. Identification of Thermal Conductivity for Transient Heat Conduction Problems by Improved Cuckoo Search Algorithm [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(2): 212-220.
[7]	LIU Guangdong, YU Guangqun, FAN Shimin. Three-Dimensional Time-Domain Electromagnetic Inverse Scattering Technique for Debye Dispersive Media [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2015, 32(4): 455-468.
[8]	WANG Qishen, LIU Minghui, ZHANG Lihua, HE Min. Reconstruction Flexural Stiffness of Symmetric Simple Supported Beams with Single Mode [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2014, 31(2): 216-222.
[9]	JIANG Liang, XU Chenglong. Calibration Parameters in Non.Guassian 0ne.factor Short-term Rate Model with Regularization Method [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2012, 29(6): 837-844.
[10]	YANG Xin, LI Rundong, LIU Hangang, WANG Guanbo, WANG Kan. An Unfolding Method of NDP Based on Probability Iteration [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2012, 29(6): 891-900.
[11]	PAN Wenfeng, ZONG Zhixiong, YOU Yunxiang, MIAO Guoping. Fast Acoustic Far-field Inverse of Three-dimensional Scattering Objects in an Ocean Waveguide [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2010, 27(1): 121-130.
[12]	XUE Qi-wen, YANG Hai-tian, HU Guo-jun. A Conjugate Gradient Method for Inverse Heat Conduction Problems with Multi-variables in Transient-state [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2005, 22(1): 56-60.
[13]	ZHUANG Hong-wei, MA Yi-chen, ZHANG Zhi-bin, WANG Jian. Reconstruction of the Shape of Unknown Obstacles in Freshwater [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2004, 21(1): 54-60.
[14]	YANG Feng, NIE Zai-ping. AN EFFICIENT INVERSION OF THE FORMATION CONDUCTIVITY DISTRIBUTION BASED ON THE INDUCTION MEASUREMENTS [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2000, 17(S1): 89-94.
[15]	XIAO TING-yan, SONG Jin-lai. A DISCRETE REGULARIZATION METHOD FOR THE NUMERICAL INVERSION OF ABEL TRANSFORM [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2000, 17(6): 602-610.