Chinese Journal of Computational Physics ›› 2021, Vol. 38 ›› Issue (6): 661-671.DOI: 10.19596/j.cnki.1001-246x.8332
• Research Reports • Previous Articles Next Articles
Han XIAO, Chunxi LI, Haozhe SU, Xuemin YE( )
)
Received:2021-01-18
Online:2021-11-25
Published:2022-04-27
Contact:
Xuemin YE
CLC Number:
Han XIAO, Chunxi LI, Haozhe SU, Xuemin YE. Numerical Simulation on Instability of Vertical Liquid Drainage[J]. Chinese Journal of Computational Physics, 2021, 38(6): 661-671.
Add to citation manager EndNote|Ris|BibTeX
URL: http://www.cjcp.org.cn/EN/10.19596/j.cnki.1001-246x.8332
| 有量纲参数 | 符号 | 取值或变化范围 |
| 动力学弯月面长度/mm | l* | 0.36 |
| 液膜特征厚度/μm | d* | 10 |
| 动力黏度/(Pa·s) | μ | 10-3 |
| 表面黏度/(Pa·s·m) | μs + κs | 10-4~4×10-2 |
| 剪切黏度/(Pa·s·m) | μs | 10-5~2.1×10-4 |
| 密度/(kg·m-3) | ρ | 103 |
| 特征速率/(m·s-1) | U* | 9.8×10-4 |
| 扩散系数/(m2·s-1) | Ds* | 10-10~5×10-8 |
Table 1 Values of dimensional parameters
| 有量纲参数 | 符号 | 取值或变化范围 |
| 动力学弯月面长度/mm | l* | 0.36 |
| 液膜特征厚度/μm | d* | 10 |
| 动力黏度/(Pa·s) | μ | 10-3 |
| 表面黏度/(Pa·s·m) | μs + κs | 10-4~4×10-2 |
| 剪切黏度/(Pa·s·m) | μs | 10-5~2.1×10-4 |
| 密度/(kg·m-3) | ρ | 103 |
| 特征速率/(m·s-1) | U* | 9.8×10-4 |
| 扩散系数/(m2·s-1) | Ds* | 10-10~5×10-8 |
| 无量纲参数 | 符号 | 取值或变化范围 |
| 小量 | ε | 0.028 |
| Marangoni数 | M | 7~350 |
| Peclet数 | Pe | 100~30 000 |
| 表面黏度 | S | 7~300 |
| 剪切黏度 | S′ | 0.1~10 |
Table 2 Values of dimensionless parameters
| 无量纲参数 | 符号 | 取值或变化范围 |
| 小量 | ε | 0.028 |
| Marangoni数 | M | 7~350 |
| Peclet数 | Pe | 100~30 000 |
| 表面黏度 | S | 7~300 |
| 剪切黏度 | S′ | 0.1~10 |
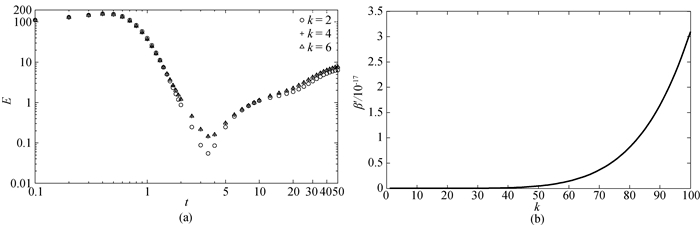
Fig.9 (a) The perturbation energy E as a function of time t, horizontal and vertical coordinates are in logarithmic forms; (b) The growth factor β′ as a function of disturbance number k
| 1 | HU Y, SUN T. Three-dimensional numerical simulation of dynamics characteristics of two rising bubbles with lattice Boltzmann method[J]. Chinese J Comput Phys, 2020, 37 (3): 277- 283. |
| 2 | SUN T, LIU Z B, FAN W, et al. Three-dimensional numerical simulation of vapor bubble rising in superheated liquid by lattice Boltzmann method[J]. Chinese J Comput Phys, 2019, 36 (6): 659- 664. |
| 3 | LOU Q, ZANG C Q, WANG H Y, et al. Interfacial dynamics of immiscible gas-liquid two-phase flow for CO2 in microchannel: Lattice Boltzmann method[J]. Chinese J Comput Phys, 2019, 36 (2): 153- 164. |
| 4 | YANG S D, YE X M, LI C X. Effect of surfactant concentration distribution on film drainage[J]. Chinese J Comput Phys, 2018, 35 (5): 577- 586. |
| 5 |
梁梅清, 殷鸿尧, 冯玉军. 智能水基泡沫研究进展[J]. 物理化学学报, 2016, 32 (11): 2652- 2662.
DOI |
| 6 |
杜东兴, 张娜, 孙芮, 等. 泡沫薄膜液在变径管内的流变学特性[J]. 化工学报, 2016, 67 (S1): 181- 185.
DOI |
| 7 | WANG F, LI Z M, LI S Y, et al. Mathematical model and numerical simulation of foam plug removal[J]. Chinese J Comput Phys, 2015, 32 (1): 58- 64. |
| 8 | MYSELS K J, SHINODA K, FRANKEL S. Soap films: Studies of their thinning and a bibliography[M]. Pergamon Press, 1959. |
| 9 |
SAULNIER L, CHAMPOUGNY L, BASTIEN G, et al. A study of generation and rupture of soap films[J]. Soft Matter, 2014, 10 (16): 2899- 2906.
DOI |
| 10 |
SAULNIER L, BOOS J, STUBENRAUCH C, et al. Comparison between generations of foams and single vertical films-single and mixed surfactant systems[J]. Soft Matter, 2014, 10 (29): 5280- 5288.
DOI |
| 11 |
BERG S, ADELIZZI E A, TROIAN S M. Experimental study of entrainment and drainage flows in microscale soap films[J]. Langmuir, 2005, 21 (9): 3867- 3876.
DOI |
| 12 |
BERG S, ADELIZZI E A, TROIAN S M. Images of the floating world: Drainage patterns in thinning soap films[J]. Phys Fluids, 2004, 16 (9): S6.
DOI |
| 13 |
SHABALINA E, BÉRUT A, CAVELIER M, et al. Rayleigh-Taylor-like instability in a foam film[J]. Phys Rev Fluids, 2019, 4 (12): 124001.
DOI |
| 14 |
SETT S, SINHA-RAY S, YARIN A L. Gravitational drainage of foam films[J]. Langmuir, 2013, 29 (16): 4934- 4947.
DOI |
| 15 |
SETT S, SAHU R P, SINHA-RAY S, et al. Superspreaders versus "cousin" non-superspreaders: Disjoining pressure in gravitational film drainage[J]. Langmuir, 2014, 30 (10): 2619- 2631.
DOI |
| 16 |
HUDALES J, STEIN H N. Profile of the plateau border in a vertical free liquid film[J]. J Colloid Interface Sci, 1990, 137 (2): 512- 526.
DOI |
| 17 |
STEIN H N. On marginal regeneration[J]. Adv Colloid Interface Sci, 1991, 34, 175- 190.
DOI |
| 18 |
NIERSTRASZ V A, FRENS G. Marangoni flow driven instabilities and marginal regeneration[J]. J Colloid Interface Sci, 2001, 234 (1): 162- 167.
DOI |
| 19 |
JOYE J, HIRASAKI G J, MILLER C A. Asymmetric drainage in foam films[J]. Langmuir, 1994, 10 (9): 3174- 3179.
DOI |
| 20 |
NAIRE S, BRAUN R J, SNOW S A. A 2+1 dimensional insoluble surfactant model for a vertical draining free film[J]. J Comput Appl Math, 2004, 166 (2): 385- 410.
DOI |
| 21 |
BRAUN R J, SNOW S A, PERNISZ U C. Gravitational drainage of a tangentially-immobile thick film[J]. J Colloid Interface Sci, 1999, 219 (2): 225- 240.
DOI |
| 22 |
WONG H, RUMSCHITZKI D, MALDARELLI C. On the surfactant mass balance at a deforming fluid interface[J]. Phys Fluids, 1996, 8 (11): 3203- 3204.
DOI |
| 23 |
HEIDARI A H, BRAUN R J, HIRSA A H, et al. Hydrodynamics of a bounded vertical film with nonlinear surface properties[J]. J Colloid Interface Sci, 2002, 253 (2): 295- 307.
DOI |
| 24 |
NAIRE S, BRAUN R J, SNOW S A. An insoluble surfactant model for a vertical draining free film with variable surface viscosity[J]. Phys Fluids, 2001, 13 (9): 2492- 2502.
DOI |
| 25 |
SADAKA G, RAKOTONDRANDISA A, TOURNIER P, et al. Parallel finite-element codes for the simulation of two-dimensional and three-dimensional solid-liquid phase-change systems with natural convection[J]. Comput Phys Commun, 2020, 257, 107492.
DOI |
| 26 |
VASU B, DUBEY A, BEG O A, et al. Micropolar pulsatile blood flow conveying nanoparticles in a stenotic tapered artery: Non-Newtonian pharmacodynamic simulation[J]. Comput Biol Med, 2020, 126, 104025.
DOI |
| 27 |
RODRIGUEZ J M, TABOADA-VAZQUEZ R. Numerical behaviour of a new LES model with nonlinear viscosity[J]. J Comput Appl Math, 2020, 377, 112868.
DOI |
| 28 | SNOW S, STEVENS R. Silicone surfactants[M]. CRC Press, 1999. |
| 29 |
PARK C. Effects of insoluble surfactants on dip coating[J]. J Colloid Interface Sci, 1991, 146 (2): 382- 394.
DOI |
| 30 |
GUPTA S, TIWARI N. Dip coating in the presence of an opposing Marangoni stress[J]. Eur Phys J E, 2017, 40 (1): 9.
DOI |
| 31 |
LI C X, LI M L, SHI Z X, et al. Effect of soluble surfactants on vertical liquid film drainage[J]. Phys Fluids, 2019, 31 (3): 32105.
DOI |
| 32 |
LI H, LI Z, TAN X, et al. Three-dimensional backflow at liquid-gas interface induced by surfactant[J]. J Fluid Mech, 2020, 899, A8.
DOI |
| 33 |
VITASARI D, GRASSIA P, MARTIN P. Surfactant transport onto a foam film in the presence of surface viscous stress[J]. Appl Math Model, 2016, 40 (3): 1941- 1958.
DOI |
| 34 |
WARNER M, CRASTER R V, MATAR O K. Fingering phenomena associated with insoluble surfactant spreading on thin liquid films[J]. J Fluid Mech, 2004, 510, 169- 200.
DOI |
| [1] | XU Yue, CUI Guomin. Heat Exchanger Network Optimization Using Structural Perturbation Strategy [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(6): 734-744. |
| [2] | LIU Yongqiang, ZHA Xuejun, WANG Qingsong, YANG Zhen, XIA Qinghao, WU Bin. Influence of Local Heat Source on Thermal Transport in Magnetic Island [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(2): 203-210. |
| [3] | YE Xuemin, JIANG Kai, LI Chunxi. Marangoni Effect on Soluble Surfactant Droplet Spreading in Different Spreading Systems [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2013, 30(5): 683-691. |
| [4] | ZHENG Wenli, LI Shushen, WANG Xuefeng. Energy Levels of Hydrogenic Impurities in Quantum Ring with Parabolic Potential of Finite Depth [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2013, 30(3): 463-468. |
| [5] | MEI Liquan, FANG Ye, YUAN Changqi. Rayleigh Quotient Iteration Algorithm for Source Inversion in Neutron Transport Problem [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2012, 29(3): 369-374. |
| [6] | JIN Wenliang, CHEN Xiangdong. General Multiphase Matching for Grover Quantum Search Algorithm [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2012, 29(1): 152-158. |
| [7] | CEHN Rongqian, WU Yizhao, XIA Jian. Simulation of Trailing Edge Noise Based on Stochastic Noise Generation and Radiation Method [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2011, 28(5): 698-704. |
| [8] | WANG Shengxi, SONG Songhe, ZOU Zhengping. A 3D Constrained Unstructured Mesh Generation Method with VBATM and Steiner Points Perturbation [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2010, 27(5): 649-657. |
| [9] | DAI Zihuan, WU Jiming, LIN Zhong, FU Shangwu. Subzonal Pressure Methods in Lagrangian Algorithm of Two-dimensional Three-temperature Radiation Hydrodynamics [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2010, 27(3): 326-334. |
| [10] | DONG Hefei, ZHANG Deliang, YANG Guowei. Perturbation Finite Volume Method and Application in Two-phase Flows [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2009, 26(6): 857-864. |
| [11] | ZHANG Jinping, CHEN Taihong, DAI Wei, LAN Xiaogang, YU Fei. EPR Spectra of CdCl2:Ni2+ Crystals:High-order Perturbation and Complete Diagonalization [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2009, 26(4): 579-585. |
| [12] | REN Xincheng, GUO Lixin. Optical Wave Transmission Through Slightly Gaussian Rough Surface of Layered Medium [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2009, 26(3): 422-430. |
| [13] | CHEN Taihong. Complete Diagonalization for Optical Spectra and EPR Spectra of NiF2 Crystals [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2008, 25(2): 218-224. |
| [14] | MEI Shuli, ZHANG Senwen, LU Qishao. A Wavelet Precise Integration Method for Burgers Equations Based on Homotopy Technique [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2007, 24(1): 54-58. |
| [15] | ZHANG Gen-xuan, LIU Ming-hou, CHEN Yi-liang, WANG Lu. Two-dimensional Theoretical and Numerical Investigation of Gaseous Slip Flows in a Micro-channel [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2006, 23(6): 685-691. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © Chinese Journal of Computational Physics
E-mail: jswl@iapcm.ac.cn
Supported by Beijing Magtech Co., Ltd.
