Improved Fifth-order WENO-Z+ Schemes Based on Modified Stencil

doi:10.19596/j.cnki.1001-246x.8654

Abstract

Abstract:

First, a modified stencil approximation method is introduced, which improves the second-order polynomial approximation of the numerical flux on each candidate sub-stencil in the classical fifth-order WENO-JS scheme. The stencil approximation reaches the fourth-order accuracy by adding a cubic correction term, and it has ENO property by introducing an adjustable function.Then the modified stencil approximation method is applied to WENO-Z+and WENO-Z+M schemes, and the modified WENO-Z+schemes based on the modified stencil type (WENO-MS-Z+, WENO-MS-Z+M) are developed.A series of numerical examples are used to test the new schemes. The results show that the new schemes have a strong ability to capture shock waves and high resolution for small-scale wave structures, which is significantly improved compared with the original WENO-Z+and WENO-Z+M schemes.

Key words: hyperbolic conservation laws, WENO-Z+, modified stencil, nonlinear weights

CLC Number:

O469

Cheng GUO, Pengdan CHENG, Yahui WANG. Improved Fifth-order WENO-Z+ Schemes Based on Modified Stencil[J]. Chinese Journal of Computational Physics, 2023, 40(6): 666-676.

Figures/Tables 9

Fig.1 Stencils for the fifth-order WENO numerical flux

Table 1 L1 errors and convergence rates at t=2 of different schemes for the linear advection Eq.(20) with the initial data ① of Eq.(21)

N	WENO-Z+		WENO-Z+M		WENO-MS-Z+		WENO-MS-Z+M
N	L¹ error	order	L¹ error	order	L¹ error	order	L¹ error	order
20	2.57 × 10^-4		3.40 × 10^-4		3.32 × 10^-4		3.13 × 10^-4
40	8.04 × 10^-6	5.00	9.60 × 10^-6	5.15	9.20 × 10^-6	5.17	9.01 × 10^-6	5.12
80	2.44 × 10^-7	5.04	2.56 × 10^-7	5.23	2.50 × 10^-7	5.20	2.44 × 10^-7	5.21
160	8.07 × 10^-9	4.92	7.61 × 10^-9	5.07	7.21 × 10^-9	5.11	6.97 × 10^-9	5.13
320	2.47 × 10^-10	5.03	2.38 × 10^-10	5.00	2.16 × 10^-10	5.06	2.06 × 10^-10	5.08

Table 2 L1 errors and convergence rates at t=2 of different schemes for the linear advection Eq.(20) with the initial data ② of Eq.(21)

N	WENO-Z+		WENO-Z+M		WENO-MS-Z+		WENO-MS-Z+M
N	L¹ error	order	L¹ error	order	L¹ error	order	L¹ error	order
20	4.36 × 10^-3		4.19 × 10^-3		1.95 × 10^-3		1.75 × 10^-3
40	1.37 × 10^-4	4.98	1.31 × 10^-4	4.99	6.10 × 10^-5	4.99	5.47 × 10^-5	5.00
80	4.58 × 10^-6	5.00	3.58 × 10^-6	5.19	1.56 × 10^-6	5.29	1.50 × 10^-6	5.19
160	1.43 × 10^-7	5.00	1.16 × 10^-7	4.95	4.41 × 10^-8	5.14	4.23 × 10^-8	5.15
320	4.44 × 10^-9	5.03	3.57 × 10^-9	5.02	1.38 × 10^-9	5.00	1.32 × 10^-9	5.00

Fig.2 Density contours of Sod shock tube problem on 200 grid points at t=2, CFL=0.6

Fig.3 Density contours of Lax shock tube problem on 200 grid points at t=1.3, CFL=0.6

Fig.4 Density contours of Shock wave interaction problem on 400 grid points at t=0.038, CFL=0.6

Fig.5 Density contours of Shock isentropic wave interaction (shu-osher) problem at t=1.8, N=400, CFL=0.6

Fig.6 Density contours of 2D Riemann problem on 401 × 401 grid points at t=0.8, CFL=0.5 (a) WENO-Z+; (b) WENO-MS-Z+; (c) WENO-Z+M; (d) WENO-MS-Z+M

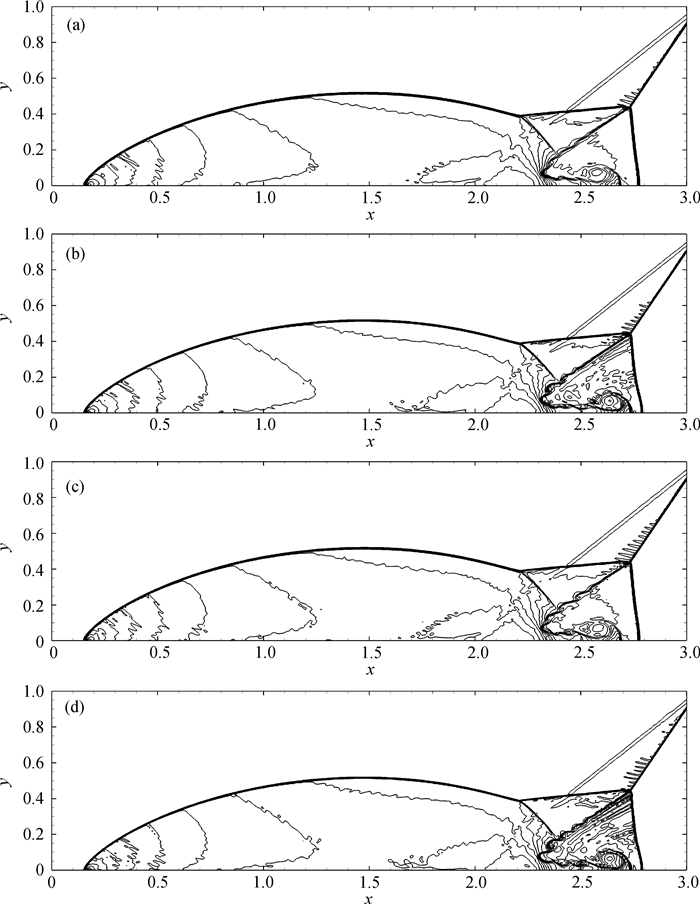
Fig.7 Density contours of double Mach reflection problem on 961 × 241 grid points at t=0.2, CFL=0.5 (a) WENO-Z+; (b) WENO-MS-Z+; (c) WENO-Z+M; (d) WENO-MS-Z+M

References 27

1	LIU XD , OSHER S , CHAN T . Weighted essentially non-oscillatory schemes[J]. Journal of Computational Physics, 1994, 115 (1): 200- 212. DOI
2	HARREN A , ENGQUIST B , OSHER S , et al. Uniformly high-order accurate essentially non-oscillatory schemes Ⅲ[J]. Journal of Computational Physics, 1987, 71 (2): 231- 303. DOI
3	JIANG G S , SHU C W . Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126 (1): 202- 228. DOI
4	HENRICK A K , ASLAM T D , POWERS J M . Mapped weighted essentially non-oscillatory schemes: Achieving optimal order near critical points[J]. Journal of Computational Physics, 2005, 207 (2): 542- 567. DOI
5	BORGES R , CARMONA M , COSTA B , et al. An improved WENO scheme for hyperbolic conservation laws[J]. Journal of Computational Physics, 2008, 227 (6): 3191- 3211. DOI
6	HA Y , KIM C H , LEE Y J , et al. An improved weighted essentially non-oscillatory scheme with a new smoothness indicator[J]. Journal of Computational Physics, 2013, 232 (1): 68- 86. DOI
7	FAN P , SHEN Y Q , TIAN B L , et al. A new smoothness indicator for improving the weighted essentially non-oscillatory scheme[J]. Journal of Computational Physics, 2014, 269 (1): 329- 354.
8	YAN Z G , LIU H Y , MAO M L , et al. New nonlinear weights for improving accuracy and resolution of weighted compact nonlinear scheme[J]. Computers and Fluids, 2016, 127 (1): 226- 240.
9	CHANG H K , YOUNGSOO H , JUNGHO Y . Modified non-linear weights for fifth-order weighted essentially non-oscillatory schemes[J]. Journal of Scientific Computing, 2016, 67 (1): 299- 323. DOI
10	CASTRO M , COSTA B , DON W S . High order weighted essentially non-oscillatory WENO-Z schemes for hyperbolic conservation laws[J]. Journal of Computational Physics, 2011, 230 (5): 1766- 1792. DOI
11	DON W S , BORGES R . Accuracy of the weighted essentially non-oscillatory conservative finite difference schemes[J]. Journal of Computational Physics, 2013, 250 (4): 347- 372.
12	ARANDIGA F , BAEZA A , BELDA A M , et al. Analysis of WENO schemes for full and global accuracy[J]. SIAM Journal on Numerical Analysis, 2011, 49 (2): 893- 915. DOI
13	BORGES R. Recent results on the Improved WENO-Z+ Scheme[M]//Bittencourt M, Dumont N, Hesthaven J, eds. Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2016. Lecture Notes in Computational Science and Engineering, vol 119. Springer, Cham. https://doi.org/10.1007/978-3-319-65870-4_39.
14	WANG Yahui . A 3rd-order modified stencil WENO scheme for solution of hyperbolic conservation law equations[J]. Applied Mathematics and Mechanics, 2022, 43 (2): 224- 236.
15	WANG Y , DU Y , ZHAO K , et al. Modified stencil approximations for fifth-order weighted essentially non-oscillatory schemes[J]. Journal of Scientific Computing, 2019, 81 (2): 898- 922. DOI
16	WANG Y , DU Y , ZHAO K , et al. A new 6th-order WENO scheme with modified stencils[J]. Computers and Fluids, 2020, 208, 104625. DOI
17	ZENG F , SHEN Y , LIU SP . A perturbational weighted essentially non-oscillatory scheme[J]. Computers and Fluids, 2018, 172 (8): 196- 208.
18	GUO Z T , FENG R Z . A high order accuracy corrected hermite-ENO scheme[J]. Chinese Journal of Computational Physics, 2019, 36 (2): 141- 152.
19	GUO Y , TIAN Q , LIANG X , et al. A hybrid WENO scheme for resolution optimization[J]. Chinese Journal of Computational Physics, 2018, 35 (4): 397- 404.
20	ACKER F , BORGES R , COSTA B . An improved WENO-Z scheme[J]. Journal of Computational Physics, 2016, 313 (5): 726- 753.
21	XU W , WU W . An improved third-order WENO-Z scheme[J]. Journal of Scientific Computing, 2018, 75 (3): 1808- 1841. DOI
22	XU W , KONG X , WU W . An improved third-order WENO-Z+3 scheme and its application[J]. Chinese Journal of Computational Physics, 2018, 35 (1): 13- 21.
23	LUO Xin , WU Songping . An improved WENO-Z+ scheme for solving hyperbolic conservation laws[J]. Journal of Computational Physics, 2021, 445, 110608. DOI
24	SHU C W , OSHER S . Efficient implementation of essentially non-oscillatory shock capturing schemes Ⅱ[J]. Journal of Computational Physics, 1989, 83 (3): 32- 78.
25	SOD G . A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws[J]. Journal of Computational Physics, 1978, 27 (1): 1- 31. DOI
26	LAX P D . Weak solutions of nonlinear hyperbolic equations and their numerical computation[J]. Communications on Pure and Applied Mathematics, 1954, 7 (1): 159- 193. DOI
27	WOODWARD P , COLELLA P . The numerical simulation of two-dimensional fluid flow with strong shocks[J]. Journal of Computational Physics, 1984, 54 (1): 447- 465.

[1]	Supei ZHENG, Mangmang JIAN, Jianhu FENG, Mengqing ZHAI. Sign Preserving WENO-AO-type Central Upwind Schemes [J]. Chinese Journal of Computational Physics, 2022, 39(6): 677-686.
[2]	LI Li, LIU Xiaoyan, LI Xinliang, TIAN Baolin, LIANG Xian, HA Jincai. On Statistical Spectral Property of Nonlinear Weights in High Order Schemes [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(2): 127-140.
[3]	GUO Zitao, FENG Renzhong. A High Order Accuracy Corrected Hermite-ENO Scheme [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(2): 141-152.
[4]	ZHAO Fengxiang, PAN Liang, WANG Shuanghu. Weighted Essentially Non-oscillatory Schemes on Unstructured Quadrilateral Meshes [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(5): 525-534.
[5]	CHENG Xiaohan, NIE Yufeng, CAI Li, FENG Jianhu. Entropy Stable Scheme Based on Moving Meshesfor Hyperbolic Conservation Laws [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2017, 34(2): 175-182.
[6]	REN Jiong, FENG Jianhu, LIU Youqiong, LIANG Nan. High Resolution Entropy Consistent Schemes for Hyperbolic Conservation Laws [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2014, 31(5): 539-551.
[7]	TANG Lingyan, SONG Songhe. An Adaptive Multiresolution Scheme for Hyperbolic Conservation Laws [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2014, 31(2): 155-164.
[8]	FENG Tao, YU Xijun, AN Hengbin, CUI Xia, WU Di, LI Zhenzhen. Adaptive Discontinuous Galerkin Method with Lax-Wendroff Type Time Discretization and Three-dimensional Nonconforming Tetrahedral Mesh for Euler Equations [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2013, 30(6): 791-798.
[9]	CHEN Dawei, YU Xijun. RKCVDFEM for One-dimensional Hyperbolic Conservation Laws [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2009, 26(4): 501-509.
[10]	XU Yun, YU Xijun. Adaptive Discontinuous Galerkin Methods for Hyperbolic Conservation Laws [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2009, 26(2): 159-168.
[11]	HU Yanmei, CHEN Jianzhong, FENG Jianhu. A Fifth-order Semi-discrete Central-upwind Scheme for Hyperbolic Conservation Laws [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2008, 25(1): 29-35.
[12]	CHEN Jian-zhong, SHI Zhong-ke. A Third Order Semi-discrete Central-upwind Scheme for Hyperbolic Conservation Laws [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2006, 23(3): 273-280.
[13]	ZHENG Hua-sheng, ZHAO Ning. A High Order Accurate TVD Difference Scheme for Hyperbolic Conservation Laws [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2005, 22(1): 13-18.
[14]	YU Xi-jun, FU Hong-yuan. A TAYLOR-GALERKIN FINITE ELEMENT METHOD FOR HYPERBOLIC CONSERVATION LAWS [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2000, 17(6): 611-618.
[15]	WANG Jian-li, REN Yu-xin, SHEN Meng-yu. THE ANALYSIS OF SEVERAL FLUX SPLITTING SCHEME BASED ON SPLINE INTERPOLATION FINITE VOLUME SCHEME [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2000, 17(4): 421-425.