Fig.1 The spatial and temporal scales for different scientific disciplines

Fig.2 Notation for the system's dynamics

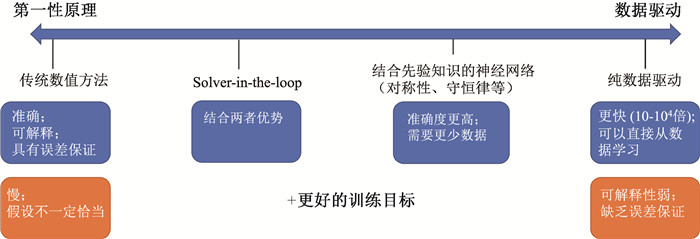
Fig.3 Different simulation methods lying on a spectrum (On the leftmost are classical numerical methods based on first principles. On the rightmost are the pure data-driven methods. Also denoted are the pros and cons for different methods.)

Fig.4 Classical numerical method discretizes the PDE in time and space to facilitate numerically solving them

Fig.5 AI-based simulation method learns a surrogate model fθ and minimizes prediction error

Fig.6 GNS models a physical system as a particle-based system, simulating the temporal dynamics of water (left), sand (middle), and gel (right)[14] (a) prediction results of GNS; (b) after rending

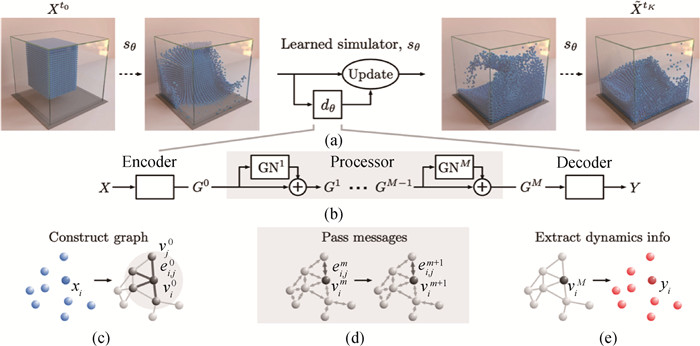
Fig.7 GNS[14] network architecture: The input to the GNS is the state of the system at time t, including every particle's position and velocity. Then through (c) encoder, (d) message passing, and (e) decoder, it predicts the acceleration at time step t+1. Euler's method is used to predict the state at time step t+1.

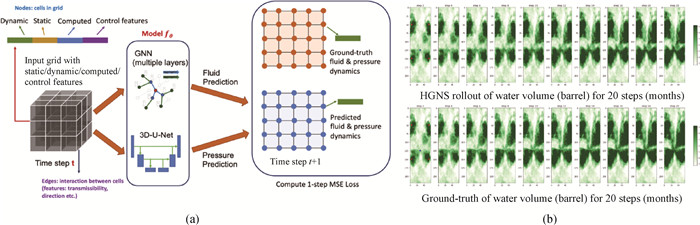
Fig.8 (a) HGNS architecture[15]; (b) its prediction of water volume (cross-section) vs. ground-truth (We see that its prediction matches well with ground-truth.)

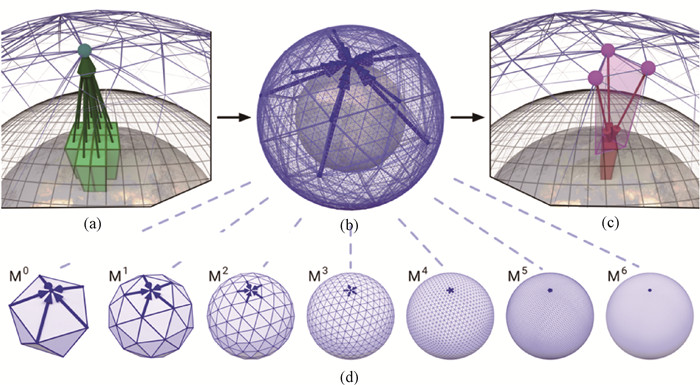
Fig.9 Architecture of GraphCast[16] (Its multiscale graph network can aggregate local and multiscale information.) (a)encoder; (b) processor; (c) decoder; (d) simultaneous multi-mesh message-passing

Fig.10 Neural operator can map an infinite-dimensional function to another infinite dimensional function

Fig.11 Architecture for the Fourier neural operators[26]

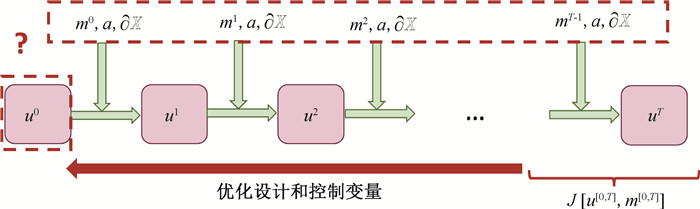
Fig.12 Task setting for scientific design and control (Based on the objective J, it optimizes the initial condition u0, control sequence m[0, T], parameter a or boundary $\partial \mathbb{X} $.)

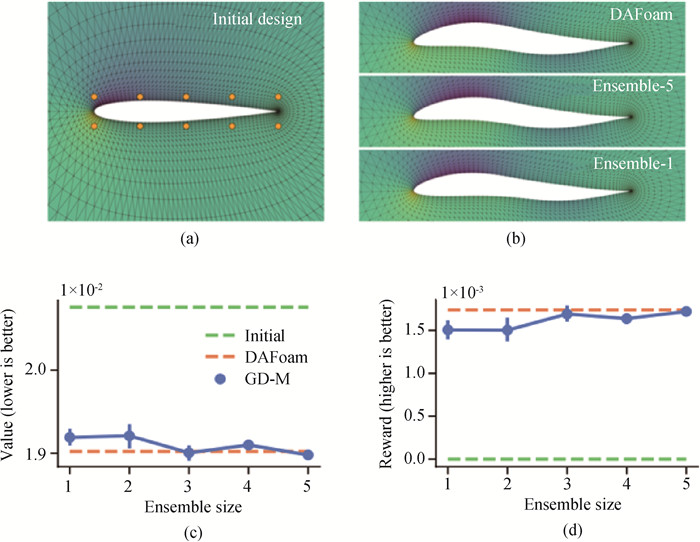
Fig.13 The airfoil design task in Ref.[28], where the design objective is minimizing drag (The surrogate model+backpropagation proposed by the authors attains similar performance as the classical solver (DAFoam), while significantly faster.) (a)initial design; (b) optimized design; (c) drag; (d) reward

Fig.14 Experimental results Ref.[30] (For the inverse problem, if backpropagation is performed in the original space to optimize the initial conditions of the system (first row, without prior), it will obtain adversarial samples with high-frequency noise. On the other hand, if performing optimization in the latent space as introduced in the paper, due to the prior knowledge, it will attain the initial conditions that match well with the ground-truth.)

Fig.15 Task setup for reinforcement learning

Fig.16 Tokamakà configuration variable (TCV) fusion device in Switzerland

Fig.17 Illustration of the interaction between the deep reinforcement learning method[31] and the tokamak device in TCV (a)deployment; (b)TCV; (c)vessel cross section

Fig.18 Illustration of training and inference pipeline[35] (a)train; (b) compositional design

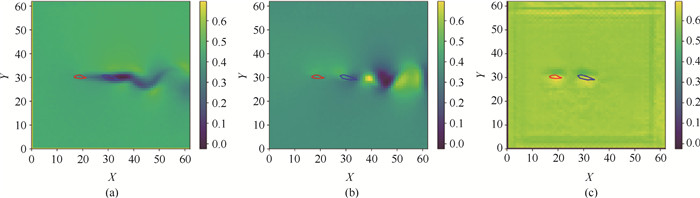
Fig.19 The system's state trajectory and airfoil shape by simultaneously generated[35] (a) horizontal velocity field; (b) vertical velocity field; (c) pressure field. (It also discovers formation flying, which does not appear in training.)

Fig.20 Architecture of (a) AI Feynman and (b) some of its re-discovered equations

Fig.21 Architecture of KAN[54]

Fig.22 Pipeline of AI-descartes[64]