Analysis of Parallel Scalability Bottleneck for Algebraic Multigrid in Typical Real Applications

doi:10.19596/j.cnki.1001-246x.8737

Abstract

Abstract:

Algebraic multigrid (AMG) is an optimal algorithm for solving large-scale sparse linear systems. However, its complexity makes it challenging to achieve ideal parallel scalability and identify parallel scalability bottlenecks. In this paper, we analyze the performance skeletons and communication patterns of the AMG algorithm to identify three categories of scalability bottlenecks. Additionally, we introduce the concept of the sparse matrix communication domain to characterize the influence of sparse patterns on parallel communication performance. We examine six typical examples with varying sparse pattern features in practical applications such as radiation fluid dynamics, structural mechanics, and aero-engines. Through our analysis, we identify and analyze multi-granularity parallel scalability bottlenecks and provide insights into future directions for improving AMG parallel performance.

Key words: algebraic multigrid, parallel preconditioning algorithms, parallel scalability, performance analysis, performance bottleneck

CLC Number:

O246

Runzhang MAO, Hao DU, Hongyun TIAN, Silu HUANG, Peng ZHANG, Xiaowen XU. Analysis of Parallel Scalability Bottleneck for Algebraic Multigrid in Typical Real Applications[J]. Chinese Journal of Computational Physics, 2024, 41(4): 403-417.

Figures/Tables 20

Table 1 Component modules, implications, computational patterns, and communication patterns involved in the AMG algorithm

算法步骤	组件模块	内涵	计算模式^①	通信模式
1.1	Coarsen	选择粗变量集合	图遍历	聚合通信，点对点通信
1.2	BuildInterp	构造插值算子	图遍历	点对点通信
1.3	RAP	三个矩阵相乘	SpGeMM^②	聚合通信、点对点通信
2.1	Smooth	前光滑、后光滑	SpTrSV^③	点对点通信
2.2	Restrict	残差限制	SpMV^④、SpMTV^⑤	点对点通信
2.3	CoarsestSolver	最粗层求解器	LU分解	点对点通信
2.4	Prolong	插值校正	SpMV	点对点通信
2.6	ResidualNorm	计算残差	SpMV、内积	聚合通信、点对点通信

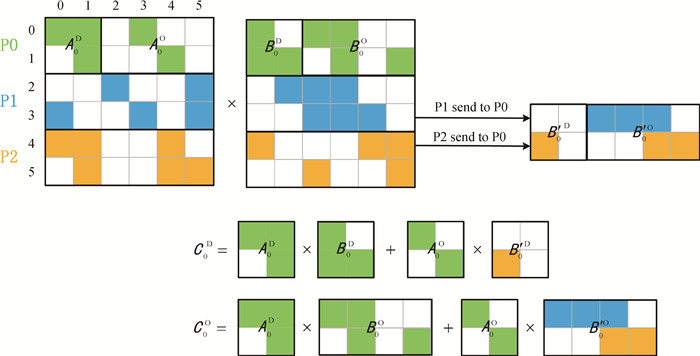
Fig.1 Schematic diagram of point-to-point communication mode for sparse matrix multiplication C=AB (The specific implementation process is demonstrated using process 0 as an example. The sparse matrix A and B is partitioned by rows and assigned to each process. Green, blue, and orange represent the matrix elements owned by processes 0, 1, and 2, respectively.)

Fig.2 Performance skeleton diagram of Setup phase of AMG algorithm

Fig.3 Performance skeleton diagram of Solve phase of AMG algorithm

Table 2 Application background of test examples

算例名	应用领域	偏微分方程	网格类型	离散方法
RHD-1T	辐射流体力学流体不稳定性	三维辐射扩散方程	结构网格	有限体积7点格式
RHD-3T	辐射流体力学流体不稳定性	三维三温能量方程	结构网格	有限体积7点格式
SM-LXJ	离心机装置结构力学分析	三维线弹性方程	非结构网格	有限元
SM-C	接触问题结构力学分析	三维线弹性方程	非结构网格	有限元
HF-S	航空发动机整机静力学分析	三维线弹性方程	非结构网格	有限元
HF-C	航空发动机燃烧室仿真	三维压力方程	非结构网格	有限元

Table 3 Basic algebraic characteristics of test examples

算例名	阶数	非零元数	平均每行非零元数	稠密度	带宽
RHD-1T	2 097 152	14 581 760	6.95	3.32×10^-6	16 384
RHD-3T	6 291 456	52 133 888	8.29	1.32×10^-6	49 152
SM-LXJ	83 073	2 826 927	34.03	4.10×10^-4	45 426
SM-C	12 075 090	655 371 242	54.27	4.49×10^-6	12 075 079
HF-S	2 081 541	71 033 481	34.13	1.63×10^-5	733 683
HF-C	19 637 808	97 535 370	4.97	2.53×10^-7	18 234 897

Fig.4 Matric sparse distribution of test examples (a)RHD-1T; (b)RHD-3T; (c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C

Fig.5 Three types of AMG scalable performance bottlenecks (a) the first type; (b) the second type and (c) the third type

Fig.6 Sparse matrix communication domain diagram (Di represents the communication domain of the i-th process.)

Table 4 Average matrix communication domain of examples at each grid layer (L0 represents the finest grid layer with 2 048 processes.)

网格层	L0	L1	L2	L3	L4	L5	L6	L7
RHD-1T	17.0	48.3	119.2	220.7	309.1	142.4	42.4
RHD-3T	17.0	48.5	120.6	223.1	333.3	174.9	50.4
SM-LXJ	160.2	274.2	275.3	196.3	98.3	38.1	12.2
SM-C	127.4	103.9	107.5	150.6	180.3	25.7
HF-S	189.8	244.1	273.1	272.5	229.9	128.4	38.3	12.5
HF-C	848.9	853.0	860.5	865.4	840.9	599.0	200.7	32.6

Table 5 Test parameters of AMG solver

插值类型	粗化类型	光滑类型	强连通阈值	最粗层矩阵规模阈值
修正的经典插值^[33]	HMIS^[34]	混合对称的Gauss-Seidel^[7]	0.25	100

Fig.7 Time trend chart of four components at Level 1 of the Setup phase (a) time percentage and (b) number of processors

Fig.8 Time trend chart of 4 communication functions in the FIS module of Coarsen component with number of processes (a)RHD-1T; (b)RHD-3T; (c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C

Fig.9 Allreduce time per process under 1 024 processes (a)RHD-1T; (b)RHD-3T;(c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C

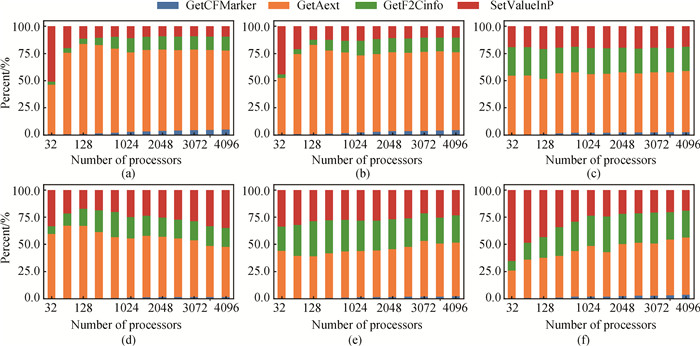
Fig.10 The percentage of time of the four modules in the BuildInterp component with number of processes (a)RHD-1T; (b)RHD-3T; (c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C

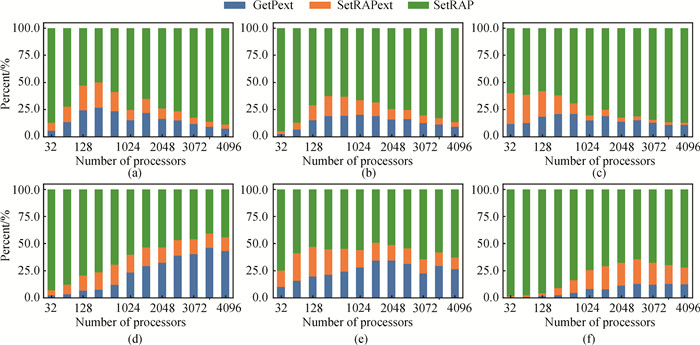
Fig.11 The percentage of time of the three modules in the RAP component with number of processes (a)RHD-1T; (b)RHD-3T; (c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C

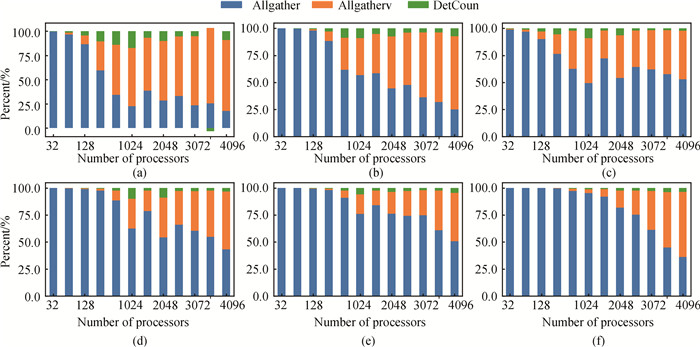
Fig.12 The time percentage of the CPkg module in the RAP component for each example with number of processes (a)RHD-1T; (b)RHD-3T; (c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C

Fig.13 The time percentage of the Cycle module for each example with number of processes (a)RHD-1T; (b)RHD-3T; (c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C

Table 6 Maximum number of non-zero elements per row of interpolation operator for each example at each grid level (L0 represents the finest grid layer and the number of processes is 4 096.)

层号	L0	L1	L2	L3	L4	L5	L6
RHD-1T	6	16	11	8	7	6	42.4
RHD-3T	7	16	12	8	8	6
SM-LXJ	14	20	16	14	14	4
SM-C	12	13	10	7	5	1
HF-S	16	12	10	10	8	8	5
HF-C	4	10	9	9	8	6	5

Fig.14 Radar chart of time percentage for different modules of examples under asymptotic size in each stage (Setup or Solve)

References 35

1	BRANDT A. Multi-Level adaptive techniques (MLAT) for partial differential equations: ideas and software[M]//RICE J R. Mathematical Software. New York: Academic Press, 1977: 277-318.
2	徐小文, 莫则尧, 安恒斌. 求解大规模稀疏线性代数方程组序列的自适应AMG预条件策略[J]. 中国科学: 信息科学, 2016, 46 (10): 1411- 1420.
3	徐小文, 莫则尧, 安恒斌. 求解二维三温辐射扩散方程组的一种代数两层迭代方法[J]. 计算物理, 2009, 26 (1): 1- 8. DOI
4	QIAO Changhe , WU Shuhong , XU Jinchao , et al. Analytical decoupling techniques for fully implicit reservoir simulation[J]. Journal of Computational Physics, 2017, 336, 664- 681. DOI
5	CHEN Junqing , CHEN Zhiming , CUI Tao , et al. An adaptive finite element method for the eddy current model with circuit/field couplings[J]. SIAM Journal on Scientific Computing, 2010, 32 (2): 1020- 1042. DOI
6	周志阳, 徐小文, 舒适, 等. 二维三温辐射扩散方程组两层预条件子的自适应求解[J]. 计算物理, 2012, 29 (4): 475- 483. DOI
7	HENSON V E , YANG U M . BoomerAMG: A parallel algebraic multigrid solver and preconditioner[J]. Applied Numerical Mathematics, 2002, 41 (1): 155- 177. DOI
8	BELL N , OLSON L N , SCHRODER J . PyAMG: Algebraic multigrid solvers in python[J]. Journal of Open Source Software, 2022, 7 (72): 4142. DOI
9	XU Xiaowen , YUE Xiaoqiang , MAO Runzhang , et al. JXPAMG: a parallel algebraic multigrid solver for extreme-scale numerical simulations[J]. CCF Transactions on High Performance Computing, 2023, 5 (1): 72- 83. DOI
10	NAUMOV M , ARSAEV M , CASTONGUAY P , et al. AmgX: A library for GPU accelerated algebraic multigrid and preconditioned iterative methods[J]. SIAM Journal on Scientific Computing, 2015, 37 (5): S602- S626. DOI
11	HÄFNER F. Simulation and parameter identification of Oswald's saltpool experiments with the SAMG multigrid-solver in the transport code MODCALIF[C]//Proceedings of the Conference "Finite-Element Models, MODFLOW, and More", 2004: 13-16.
12	徐小文. 并行代数多重网格算法: 大规模计算应用现状与挑战[J]. 数值计算与计算机应用, 2019, 40 (4): 243- 260.
13	YANG U M. Parallel algebraic multigrid methods-high performance preconditioners[M]//Bruaset A M, Tveito A. Numerical Solution of Partial Differential Equations on Parallel Computers. Berlin: Springer, 2006: 209-236.
14	MO Zeyao , XU Xiaowen . Relaxed RS0 or CLJP coarsening strategy for parallel AMG[J]. Parallel Computing, 2007, 33 (3): 174- 185. DOI
15	GAHVARI H, GROPP W, JORDAN K E, et al. Modeling the performance of an algebraic multigrid cycle using hybrid MPI/OpenMP[C]//2012 41st International Conference on Parallel Processing. Pittsburgh: IEEE, 2012: 128-137.
16	BIENZ A , FALGOUT R D , GROPP W , et al. Reducing parallel communication in algebraic multigrid through sparsification[J]. SIAM Journal on Scientific Computing, 2016, 38 (5): S332- S357. DOI
17	MASCAGNI M , BIENZ A , GROPP W D , et al. Reducing communication in algebraic multigrid with multi-step node aware communication[J]. International Journal of High Performance Computing Applications, 2020, 34 (5): 547- 561. DOI
18	BAKER A H, SCHULZ M, YANG U M. On the performance of an algebraic multigrid solver on multicore clusters[M]//PALMA J M L M, DAYDÉ M, MARQUES O. High Performance Computing for Computational Science-VECPAR 2010. Berlin: Springer, 2010: 102-115.
19	BAKER A H, GAMBLIN T, SCHULZ M, et al. Challenges of scaling algebraic multigrid across modern multicore architectures[C]//2011 IEEE International Parallel & Distributed Processing Symposium. Anchorage: IEEE, 2011: 275-286.
20	PARK J, SMELYANSKIY M, YANG U M, et al. High-performance algebraic multigrid solver optimized for multi-core based distributed parallel systems[C]//Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis. Austin, Texas: Association for Computing Machinery, 2015: 54.
21	BRANNICK J J , FALGOUT R D . Compatible relaxation and coarsening in algebraic multigrid[J]. SIAM Journal on Scientific Computing, 2010, 32 (3): 1393- 1416. DOI
22	徐小文, 莫则尧. 并行代数多重网格算法可扩展性能分析[J]. 计算物理, 2007, 24 (4): 387- 394. DOI
23	徐小文, 莫则尧, 曹小林. HYPRE中多重网格解法器的并行可扩展性能分析[J]. 软件学报, 2009, 20 (Z1): 8- 14.
24	田鸿运. 大规模数值模拟运行时稳定性评测与诊断[D]. 北京: 中国工程物理研究院, 2022.
25	YANG U, FALGOUT R, PARK J. Algebraic Multigrid Benchmark[R]. Livermore, CA (United States): Lawrence Livermore National Lab (LLNL), 2017.
26	FALGOUT R D , JONES J E , YANG U M . Pursuing scalability for hypre's conceptual interfaces[J]. ACM Transactions on Mathematical Software, 2005, 31 (3): 326- 350. DOI
27	PATARASUK P , YUAN Xin . Bandwidth optimal all-reduce algorithms for clusters of workstations[J]. Journal of Parallel and Distributed Computing, 2009, 69 (2): 117- 124. DOI
28	傅天豪, 田鸿运, 金煜阳, 等. 一种面向构件化并行应用程序的性能骨架分析方法[J]. 计算机科学, 2021, 48 (6): 1- 9.
29	ADVE V , SAKELLARIOU R . Application representations for multiparadigm performance modeling of large-scale parallel scientific codes[J]. International Journal of High Performance Computing Applications, 2000, 14 (4): 304- 316. DOI
30	SODHI S, SUBHLOK J. Skeleton based performance prediction on shared networks[C]//IEEE International Symposium on Cluster Computing and the Grid, 2004. CCGrid 2004. Chicago: IEEE, 2004: 723-730.
31	SODHI S , SUBHLOK J , XU Qiang . Performance prediction with skeletons[J]. Cluster Computing, 2008, 11 (2): 151- 165. DOI
32	VETTER J S , MCCRACKEN M O . Statistical scalability analysis of communication operations in distributed applications[J]. ACM SIGPLAN Notices, 2001, 36 (7): 123- 132. DOI
33	DE STERCK H , FALGOUT R D , NOLTING J W , et al. Distance-two interpolation for parallel algebraic multigrid[J]. Numerical Linear Algebra With Applications, 2008, 15 (2/3): 115- 139.
34	DE STERCKH H , YANG U M , HEYS J J . Reducing complexity in parallel algebraic multigrid preconditioners[J]. SIAM Journal on Matrix Analysis and Applications, 2006, 27 (4): 1019- 1039.
35	徐小文, 莫则尧, 武林平. 迭代方法中基于渐近规模的通信与计算比分析[J]. 计算机学报, 2013, 36 (4): 782- 789.

[1]	Shi SHU, Xiaoqiang YUE, Jianmeng HE, Xiaowen XU, Zeyao MO. Feature-driven Parallel Algebraic Multigrid Methods for Multi-group Radiation Diffusion Problems [J]. Chinese Journal of Computational Physics, 2024, 41(1): 87-97.
[2]	Chunsheng FENG, Shizhe LI, Shenghao LIU, Chensong ZHANG, Li ZHAO. Application-oriented Preconditioning of Seepage Mechanics [J]. Chinese Journal of Computational Physics, 2024, 41(1): 98-109.
[3]	Yue HAO, Silu HUANG, Xiaowen XU. Convergence Estimation and Characteristic Analysis of A Two-level Iterative Algorithm for Discretized Three-temperature Energy Linear Systems [J]. Chinese Journal of Computational Physics, 2024, 41(1): 122-130.
[4]	Shaoliang HU, Kailong XU, Ran XU, Zaigang LIU, Xiaowen XU, Hengbin AN, Ronghong FAN, Zhenyu WANG, Wei WANG. A Algebraic Multigrid Algorithm Based on Hybrid Coarsening for Pressure Poisson Equation [J]. Chinese Journal of Computational Physics, 2023, 40(5): 527-534.
[5]	Yi HU, Hengbin AN. Algorithms for Solving Electronic Continuity Equation in Numerical Simulation of Semiconductor Devices [J]. Chinese Journal of Computational Physics, 2023, 40(5): 570-582.
[6]	ZUO Fengli, LIU Xu, ZHANG Baoyin, HU Xiaoyan. Parallel Implementation of Fast Multipole Methods for Three-dimensional Potential Fields on JASMIN [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2013, 30(1): 140-147.
[7]	ZHOU Zhiyang, XU Xiaowen, SHU Shi, FENG Chunsheng, MO Zeyao. An Adaptive Two-level Preconditioner for 2-D 3-T Radiation Diffusion Equations [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2012, 29(4): 475-483.
[8]	CHENG Jie, ZHANG Linbo. A Scalable Parallel Algorithm for Three-dimensional Semiconductor Device Simulation [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2012, 29(3): 439-448.
[9]	XU Xiaowen, MO Zeyao, AN Hengbin. Algebraic Two-level Iterative Method for 2-D 3-T Radiation Diffusion Equations [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2009, 26(1): 1-8.
[10]	XU Xiaowen, MO Zeyao. Scalability Analysis for Parallel Algebraic Multigrid Algorithms [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2007, 24(4): 387-394.
[11]	SHU Shi, HUANG Yun-qing, YANG Ying, YU Xi-jun, XIAO Ying-xiong. A Class of Algebraic Multigrid Algorithms with Three-Dimensional Equal Algebraic Structures [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2005, 22(6): 18-22.
[12]	Mo Zeyao, Xu Linbao, Zhang Baolin, Shen Longjun. Parallel computing and performance analysis for 2-dimensional plasma simulations with particle clouds in cells methods [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1999, 16(5): 496-504.
[13]	Fu Hanqing, Chang Qianshun. Application of Algebraic Multigrid Method to Solve the Splitting Scheme of One-dimensional Euler Equations [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1997, 14(1): 19-25.
[14]	Chang Qianshun, Li Zhengfeng. NEW INTERPOLATION FORMULA IN ALGEBRAIC MULTIGRID METHOD [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 1990, 7(4): 453-460.