三介质Mie-Grüneisen混合模型在水下爆炸防护层问题中的应用

doi:10.19596/j.cnki.1001-246x.8658

摘要/Abstract

摘要：

研究水下爆炸中的防护层问题, 将爆炸气体、水、防护层或其他材料看成一个混合流场后, 它们的物理状态可以直接用统一形式的Mie-Grüneisen状态方程来表示, 再用Mie-Grüneisen混合模型模拟爆炸气体、水、固态防护层之间的复杂相互作用。计算时, 通过状态方程中的特定参数来区分流体成分的物理特性, 并通过体积分数来区分界面, 同时添加自由进出口边界条件; 计算过程中, 对防护层的效果进行细致研究。研究发现, 防护层的效果取决于材料的冲击阻抗。当冲击波从一种介质进入新介质时, 在新介质冲击阻抗较小的情况下其压力会降低。同时, 进入防护层的冲击波被结构物反射又会形成第二个冲击波。在这个过程中, 对防护层的厚度和距离进行关注, 但是这两个因素并未产生重要影响。

关键词: 防护层, 冲击波, Mie-Grüneisen混合模型, 状态方程, 界面

Abstract:

In this paper, our main concern is the effects of the mitigation layer in the underwater explosion problem. As the explosive gaseous products, water, mitigation layer, and so on constitute a fluid mixture, the physical states of these components are covered by a uniform Mie-Grüneisen equation of states(EOS). Then the Mie-Grüneisen mixture model is applied to simulate the complicated interaction among gaseous product, water and solid layer. In the calculation, the particular parameters of EOS are used to make a distinction among the physical properties of fluid components and the volume fractions are used to identify the interfaces. In addition, the inlet and outlet boundary conditions are implemented here. During the calculation process, the effect of the mitigation layer is investigated here. According to the investigation, it is found that the effect of the layer is decided by the shock impedance of layer material. The pressure of the shock wave will decrease when it penetrates a new medium with lower impedance. On the other side, the penetrated shock wave in the layer is reflected by the structure and produces a second shock wave. During this process, the affection of layer thickness and distance is also studied here. But both two factors are unimportant under the mitigation mechanism.

Key words: mitigation layer, shock wave, Mie-Grüneisen mixture model, equation of States, interface

吴宗铎, 满庆洋, 严谨, 庞建华, 孙一方. 三介质Mie-Grüneisen混合模型在水下爆炸防护层问题中的应用[J]. 计算物理, 2023, 40(5): 556-569.

Zongduo WU, Qingyang MAN, Jin YAN, Jianhua PANG, Yifang SUN. Applications of Three-component Mie-GrüNeisen Mixture Model in Underwater Explosion Mitigation Problem[J]. Chinese Journal of Computational Physics, 2023, 40(5): 556-569.

图/表 17

表1 部分材料的Mie-Grüneisen状态参数

Table 1 Mie-Grüneisen state parameters for some materials

	ρ₀/(kg·m^-3)	c₀/(m·s^-1)	s	γ₀	α	适用范围/GPa
水	1 000	1 480	2.560, -1.986, 0.227(s₁, s₂, s₃)	0.5	1.0	0~120
铁(Fe-1018)、钢	7 850	3 574	1.920	1.69	1.0	0~270
聚乙烯塑料	915	2 900	1.481	1.644	1.0	0~50
砂石	1 950	2 450	1.86	1.28	1.0

表2 不同数值模型需要方程数的比较

Table 2 Comparison of equations required in different numerical models

介质数量	多相模型^[33]	五方程模型^[34]	Mie-Grüneisen混合模型
2	7个方程，1个逼近关系式	5个方程，1个逼近关系式	6个方程
3	11个方程，2~3个逼近关系式	7个方程，2~3个逼近关系式	7个方程
4	15个方程，3~6个逼近关系式	9个方程，3~6个逼近关系式	8个方程

图1 TNT-水冲击问题的p、u计算结果

Fig.1 The p、u results of TNT-water impact problem

图2 近壁面气泡问题的压力云图(a) Ref.[36]计算结果；(b) 本文计算结果

Fig.2 Pressure contours of near-wall bubbles problem (a) Ref.[36]'s results; (b) our results

图3 近壁面气泡问题的网格无关性(a) dx=dy=0.007 5；(b) dx=dy=0.003 75

Fig.3 Grid sizes independence in near-wall bubbles problem (a) dx=dy=0.007 5; (b) dx=dy=0.003 75

图4 近壁面气泡问题的时间步无关性(a) CFL=0.6; (b) CFL=0.2

Fig.4 Time step independence in near-wall bubbles problem (a) CFL=0.6; (b) CFL=0.2

图5 正上方固壁处的压力时程曲线

Fig.5 Time evolution of pressure at the rigid body right

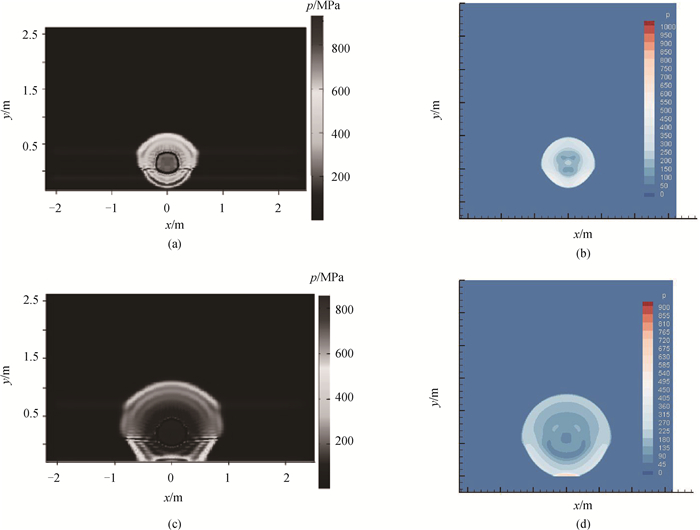
图6 砂石中冲击波反射后的压力分布(a) 0.2 ms时刻Ref.[28]计算结果；(b) 0.2 ms时刻本文计算结果；(c) 0.4 ms时刻Ref.[28]计算结果；(d) 0.4 ms时刻本文计算结果

Fig.6 Pressure distribution of shock wave in sand after reflection (a) Ref.[28]'s results at 0.2 ms; (b) our results at 0.2 ms; (c) Ref.[28]'s results at 0.4 ms; (d) our results at 0.4 ms

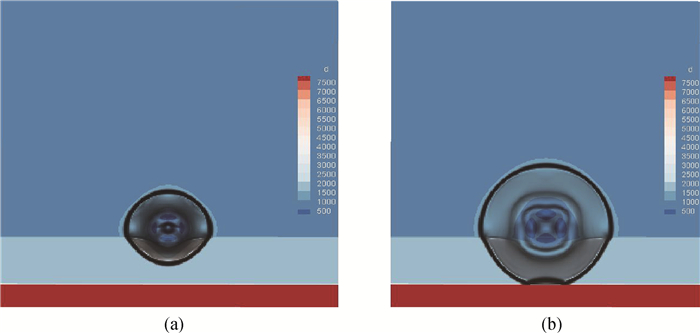
图7 冲击波作用于砂石上不同时刻的密度分布(a) 0.2 ms时刻本文计算结果; (b) 0.4 ms时刻本文计算结果

Fig.7 Density distribution at different time instants with the impact of the shock wave on sand (a) our results at 0.2 ms; (b) our results at 0.4 ms

图8 4种防护情况下压力沿中线x=0的分布

Fig.8 Pressure distribution along the center line x=0.0 for four mitigation cases

图9 4种防护情况下压力时程曲线

Fig.9 Pressure history curves for four mitigation cases

表3 4种介质受冲击阻抗对比

Table 3 The shock impedance contrast of the four mediums under impact

	ρ₀/(kg·m^-3)	冲击波运动时间/ms	冲击波运动距离/m	冲击阻抗SI/(MPa·m·s^-1)
钢铁	7 800	0.138	0.5	28.26
砂石	1 950	0.227	0.5	4.30
聚乙烯塑料(实心)	915	0.139	0.5	3.29
聚乙烯塑料(空心)	750	0.172	0.5	2.33
水	1 000	0.172	0.6~0.075 × 2	2.62

图10 炸药与防护层布置示意图

Fig.10 Schematic diagram of explosive charge and mitigation layer

图11 有无防护层情况下，压力的时程曲线

Fig.11 Pressure history curves whether the mitigation layer exists or not

图12 不同时刻下压力沿中线x=0的分布

Fig.12 Pressure distribution along the center line x=0.0 at different time instants

图13 不同防护层厚度下的压力时程曲线

Fig.13 Pressure history curves for different layer thickness

图14 防护层位置不同时的压力时程曲线

Fig.14 Pressure history curves for different layer positions

参考文献 38

1	COLE R H. Underwater explosion[M]. New Jersey: Princeton University Press, 1948.
2	金泽宇. 抗冲覆盖层水下爆炸计算方法研究[D]. 上海: 上海交通大学, 2017.
3	GLASCOE L, McMICHAEL L, VANDERSALL K, et al. Underwater blast experiments and modeling for shock mitigation[C]. 14th International Detonation Symposium, 2010.
4	贾虎, 沈兆武. 空气隔层对水中冲击波的衰减特性[J]. 爆炸与冲击, 2012, 32(1): 61- 66.
5	YIN C Y, LIU J X, JIN Z Y. Experimental and numerical study of the near-field underwater explosion of a circular plate coated by rigid polyurethane foam[J]. Ocean Engineering, 2022, 252, 111248. DOI
6	YANG G D, FAN Y, WANG G H, et al. Mitigation effects of air-backed RC slabs retrofitted with CFRP subjected to underwater contact explosions[J]. Ocean Engineering, 2023, 267, 113261. DOI
7	AHMED H, HOSAM M, AHMED E, et al. Multi-layer protective armour for underwater shock wave mitigation[J]. Defence Technology, 2015, 11(4): 338- 343. DOI
8	孙远翔, 田俊宏. 近场水下爆炸载荷及舰船结构动态响应研究综述[J]. 舰船科学技术, 2019, 41(11): 1- 8.
9	TAYLOR G I. The pressure and impulse of submarine explosion waves on plates[G]//The Scientific Papers of Sir Georey Ingram Taylor. Cambridge: Cambridge University Press, 1963: 287-303.
10	罗泽立, 周章涛, 毛海斌, 等. 水下爆炸强冲击波与平板结构相互作用的理论分析方法[J]. 高压物理学报, 2017, 31(4): 443- 452.
11	XU L, FENG C L, LIU T G. Analysis of impact load on elastic plate in underwater explosions with modified ghost fluid method[J]. Chinses Journal of Computational Physics, 2017, 34(1): 1- 9.
12	王成, SHUC. 爆炸力学高精度数值模拟研究进展[J]. 科学通报, 2015, 60(10): 882- 898.
13	刘铁钢, 许亮. 模拟多介质界面问题的虚拟流体方法综述[J]. 气体物理, 2019, 4(2): 1- 16.
14	XU L, FENG C L, LIU T G. Design principles of ghost fluid method[J]. Chinses Journal of Computational Physics, 2016, 33(6): 671- 680.
15	ZHAO Z T, RONG J L, ZHANG S X. An interface sharpening technique for the simulation of underwater explosions[J]. Ocean Engineering, 2022, 266, 112922. DOI
16	DING Y, YUAN L, YANG L. An explicit-implicit algorithm for ghost fluid method[J]. Chinese Journal of Computational Physics, 2013, 30(1): 27- 34.
17	姚成宝, 付梅艳, 韩峰, 等. 欧拉坐标系下具有锐利相界面的可压缩多介质流动数值方法研究[J]. 力学学报, 2020, 52(4): 1063- 1079.
18	ZHAO Q, ZHANG M P, XU S L, et al. Numerical simulation of planar moving shock interacting with a single row of water columns and multi-material interfaces[J]. Chinses Journal of Computational Physics, 2018, 35(3): 285- 293.
19	WU W B, LIU Y L, ZHANG A M, et al. An h-adaptive local discontinuous Galerkin method for second order wave equation: Applications for the underwater explosion shock hydrodynamics[J]. Ocean Engineering, 2022, 264, 112526.
20	PENG Y X, ZHANG A M, MING F R. Numerical simulation of structural damage subjected to the near-field underwater explosion based on SPH and RKPM[J]. Ocean Engineering, 2021, 222, 108576.
21	于明. 固体炸药爆轰与惰性介质相互作用的一种扩散界面模型[J]. 爆炸与冲击, 2020, 40(10): 110- 121.
22	FAVRIE N, GAVRILYUK S L, SAUREL R. Solid-fluid diffuse interface model in cases of extreme deformations[J]. Journal of Computational Physics, 2009, 228(16): 6037- 6077.
23	梁姗, 刘伟, 袁礼. 七方程可压缩多相流模型的HLLC格式及应用[J]. 力学学报, 2012, 44(5): 884- 895.
24	WANG Z, ZOU G Y, GONG J, et al. A pressure-based algorithm for numerical simulation of one-dimensional two-phase flow[J]. Chinses Journal of Computational Physics, 2019, 36(4): 413- 420.
25	WU Z D, YAN J, ZONG Z, et al. A diffused interface type mass fraction model with time steps saving mixture rules[J]. Chinses Journal of Computational Physics, 2022, 39(5): 510- 520.
26	XUE C, LI X D, SUN W J, et al. A multi-material five-equation-reduced model and arlificial compression method for interface capture[J]. Chinses Journal of Computational Physics, 2021, 38(3): 257- 268.
27	SHYUE K M. A fluid-mixture type algorithm for compressible multicomponent flow with Mie-Grüneisen equation of state[J]. Journal of Computational Physics, 2001, 171(2): 678- 707.
28	姚熊亮, 陈娟, 张阿漫, 等. 基于SPH方法的二维水下爆炸冲击载荷计算[J]. 哈尔滨工程大学学报, 2010, 31(10): 1303- 1311.
29	MILLER G H, PUCKETT E G. A high-order Godunov method for multiple condensed phases[J]. Journal of Computational Physics, 1996, 128(1): 134- 164.
30	ZHOU J, XU S L. Numerical inlet and outlet boundary conditions in SPH method[J]. Chinses Journal of Computational Physics, 2016, 33(5): 516- 522.
31	LEE E, FINGER M, COLLINS W. JWL equation of state coefficients for high explosives, UCID-16189[R]. Livermore: Lawrence Livermore National Laboratory, 1973.
32	ZHANG B P, ZHANG Q M, HUANG F L. Detonation physics[M]. Beijing: Weapon Industry Press, 2006.
33	SAUREL R, ABGRALL R. A multiphase Godunov method for compressible multifluid and multiphase flows[J]. Journal of Computational Physics, 1999, 150(2): 425- 467.
34	ALLAIRE G, CLERC S, KOKH S. A five-equation model for the simulation of interfaces between compressible fluids[J]. Journal of Computational Physics, 2002, 181(2): 577- 616.
35	REN Y X, CHEN H X. Fundamental computational fuilds dynamics[M]. Beijing: Tsinghua University Press, 2006.
36	XIE W F, YOUNG Y L, LIU T G, et al. Dynamic response of deformable structures subjected to shock load and cavitation reload[J]. Computational Mechanics, 2007, 40(4): 667- 681.
37	高飞, 邱艳宇, 王明洋, 等. 基于孔隙演化的砂土冲击绝热关系研究[J]. 振动与冲击, 2017, 36(17): 134- 140.
38	XU L Y, WANG S P, LIU Y L, et al. Numerical simulation on the whole process of an underwater explosion between a deformable seabed and a free surface[J]. Ocean Engineering, 2021, 219, 108311.

[1]	蔡洪波, 许育培, 姚沛霖, 张恩浩, 黄翰霄, 朱少平, 贺贤土. 混合流体-PIC物理建模及其在激光聚变中的应用[J]. 计算物理, 2023, 40(2): 159-168.
[2]	张文帅, 蔡洪波, 张恩浩, 杜报, 邹士阳, 朱少平. 马赫数对等离子体碰撞冲击波结构的影响———全动理学模拟研究[J]. 计算物理, 2023, 40(2): 199-209.
[3]	颜子翔, 康炜, 张维岩, 贺贤土. 温稠密物质状态方程的路径积分蒙特卡罗方法研究进展[J]. 计算物理, 2023, 40(2): 258-274.
[4]	骆庆群, 李建素. 基于气液混合层的吸附气体稳定性机理[J]. 计算物理, 2021, 38(4): 465-469.
[5]	薛社生, 李守先. 正冲击波后固壁表面颗粒的上升运动[J]. 计算物理, 2021, 38(3): 280-288.
[6]	高媛, 梁腾飞. 气-固界面作用物理模型的确定性实现方法[J]. 计算物理, 2021, 38(2): 183-191.
[7]	牛霄, 倪国喜, 马文铧. 自适应多分辨率方法在反应多相流数值模拟中的应用[J]. 计算物理, 2020, 37(6): 639-652.
[8]	王雪梅, 董斌, 朱子亮, 杨俊升. 聚合物分子与官能化纳米管相互作用及扩散特性的分子动力学模拟[J]. 计算物理, 2020, 37(5): 589-594.
[9]	柴国亮, 苏军伟, 王乐. 一种保持二阶精度的反距离加权空间插值算法[J]. 计算物理, 2020, 37(4): 393-402.
[10]	高辉, 高瑞峰, 姚孟君, 张道旭, 彭澄宇, 张莹. 液滴撞击液膜的流热耦合界面追踪方法数值模拟[J]. 计算物理, 2020, 37(4): 422-430.
[11]	钟振, 张腾, 肖文君. 月海盆地区壳-幔界面补偿地形体积估计的球谐算法[J]. 计算物理, 2020, 37(3): 335-340.
[12]	张其黎, 刘海风, 李琼, 宋红州, 张弓木. 氢状态方程的路径积分蒙特卡罗研究[J]. 计算物理, 2019, 36(4): 379-385.
[13]	姚孟君, 尚文强, 张莹, 高辉, 张道旭, 刘佩尧. 倾斜壁面中Kelvin-Helmholtz不稳定性演化数值分析[J]. 计算物理, 2019, 36(4): 403-412.
[14]	许国良, 朱一萍, 方林, 杜阳, 黄晓明. 密封界面微孔结构的三维分形重构技术与泄漏特性[J]. 计算物理, 2019, 36(4): 440-448.
[15]	娄钦, 臧晨强, 王浩原, 李凌. 微通道内不混溶气液两相二氧化碳界面动力学行为的格子Boltzmann研究[J]. 计算物理, 2019, 36(2): 153-164.