人工智能加速科学仿真、设计、控制和发现

doi:10.19596/j.cnki.1001-246x.9020

摘要/Abstract

摘要：

近年来, 随着AI for science(科学智能)的蓬勃发展, 人工智能与各门学科的交叉融合逐渐成为一个显著的科学研究趋势。但是, AI for science所涉及的范围很广、学科众多, 因此, 将其梳理成一个统一的体系能够更好地为初入领域的研究者导航。本文认为, 尽管每一门学科研究的对象、方法看似千差万别, 但人工智能可以为科学研究提供一套普适的范式和方法, 解决各科学领域内的重要问题。本文将从科学仿真、设计和控制、发现三个方面展开综述, 明确任务设置, 梳理当前的代表性工作, 并通过具体的例子, 阐释人工智能如何为科学研究助力, 以期使读者能够更好应用已有的方法, 或者研究新的方法。

关键词: 人工智能, 科学仿真, 设计, 控制, 科学发现

Abstract:

With the vigorous development of AI for Science in recent years, the integration of artificial intelligence and various scientific disciplines has become a major trend. However, AI for Science covers a wide range and involves many disciplines. Therefore, organizing it into a unified framework will enable better navigation for newcomers to the field. In this article, we posit that although the objects and methods of scientific research seem to be vastly different, AI can provide a universal paradigm and methods for scientific research in the following three aspects: scientific simulation, design and control, and discovery, solving problems in the field. This article will specifically elaborate on the task setting and current representative work. Through specific examples, we will explain how AI can concretely assist scientific research, facilitating researchers to better apply existing methods or develop novel methods.

Key words: artificial intelligence, scientific simulation, design, control, scientific discovery

吴泰霖. 人工智能加速科学仿真、设计、控制和发现[J]. 计算物理, 2025, 42(2): 127-145.

Tailin WU. AI for Accelerating Scientific Simulation, Design, Control, and Discovery[J]. Chinese Journal of Computational Physics, 2025, 42(2): 127-145.

图/表 24

图1 不同科学领域的大致空间尺度和时间尺度

Fig.1 The spatial and temporal scales for different scientific disciplines

图2 系统动力学的描述设置

Fig.2 Notation for the system's dynamics

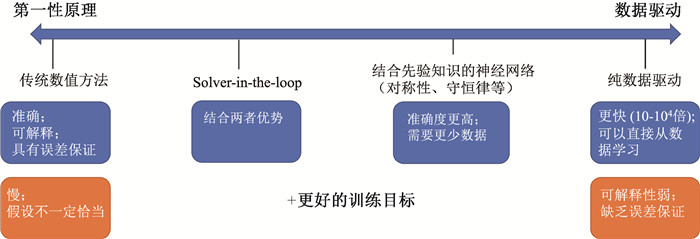
图3 不同仿真方法在光谱上的分布(第一性原理的传统数值方法(最左端)、数据驱动(最右端)以及其优势(蓝色)和局限性(橙色)。)

Fig.3 Different simulation methods lying on a spectrum (On the leftmost are classical numerical methods based on first principles. On the rightmost are the pure data-driven methods. Also denoted are the pros and cons for different methods.)

图4 传统数值方法将偏微分方程在时间和空间上离散化以便于数值求解

Fig.4 Classical numerical method discretizes the PDE in time and space to facilitate numerically solving them

图5 AI仿真模型学习代理模型fθ，最小化预测误差

Fig.5 AI-based simulation method learns a surrogate model fθ and minimizes prediction error

表1 AI仿真模型常用神经网络架构及其优缺点

Table 1 Commonly used neural network architecture of AI simulation model and its advantages and disadvantages

	优点	缺点
GNN (图神经网络)	显示地对对象和它们之间关系建模；适用于描述相互作用复杂、非规则网格等；需要较少的样本	基础的GNN难以对长程影响建模，需要添加多尺度的边
Transformer (变换器架构)	比较适合建模长程关系	参数量较多，需要较多的训练数据
U-Net (U型神经网络)	能够建模规则网格中多尺度的动力学	只能用于规则网格
Neural operator (神经算子)	能够实现超分辨率	大部分只能适用于规则网格，需要较多训练数据

表2 AI仿真模型常用学习范式及其优缺点

Table 2 Common learning paradigms of AI simulation models and their advantages and disadvantages

	优点	缺点
回归	最常用场景	学习的代理模型对于分布外数据泛化性较差；预测效果不会超出所给目标
生成模型	适用于任何回归用的场景，更适合于高维系统，更适合整体、长程的优化	需要一定量的训练数据(但随维度增加，训练数据需要量增加没有回归快)
强化学习	预测效果需要超出所给的目标；在整个环境无法求导时仍可以优化	样本效率较低，需要与环境的大量交互
物理信息	知道系统的控制方程，可以减少样本的需要量	难以泛化到新的边界或者初始条件；系统控制方程不一定准确

图6 GNS将物理系统建模成粒子系统，模拟水流(左)、沙子(中)、胶泥(右)的含时演化[14] (a) GNS预测结果；(b) 经过渲染后的结果

Fig.6 GNS models a physical system as a particle-based system, simulating the temporal dynamics of water (left), sand (middle), and gel (right)[14] (a) prediction results of GNS; (b) after rending

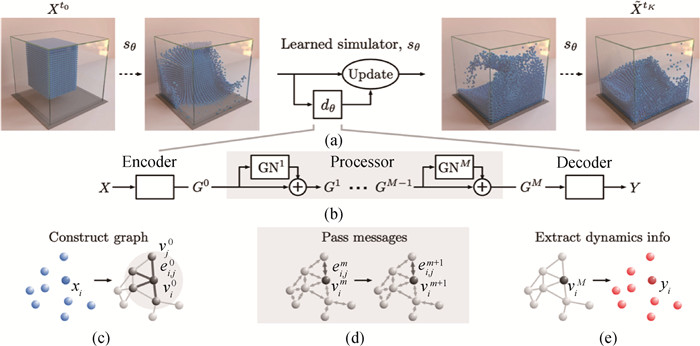
图7 GNS[14]网络架构: 系统在t时刻的状态(各粒子的位置和速度)作为输入，经过(c)编码器, (d)消息传递, (e)解码器，预测t+1时刻的加速度，经过欧拉法预测t+1时刻的系统状态。

Fig.7 GNS[14] network architecture: The input to the GNS is the state of the system at time t, including every particle's position and velocity. Then through (c) encoder, (d) message passing, and (e) decoder, it predicts the acceleration at time step t+1. Euler's method is used to predict the state at time step t+1.

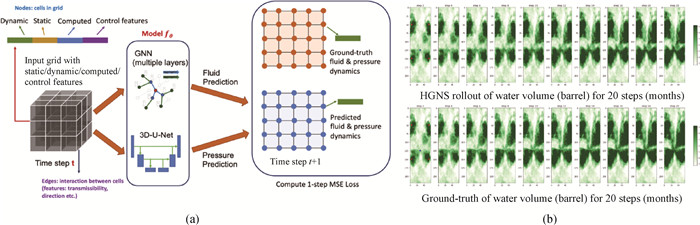
图8 (a) HGNS架构[15]; (b) HGNS对水流体积的预测结果(截面)与真实值比较(可见其在20个月内预测效果与真实值精确符合。)

Fig.8 (a) HGNS architecture[15]; (b) its prediction of water volume (cross-section) vs. ground-truth (We see that its prediction matches well with ground-truth.)

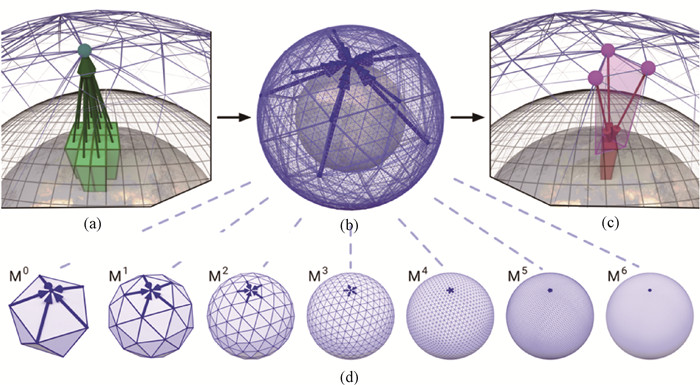
图9 GraphCast架构[16](其构建的多尺度图神经网络，可以同时汇聚局域和多尺度的信息。) (a)encoder; (b) processor; (c) decoder; (d) simultaneous multi-mesh message-passing

Fig.9 Architecture of GraphCast[16] (Its multiscale graph network can aggregate local and multiscale information.) (a)encoder; (b) processor; (c) decoder; (d) simultaneous multi-mesh message-passing

图10 神经算子可以将无限维的函数映射到另一个无限维函数

Fig.10 Neural operator can map an infinite-dimensional function to another infinite dimensional function

图11 傅立叶神经算子[26]的网络架构

Fig.11 Architecture for the Fourier neural operators[26]

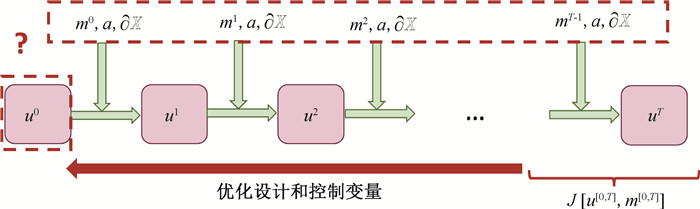
图12 科学设计和控制的任务设置(根据目标J，优化初始条件u0、控制序列m[0, T]、参数a或者边界$\partial \mathbb{X} $。)

Fig.12 Task setting for scientific design and control (Based on the objective J, it optimizes the initial condition u0, control sequence m[0, T], parameter a or boundary $\partial \mathbb{X} $.)

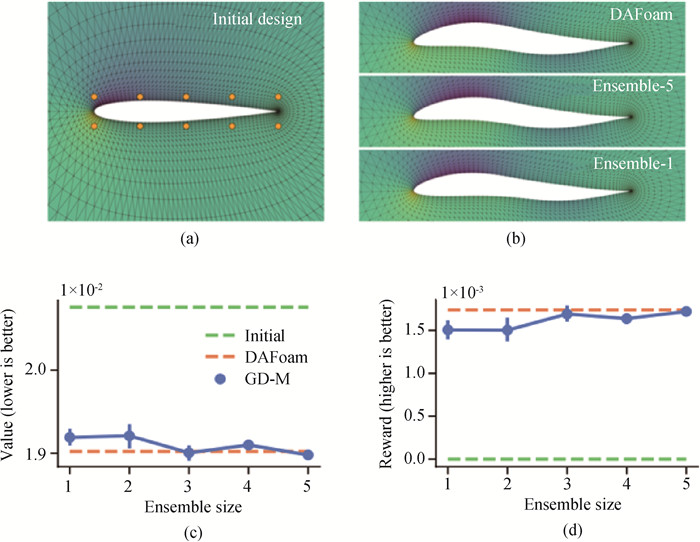
图13 在文[28]对飞机翼型的设计，优化目标为减小阻力(提出的基于代理模型+反向传播的方法达到传统求解器(DAFoam)优化的性能，并且速度更快。)(a)initial design; (b) optimized design; (c) drag; (d)reward

Fig.13 The airfoil design task in Ref.[28], where the design objective is minimizing drag (The surrogate model+backpropagation proposed by the authors attains similar performance as the classical solver (DAFoam), while significantly faster.) (a)initial design; (b) optimized design; (c) drag; (d) reward

图14 文[30]的实验结果(对于逆问题，如果在原空间进行反向传播优化系统初始条件(第一行，without prior)，则会优化出具有高频噪声的对抗样本。而根据文章所提出的在隐空间进行设计，由于有了先验知识，则能优化出与真实值非常一致的初始条件。)

Fig.14 Experimental results Ref.[30] (For the inverse problem, if backpropagation is performed in the original space to optimize the initial conditions of the system (first row, without prior), it will obtain adversarial samples with high-frequency noise. On the other hand, if performing optimization in the latent space as introduced in the paper, due to the prior knowledge, it will attain the initial conditions that match well with the ground-truth.)

图15 强化学习设置

Fig.15 Task setup for reinforcement learning

图16 瑞士的TCV磁约束可控核聚变托卡马克装置

Fig.16 Tokamakà configuration variable (TCV) fusion device in Switzerland

图17 文[31]的深度强化学习与托卡马克装置交互示意图(a)deployment; (b)TCV; (c)vessel cross section

Fig.17 Illustration of the interaction between the deep reinforcement learning method[31] and the tokamak device in TCV (a)deployment; (b)TCV; (c)vessel cross section

图18 文[35]中训练和推理的方法架构(a)训练时；(b)推理时

Fig.18 Illustration of training and inference pipeline[35] (a)train; (b) compositional design

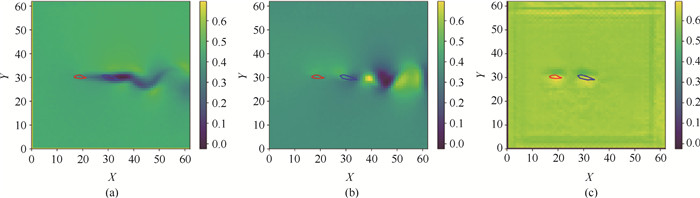
图19 同时生成的系统仿真轨迹和机翼形状[35] (a)气流水平速度场；(b)气流垂直速度场; (c)压强场(中间红色和蓝色表示机翼形状，并发现在训练中未见的“编队飞行”模式。)

Fig.19 The system's state trajectory and airfoil shape by simultaneously generated[35] (a) horizontal velocity field; (b) vertical velocity field; (c) pressure field. (It also discovers formation flying, which does not appear in training.)

图20 (a) AI费曼架构及(b)其重新发现的部分方程

Fig.20 Architecture of (a) AI Feynman and (b) some of its re-discovered equations

图21 KAN架构[54]

Fig.21 Architecture of KAN[54]

图22 AI笛卡尔架构[64]

Fig.22 Pipeline of AI-descartes[64]

参考文献 64

1	WANG Sifan , WANG Hanwen , PERDIKARIS P . Learning the solution operator of parametric partial differential equations with physics-informed DeepONets[J]. Science Advances, 2021, 7 (40): eabi8605. DOI
2	LI Zongyi , ZHENG Hongkai , KOVACHKI N , et al. Physics-informed neural operator for learning partial differential equations[J]. ACM/JMS Journal of Data Science, 2024, 3 (1): 1- 27.
3	SHU Dule , LI Zijie , BARATI FARIMANI A . A physics-informed diffusion model for high-fidelity flow field reconstruction[J]. Journal of Computational Physics, 2023, 478, 111972. DOI
4	UM K, BRAND R, HOLL P, THUEREY N. Solver-in-the-Loop: Learning from differentiable physics to interact with iterative pde-solvers[C]. Thirty-fourth Annual Conference on Neural Information Processing Systems(NeurIPS), Vancouver, Canada, 2022.
5	PESTOURIE R , MROUEH Y , RACKAUCKAS C , et al. Physics-enhanced deep surrogates for partial differential equations[J]. Nature Machine Intelligence, 2023, 12 (5): 1458- 1465.
6	RAO Chengping , REN Pu , WANG Qi , et al. Encoding physics to learn reaction–diffusion processes[J]. Nature Machine Intelligence, 2023, 5 (7): 765- 779. DOI
7	WANG H, LI J, DWIVEDI A, et al. BENO: Boundary-embedded neural operators for elliptic PDEs[C]. The Twelfth International Conference on Learning Representations(ICLR), Vienna, Austria, 2024.
8	SATORRAS V G, HOOGEBOOM E, WELLING M. E(n) equivariant graph neural networks[C]. The Thirty-eighth International Conference on Machine Learning(ICML), 2021.
9	ZHANG Linfeng , HAN Jiequn , WANG Han , et al. Deep potential molecular dynamics: a scalable model with the accuracy of quantum mechanics[J]. Physical Review Letters, 2018, 120 (14): 143001. DOI
10	SCHÜTT K T, KINDERMANS P J, SAUCEDA H E, et al. SchNet: A continuous-filter convolutional neural network for modeling quantum interactions[C]. The Thirty-first Annual Conference on Neural Information Processing Systems(NIPS), Long Beach California USA, 2017.
11	WEILER M, FORRÉ P, VERLINDE E, et al. Coordinate independent convolutional networks——isometry and gauge equivariant convolutions on riemannian manifolds[C]. The Twelfth International Conference on Learning Representations(ICLR), Vienna, Austria, 2024.
12	VILLAR S, HOGG D W, STOREY-FISHER K, et al. Scalars are universal: Equivariant machine learning, structured like classical physics[C]. The Thirty-fifth Annual Conference on Neural Information Processing Systems(NeurIPS), 2021.
13	RAISSI M , PERDIKARI P , KARNIADAKIS G E . Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378, 686- 707. DOI
14	SANCHEZ-GONZALEZ A, GODWIN J, PFAFF T, et al. Learning to simulate complex physics with graph networks[C]. The Thirty-seventh International Conference on Machine Learning(ICML), 2020.
15	WU Tailin, WANG Qinchen, ZHANG Yinan, et al. Learning large-scale subsurface simulations with a hybrid graph network simulator[C]//Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. New York: Association for Computing Machinery, 2020: 4184-4194.
16	LAM R , SANCHEZ-GONZALEZ A , WILLSON M , et al. Learning skillful medium-range global weather forecasting[J]. Science, 2023, 382 (6677): 1416- 1421. DOI
17	PFAFF T, FORTUNATO M, SANCHEZ-GONZALEZ A, et al. Learning mesh-based simulation with graph networks[C]The Ninth International Conference on Learning Representations(ICLR), 2021.
18	WU T, MARUYAMA T, ZHAO Q, et al. Learning controllable adaptive simulation for multi-resolution physics[C]. The Eleventh International Conference on Learning Representations(ICLR), Kigali, Rwanda, 2023.
19	SHLOMI , J , BATTAGLIA P , VLIMANT J R . Graph neural networks in particle physics[J]. Machine Learning: Science and Technology, 2020, 2 (2): 021001.
20	WU Tailin, SUN M, JASON Chou H G, et al. Learning efficient Hybrid particle-continuum Representations of Non-equilibrium N-body systems[EB/OL]. (2023-05-06). https://openreview.net/forum?id=Rd68eTARk4.
21	LI He , WANG Zun , ZOU Nianlong , et al. Deep-learning density functional theory Hamiltonian for efficient ab initio electronic-structure calculation[J]. Nature Computational Science, 2022, 2 (6): 367- 377. DOI
22	XIE T, FU X, GANEA O E, et al. Crystal diffusion variational autoencoder for periodic material generation[C]. The Tenth International Conference on Learning Representations(ICLR), 2022.
23	LI Z, MEIDANI K, YADAV P, FARIMANI A B. Graph neural networks accelerated molecular dynamics[J]. https://arxiv.org/abs/2112.03383,2022.
24	VILLANUEVA-DOMINGO P , VILLAESCUSA-NAVARRO V , ANGLÉS-ALCÁZAR , D , et al. Inferring halo masses with graph neural networks[J]. The Astrophysical Journal, 2022, 935 (1): 30. DOI
25	LI Z, KOVACHKI N, AZIZZADENESHELI K, et al. Fourier neural operator for parametric partial differential equations[C]. The Ninth International Conference on Learning Representations(ICLR), 2021.
26	PATHAK J, SUBRAMANIAN S, HARRINGTON P, et al. FourCastNet: A global data-driven high-resolution weather model using adaptive fourier neural operators[C]. The Eleventh International Conference on Learning Representations(ICLR), Kigali, Rwanda, 2023.
27	WEN Gege , LI Zongyi , LONG Qirrui , et al. Real-time high-resolution CO₂ geological storage prediction using nested Fourier neural operators[J]. Energy & Environmental Science, 2023, 16 (4): 1732- 1741.
28	ALLEN K R, LOPEZ-GUEVARA T, STACHENFELD K, et al. Physical design using differentiable learned simulators[C]. The Twelfth International Conference on Learning Representations(ICLR), Vienna, Austria, 2024.
29	WU Tailin, MARUYAMA T, LESKOVEC J. Learning to accelerate partial differential equations via latent global evolution[EB/OL]. Advances in Neural Information Processing Systems, 2022: 10404055(2022-01-01) [2024-07-25]. https://par.nsf.gov/biblio/10404055-learning-accelerate-partial-differential-equations-via-latent-global-evolution.
30	ZHAO Qingqing, LINDELL D, WETZSTEIN G. Learning to solve PDE-constrained inverse problems with graph networks[C]. International Conference on Machine Learning, PMLR, 2022.
31	DEGRAVE J , FELICI F , BUCHLI J , et al. Magnetic control of tokamak plasmas through deep reinforcement learning[J]. Nature, 2022, 602 (7897): 414- 419. DOI
32	RABAULT J , Ren Feng , Zhang Wei , et al. Deep reinforcement learning in fluid mechanics: A promising method for both active flow control and shape optimization[J]. Journal of Hydrodynamics, 2020, 32, 234- 246. DOI
33	YOU J, LIU B, YING R, et al. Graph convolutional policy network for goal-directed molecular graph generation[C]. The Thirty-second Annual Conference on Neural Information Processing Systems(NeurIPS), Montreal, Canada, 2018.
34	OpenAI team. Video generation models as world simulators[EB/OL]. (2024-02-15) [2024-07-25]. https://openai.com/index/video-generation-models-as-world-simulators/.
35	WU T, MARUYAMA T, WEI L, et al. Compositional generative inverse design[C]. The Twelfth International Conference on Learning Representations(ICLR), Vienna, Austria, 2024.
36	JAN-HENDRIK B , DENNIS M. K . Inverse design of nonlinear mechanical metamaterials via video denoising diffusion models[J]. Nature Machine Intelligence, 2023, 5 (12): 1466- 1475. DOI
37	WEI L, HU P, FENG R, et al. DiffPhyCon: A generative approach to control complex physical systems[C]. The Thirty-eighth Annual Conference on Neural Information Processing Systems(NeurIPS), New Orleans, 2024.
38	WATSON J L , JUERGENS D , BENNETT N R , et al. De novo design of protein structure and function with RFdiffusion[J]. Nature, 2023, 620 (7976): 1089- 1100. DOI
39	ABRAMSON JOSH , ADLER JONAS , DUNGER J , et al. Accurate structure prediction of biomolecular interactions with AlphaFold 3[J]. Nature, 2024, 630, 493- 500. DOI
40	LU Lu , PESTOURIE R , YAO Wenjie , et al. Physics-informed neural networks with hard constraints for inverse design[J]. SIAM Journal on Scientific Computing, 2021, 43 (6): B1105- B1132. DOI
41	YU J, LU Lu, MENG Xuhui, et al. Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems[J]. 2022, 393: 114823.
42	HAO Z, YING C, SU H, et al. Bi-level physics-informed neural networks for PDE constrained optimization using Broyden's hypergradients[C]. The Eleventh International Conference on Learning Representations(ICLR), Kigali, Rwanda, 2023.
43	POKKUNURU A, ROOSHENAS P, STRAUSS T, et al. Improved training of physics-informed neural networks using energy-based priors: A study on electrical impedance tomography[EB/OL]. [2024-07-30]. https://ml4physicalsciences.github.io/2022/files/NeurIPS_ML4PS_2022_92.pdf.
44	MOWLAVI S , NABI S . Optimal control of PDEs using physics-informed neural networks[J]. Journal of Computational Physics, 2023, 473, 111731. DOI
45	BARRY-STRAUME J, SARSHAR A, POPOV A A, et al. Physics-informed neural networks for PDE-constrained optimization and control[DB/OL]. arXiv, 2022: 03377(2022-08-18) [2024-07-30]. https://arxiv.org/abs/2205.03377.
46	MOLINARO R, YANG Y, ENGQUIST B, et al. Neural inverse operators for solving PDE inverse problems[C]. The Fortieth International Conference on Machine Learning(ICML), Honolulu, Hawaii, USA, 2023.
47	LU Lu , JIN Pengzhan , PANG Guofei , et al. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators[J]. Nature Machine Intelligence, 2021, 3 (3): 218- 229. DOI
48	BRUNTON S L , PROCTOR J L , KUTZ J N . Discovering governing equations from data by sparse identification of nonlinear dynamical systems[J]. Proceedings of the National Academy of Sciences of the United States of America, 2016, 113 (15): 3932- 3937.
49	KAHEMAN K , KUTZ J N , BRUNTON S L . SINDy-PI: a robust algorithm for parallel implicit sparse identification of nonlinear dynamics[J]. Proceedings. Mathematical, Physical, and Engineering Sciences, 2020, 476 (2242): 20200279.
50	MESSENGER D A , BORTZ D M . WEAK SINDy: GALERKIN-BASED DATA-DRIVEN MODEL SELECTION[J]. Multiscale Modeling & Simulation, 2021, 19 (3): 1474- 1497.
51	UDRESCU S M , TEGMARK M . AI feynman: a physics-inspired method for symbolic regression[J]. Science Advances, 2020, 6 (16): eaay2631. DOI
52	UDRESCU S M, TAN A, FENG J, et al. AI Feynman 2.0: Pareto-optimal symbolic regression exploiting graph modularity[C]. Thirty-Fourth Annual Conference on Neural Information Processing Systems(NeurIPS), Vancouver, Canada, 2020.
53	LIU Ziming , TEGMARK M . Machine learning hidden symmetries[J]. Physical Review Letters, 2022, 128 (18): 180201. DOI
54	LIU Ziming, WANG Yixuan, VAIDYA S, et al. KAN: Kolmogorov-Arnold Networks[DB/OL]. arXiv, 2024: 19756(2024-04-30) [2024-07-30]. https://arxiv.org/abs/2404.19756.
55	LIU Ziming, MA Pingchuan, WANG Yixuan, et al. KAN 2.0: Kolmogorov-arnold networks meet science[DB/OL]. arXiv, 2024: 10205(2024-08-19) [2024-07-30]. https://arxiv.org/html/2408.10205v1.
56	JIANG Z, WANG C, YANG H. Finite expression methods for discovering physical laws from data[C]. The Twelfth International Conference on Learning Representations(ICLR), Vienna, Austria, 2024.
57	CHEN Yuntian , LUO Yingtao , LIU Qiang , et al. Symbolic genetic algorithm for discovering open-form partial differential equations(SGA-PDE)[J]. Physical Review Research, 2022, 4 (2): 023174. DOI
58	ROMERA-PAREDES R B , BAREKATAIN M , NOVIKOV A , et al. Mathematical discoveries from program search with large language models[J]. Nature, 2024, 625 (7995): 468- 475. DOI
59	TRINH T H , WU Yuhuai , LE Q V , et al. Solving olympiad geometry without human demonstrations[J]. Nature, 2024, 625, 476- 482. DOI
60	BOIKO D A , MACKNIGHT R , Kline B , et al. Autonomous chemical research with large language models[J]. Nature, 2023, 624 (7992): 570- 578.
61	ALFARANO A, CHARTON F, HAYAT A, et al. Global Lyapunov functions: a long-standing open problem in mathematics, with symbolic transformersp[C]. The Twelfth International Conference on Learning Representations(ICLR), Vienna, Austria, 2024.
62	JANSEN P, CÔTÉ M A, KHOT T, et al. DiscoveryWorld: A virtual environment for developing and evaluating automated scientific discovery agents[C]. The Thirty-eighth Annual Conference on Neural Information Processing Systems(NeurIPS), New Orleans, 2024.
63	MAJUMDER B P, TAFJORD O, CLARK P. ScienceAgentBench: Toward rigorous assessment of language agents for data-driven scientific discovery[C]. The Twelfth International Conference on Learning Representations(ICLR), Vienna, Austria, 2024.
64	CORNELIO C , DASH S , AUSTEL V , et al. Combining data and theory for derivable scientific discovery with AI-Descartes[J]. Nature Communications, 2023, 14 (1): 1777.

[1]	徐昌恒, 潘晖, 何明涛, 赵常有, 蔡德昌, 许怀金. 液态重金属反应堆燃料棒及控制棒设计[J]. 计算物理, 2024, 41(5): 582-588.
[2]	韩文敏, 戴耀东, 姚初清, 田家祥, 蒋丹枫, 周一帆. 遗传算法在中子-γ混合辐射场屏蔽材料优化设计中的应用[J]. 计算物理, 2024, 41(3): 357-366.
[3]	李震波, 唐叶芝. 高维混沌系统的多元函数投影同步及其保密通信方案[J]. 计算物理, 2023, 40(1): 91-105.
[4]	陈绍英, 王雪丽, 高志梅, 袁国勇. 环域反馈下复Ginzburg-Landau系统的螺旋波动力学行为[J]. 计算物理, 2022, 39(1): 118-126.
[5]	白婧, 黄志精, 唐国宁. 用运动控制器来终止心律失常[J]. 计算物理, 2021, 38(3): 352-360.
[6]	朱俏俐, 张文欢. 带外力项的iDdQ(q-1)多松弛格子Boltzmann模型[J]. 计算物理, 2020, 37(5): 551-561.
[7]	陈永彬, 唐智礼, 盛建达. 跨音速自然层流翼型多目标优化设计[J]. 计算物理, 2016, 33(3): 283-296.
[8]	周云龙, 徐超. 基于状态反馈控制的无线网络拥塞控制流体流模型的Hopf分岔[J]. 计算物理, 2015, 32(3): 352-360.
[9]	孙静静, 黄朝琴, 姚军, 李爱芬, 王代刚. 基于离散裂缝模型的低渗透油藏开发数值模拟[J]. 计算物理, 2015, 32(2): 177-185.
[10]	陈金繁, 罗超, 敖冰云, 彭丽霞, 石洁. V-Ta合金力学行为的计算与实验研究[J]. 计算物理, 2014, 31(5): 609-616.
[11]	杨翠云, 刘海英, 唐国宁. 两阶段脉冲控制螺旋波的数值模拟[J]. 计算物理, 2014, 31(5): 625-630.
[12]	李欣, 吴畅书, 邹士阳, 赵益清, 李敬宏, 古培俊, 郑无敌, 裴文兵. 点火黑腔二维模拟设计[J]. 计算物理, 2013, 30(3): 371-378.
[13]	李盼池, 王琪超, 施光尧. 基于Bloch球面搜索的量子粒子群优化算法[J]. 计算物理, 2013, 30(3): 454-462.
[14]	陈国荣, 许文涛, 杨昀, 李凯. 含冷却水管大体积混凝土温度场计算的一种新方法[J]. 计算物理, 2012, 29(3): 411-416.
[15]	秦华, 万云芳, 张伟元, 宋延松. 用粒子群算法进行单个非球面透镜的球差校正[J]. 计算物理, 2012, 29(3): 426-432.