过刊目录

1988年, 第5卷, 第4期
刊出日期：1988-12-25 上一期    下一期
---
论文   

全全选选:

导出引用 EndNote Ris BibTeX

隐藏/显示图片

论文

Select

一维非定常炸轰的特征线方法数值模拟 王子修, 李华 1988, 5(4): 383-393.  摘要 ( )   PDF(603KB) ( )   本文用特征线方法计算了一维非定常炸轰的发展和传播问题。为模拟炸药的化学反应,采用了一种冲击波引爆的唯象模型。以PBX-9404高级炸药为例给出了计算的POP图与实验结果的比较以及不同时刻波后流场的分布。

Select

使用改进的有限分析解方法模拟流体分离流动 姜宗林 1988, 5(4): 394-402.  摘要 ( )   PDF(547KB) ( )   在这篇文章里,我们提出了一种改进的有限分析解算法,它能够避免复杂的指数运算和级量求和,节省大量的计算时间,并能在同样的网格尺寸条件下,具有模拟比原算法高20倍以上雷诺数的流体流动问题的能力。对分离流的数值实验表明:对同样的雷诺数,这种算法能得到和原算法非常一致的计算结果。而高雷诺数下的数值结果也是令人满意的。

Select

高能入射电子与原子离子碰撞激发截面 方泉玉, 纪文贵, 蔡蔚, 丘玉波 1988, 5(4): 403-419.  摘要 ( )   PDF(867KB) ( )   本文采用玻恩近似,计算高能入射电子与原子(离子)碰撞激发截面。其中仔细处理了包括复杂原子在内的跃迁矩阵元角部分,因而可以作广泛计算。本文还将计算所得结果与其他方法作了比较,其符合程度一般是相当好的。

Select

铸件在凝固过程中的传热和自然对流计算 赵勇, 刘庄 1988, 5(4): 420-429.  摘要 ( )   PDF(688KB) ( )   论文中以流函数、涡度和温度为基本变量,建立了铸件凝固时的传热和自然对流的数学模型。控制方程采用半隐式有限差分在固定网格上求解。在模型建立过程中,着重讨论了潜热的处理和固液相区(界面)速度条件。对于潜热处理,采用了基于合金平衡相图的比热焓法;对于固液相区(界面)速度条件,提出了一种新的、基于固相率进行修正的处理方法。另外还探讨了将本文提出的解法应用于复杂几何条件的可能性。最后,通过对一个典型例子进行计算,对自然对流对铸件凝固的影响作了深入的讨论。

Select

均匀湍流中的奇怪吸引子 酆庆增, 顾志福, 陈为炎 1988, 5(4): 430-436.  摘要 ( )   PDF(481KB) ( )   本文对于实测的湍流信号采用延迟坐标重建相空间技术计算了它的关联维数,熵和最大Лялнов指数,从而指出这是一种受随机噪声干扰的确定性的混沌现象,它在相空间的吸引子是一个随机噪声背景上的奇怪吸引子。

Select

原子间(锂-锂,氟-氟)位能曲线的ab initio计算 崔作林, 潘守甫 1988, 5(4): 437-442.  摘要 ( )   PDF(360KB) ( )   使用先进的量子化学ab initio程序MONSTERGAUSS和各种基函数组,在较大的核间距内计算了锂-锂,氟-氟原子间的位能曲线。并采用组态相互作用(CI)方法计算了基态锂分子(Li2 1∑g+)和基态氟分子(F2 1∑g+)的平衡核间距及总能量。计算结果与其它理论和实验结果进行了比较。

Select

一种最优控制数值计算方法 张锁春 1988, 5(4): 443-454.  摘要 ( )   PDF(628KB) ( )   本文为解决非线性微分方程自治系统的周期轨道的数值计算,提出了一种最优控制的数值计算方法。其方法的实质是利用连续的打靶法,在非线性最小二乘公式的监护下,附加惩罚函数进行控制来实现的。并利用该法计算了典型的化学反应模型。

Select

超几何方程的解在函数展开中的应用 朱嘉麟 1988, 5(4): 455-465.  摘要 ( )   PDF(543KB) ( )   本文应用超几何方程在正则奇点邻域的解得到各种与超几何函数石关的函数在该邻域的展开式。对第一、二类完全椭圆积分不仅给出展开形式,而且列举了数值计算结果。

Select

重分网格技巧初探 周连胜, 贝新源, 张志杰 1988, 5(4): 466-472.  摘要 ( )   PDF(439KB) ( )   本文讨论按等距原则重新划分拉氏网格的技巧,应用重分阈值η和四步重分方法。新、旧网格之间,按体积份额守恒地分配有关网格量,数值试验表明,为了提高重分效果,不仅需要调整重分区域内部网格点的位置,而且还要适当调整边界网格点的位置。

Select

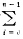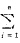一个高精度数值积分公式 吴新元 1988, 5(4): 473-477.  摘要 ( )   PDF(261KB) ( )   本文讨论了一个具有高精度的求积公式∫abf(x)dx)=(b-a)(7f(a)+16f((a+b)/(2))+7f(b)+(b-a)(f'(a)-f'(b)))/30+E[f]其中E[f]=((b-a)7/(604800))f(6)(ξ),a<ξ<b及其复合公式∫ab(f(x)dx)=(b-a)((7f(a+2ih)+7f(a+2ih)+16???19880410-2???f(a+2i-1h)+(b-a)(f'(a)-f(b))/2n)/30n+En[f]这里En[f]=((b-a)7)/(604800n6)f(6)(η),a< η< b而h=(b-a)/2n它具有辛普生公式的一切优点,但精确度比辛普公式高2阶。数值试验表明,这是一个非常有效的求积公式。

Select

高阶有限单元边界积分方法 姜瑜, 郭宽良 1988, 5(4): 478-483.  摘要 ( )   PDF(298KB) ( )   本文在文献[1]的基础上,将高阶元引入边界积分方程方法,对导热问题的求解作了详细说明,给出了几个算例。并在精度上与线性元做了比较。

Select

用A238U超核聚变检验裂变机制的可行性探讨 郑国桐, 陈炽庆, 裘志洪 1988, 5(4): 484-492.  摘要 ( )   PDF(510KB) ( )   超核A238U的裂变的剪断过程,用不断上升的势垒模拟,对不同的剪断过程(恒速或加速),对A末态激发几率(布居于轻裂块的几率)作了计算,分别为27%或31%。有待实验检验。

Select

冷锭在均热炉加热过程中传热的数值计算方法 陈柏润 1988, 5(4): 493-500.  摘要 ( )   PDF(465KB) ( )   本文在[1]基础上,进一步导出冷钢锭在初轧厂均热炉加热过程圆筒模型的数值解法。本方法已成功地应用于攀钢初轧厂的均热炉计算机控制系统中。

Select

定态对流扩散方程的渐近数值方法 吴启光 1988, 5(4): 501-506.  摘要 ( )   PDF(318KB) ( )   本文提出了一种求解定态对流扩散方程的渐近数值方法,在边界层附近不必取很细的网格,对模型问题的数值计算表明,利用中等大小的步长就可得到边界层内的数值解。