Chinese Journal of Computational Physics ›› 2024, Vol. 41 ›› Issue (5): 547-558.DOI: 10.19596/j.cnki.1001-246x.8855
• Special Column on the National Conference on Computational Physics • Previous Articles Next Articles
Kun WANG1( ), Jun CHEN2, Pei WANG2, Wenjun HU3, Zheng ZHONG1
), Jun CHEN2, Pei WANG2, Wenjun HU3, Zheng ZHONG1
Received:2023-10-30
Online:2024-09-25
Published:2024-09-14
CLC Number:
Kun WANG, Jun CHEN, Pei WANG, Wenjun HU, Zheng ZHONG. Fast Complex-amplitude Expanded Phase Field Crystal Model for Different Crystals through a Ginzburg-Landau Approach[J]. Chinese Journal of Computational Physics, 2024, 41(5): 547-558.
Add to citation manager EndNote|Ris|BibTeX
URL: http://www.cjcp.org.cn/EN/10.19596/j.cnki.1001-246x.8855
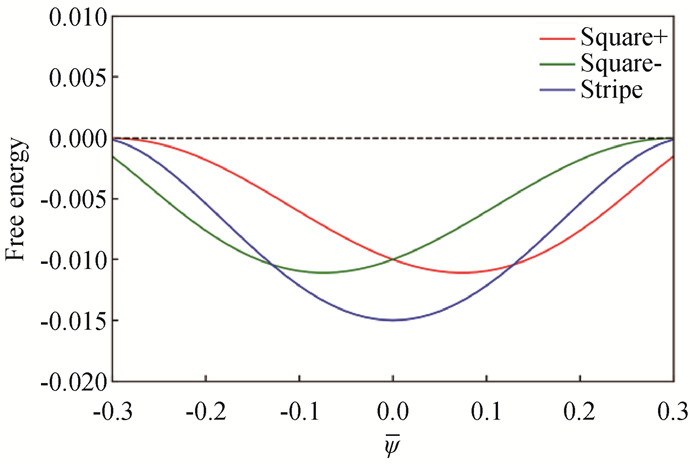
Fig.1 Δfsqmin and Δfstrmin as function of ψ for ω4=λ/2 Square+ and square-correspond to the positive and negative sign adopted in Eq. (18), respectively.
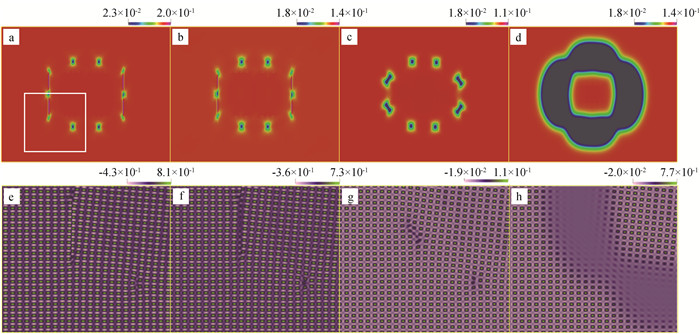
Fig.3 A circular grain embedding in a otherwise perfect rectangular matrix simulated by the fast APFC model with (a) ψ=0.1; (b) ψ=0.2; (c) ψ=0.3; (d) ψ=0.4, respectively. The field plotted is A2. The figure (e)-(f) is the corresponding reconstructed atom number density field of (a)-(d) from the same region which is specially illustrated in (a) by the white solid square (Other model parameters are ε=0.3, g=0, λ=3.0, $\stackrel{◆}{\omega}_4 $=2.1λ, A0=0.2, b=1.25, χani=1.0 and κ=0.0. The structure in (e) and (f) is apparently different from that of (g) and (h), which is a new phase, referred to as the orthogonal layered (OL) phase in this work. In the figure (d) or (h), the liquid phase begins to grow at the grain boundary.)
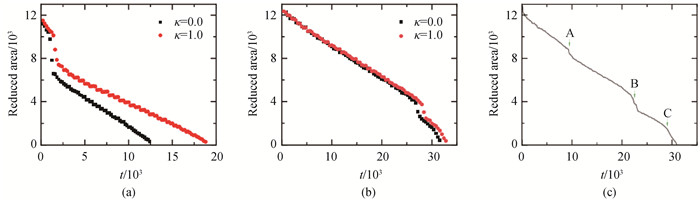
Fig.4 Area of the circular grain versus time calculated by the fast APFC model for (a) hexagonal lattice; (b) square lattice and (c) rectangular lattice (For the rectangular lattice, the grain area is estimated by ra× rb, ra (rb) is the long (short) axis of the elliptical grain. For the other two lattices, the grain area is estimated by the square of the radius of the circular grain. In (c), the three knees corresponding to the change of the shrinking rate are marked by A, B and C.)
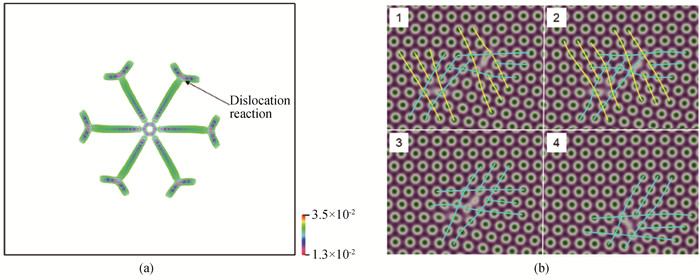
Fig.5 (a) The trajectory of the dislocations of the circular grain in the hexagonal matrix, where the color is encoded by A2; (b) atom number density evolution reconstructed from the position as pointed by the arrow in the figure (a) ((b) 1-4 correspond to the moment of 600, 800, 1 000 and 1 200, where the mixed dislocation cores with different burgers vectors are depicted by the yellow and cyan lines mark. Specially, the [${\rm{\bar 1}}$2${\rm{\bar 1}}$0] dislocation components depicted by the yellow lines in the figure 1 or 2 of (b) cancel out after the dislocation reaction.)
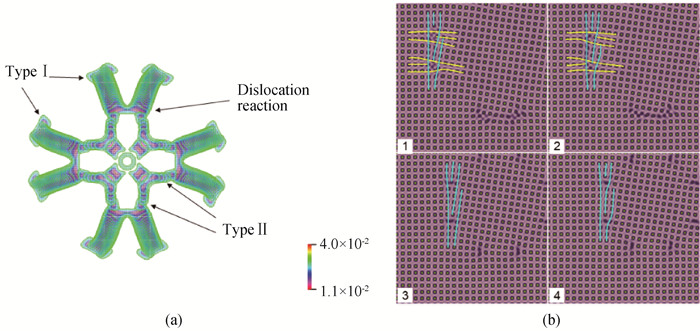
Fig.6 (a) The trajectory of the dislocations of the circular grain in the square matrix, where the color is encoded by A2; (b) Atom number density evolution reconstructed from the position as pointed by the arrow in the figure (a)((b) 1-4 correspond to the moment of 260 000, 268 000, 272 000 and 276 000, where the dislocation cores with different burgers vectors are depicted by the yellow and cyan lines mark. Specially, the <01> dislocation components with the opposite sign depicted by the yellow lines in 1 and 2 of (b) cancel out after the dislocation reaction.)
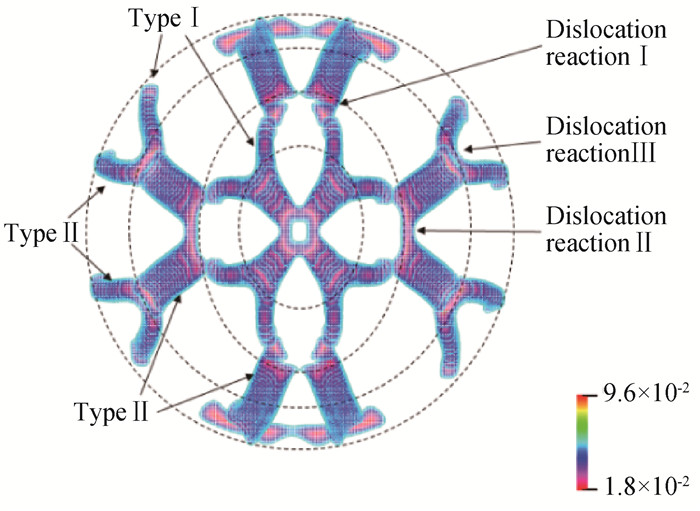
Fig.7 The trajectory and shape of the dislocations of the circular grain in the rectangular matrix (Where the color is encoded by A2.Dislocation cores on the same dashed circle corresponds to the same moment.)
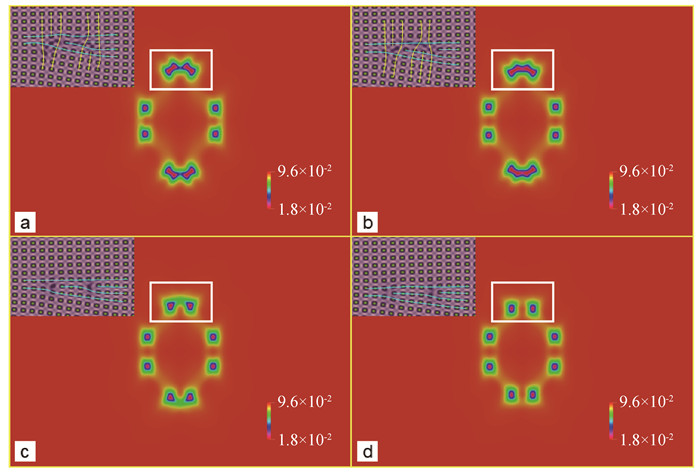
Fig.8 (a) A2 field of dislocation reaction Ⅱ, figure (a)-(d) correspond to the moment of 22 400, 22 800, 2 3000 and 23 200, respectively (The inset shows the reconstructed atom number density from the region marked by the white solid square. The yellow and cyan lines depict the <10> and <01> dislocation, respectively.)
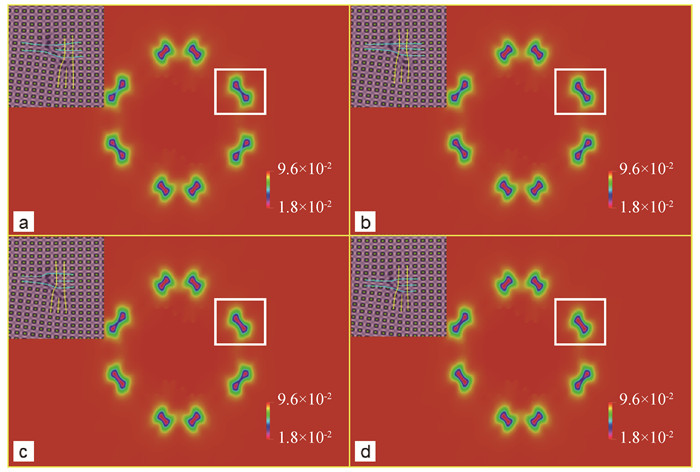
Fig.9 A2 field of dislocation reaction Ⅲ, figure (a)-(d) correspond to the moment of 8 000, 8 300, 8 500 and 8 700, respectively (Other conventions are the same as that of Fig. 8.)
| 1 |
ELDER K R , KATAKOWSKI M , HAATAJA M , et al. Modeling elasticity in crystal growth[J]. Physical Review Letters, 2002, 88 (24): 245701.
DOI |
| 2 | ATHREYA B P , GOLDENFELD N , DANTZIG J A . Renormalization-group theory for the phase-field crystal equation[J]. Physical Review E, 2006, 74 (1): 011601. |
| 3 | GOLDENFELD N , ATHREYA B P , DANTZIG J A . Renormalization group approach to multiscale simulation of polycrystalline materials using the phase field crystal model[J]. Physical Review, 2005, 72 (2): 020601. |
| 4 |
ELDER K R , PROVATAS N , BERRY J , et al. Phase-field crystal modeling and classical density functional theory of freezing[J]. Physical Review B, 2007, 75 (6): 064107.
DOI |
| 5 |
SKAUGEN A , ANGHELUTA L , VINALS J . Dislocation dynamics and crystal plasticity in the phase-field crystal model[J]. Physical Review B, 2018, 97 (5): 054113.
DOI |
| 6 |
SALVALAGLIO M , VOIGT A , ELDER K R . Closing the gap between atomic-scale lattice deformations and continuum elasticity[J]. Npj Computational Materials, 2019, 5, 48.
DOI |
| 7 |
AINSWORTH M , MAO Zhiping . Phase field crystal based prediction of temperature and density dependence of elastic constants through a structural phase transition[J]. Physical Review B, 2019, 100 (10): 104101.
DOI |
| 8 |
SALVALAGLIO M , BACKOFEN R , ELDER K R , et al. Defects at grain boundaries: A coarse-grained, three-dimensional description by the amplitude expansion of the phase-field crystal model[J]. Physical Review Materials, 2018, 2 (5): 053804.
DOI |
| 9 | SALVALAGLIO M , BACKOFEN R , VOIGT A , et al. Controlling the energy of defects and interfaces in the amplitude expansion of the phase-field crystal model[J]. Physical Review E, 2017, 96 (2/1): 023301. |
| 10 |
YAMANAKA A , MCREYNOLDS K , VOORHEES P W . Phase field crystal simulation of grain boundary motion, grain rotation and dislocation reactions in a BCC bicrystal[J]. Acta Materialia, 2017, 133, 160- 171.
DOI |
| 11 |
TARP J M , ANGHELUTA L , MATHIESEN J , et al. Intermittent dislocation density fluctuations in crystal plasticity from a phase-field crystal model[J]. Physical Review Letters, 2014, 113 (26): 265503.
DOI |
| 12 |
CHAN P Y , TSEKENIS G , DANTZIG J , et al. Plasticity and dislocation dynamics in a phase field crystal model[J]. Physical Review Letters, 2010, 105 (1): 015502.
DOI |
| 13 |
HU Nengwen , HUANG Yongfeng , WANG Kun , et al. Roles of triple and quadruple junctions on plasticity by phase-field crystal approach[J]. Physica B: Condensed Matter, 2022, 626, 413449.
DOI |
| 14 |
ZHOU Wenquan , WANG Jincheng , LIN Bo , et al. Yielding and jerky plasticity of tilt grain boundaries in high-temperature graphene[J]. Carbon, 2019, 153, 242- 256.
DOI |
| 15 |
GAO Yingjun , DENG Qianqian , QUAN Silong , et al. Phase field crystal simulation of grain boundary movement and dislocation reaction[J]. Frontiers of Materials Science, 2014, 8 (2): 176- 184.
DOI |
| 16 |
HIROUCHI T , TAKAKI T , TOMITA Y . Effects of temperature and grain size on phase-field-crystal deformation simulation[J]. International Journal of Mechanical Sciences, 2010, 52 (2): 309- 319.
DOI |
| 17 |
STEFANOVIC P , HAATAJA M , PROVATAS N . Phase field crystal study of deformation and plasticity in nanocrystalline materials[J]. Physical Review. E, 2009, 80 (4): 046107.
DOI |
| 18 |
HIROUCHI T , TAKAKI T , TOMITA Y . Development of numerical scheme for phase field crystal deformation simulation[J]. Computational Materials Science, 2009, 44 (4): 1192- 1197.
DOI |
| 19 |
WANG Kun , ZHANG Fengguo , HE Anmin , et al. Plasticity and phase transition of crystals under continuous deformations by phase field crystal approach[J]. International Journal of Plasticity, 2019, 122, 225- 243.
DOI |
| 20 |
SKOGVOLL V , SKAUGEN A , ANGHELUTA L , et al. Dislocation nucleation in the phase-field crystal model[J]. Physical Review B, 2021, 103 (1): 014107.
DOI |
| 21 |
SKOGVOLL V , ANGHELUTA L , SKAUGEN A , et al. A phase field crystal theory of the kinematics of dislocation lines[J]. Journal of the Mechanics and Physics of Solids, 2022, 166, 104932.
DOI |
| 22 |
WANG Kun , XIAO Shifang , CHEN Jun , et al. Exploring atomic mechanisms of microstructure evolutions in crystals under vacancy super-or undersaturation states by a kinetic amplitude-expanded phase-field-crystal approach[J]. International Journal of Plasticity, 2022, 157, 103386.
DOI |
| 23 |
MKHONTA S K , ELDER K R , HUANG Z F . Exploring the complex world of two-dimensional ordering with three modes[J]. Physical Review Letters, 2013, 111 (3): 035501.
DOI |
| 24 | WU K , PLAPP M , VOORHEES P W . Controlling crystal symmetries in phase-field crystal models[J]. Journal of Physics, 2010, 22 (36): 364102. |
| 25 | WU Kuoan , ADLAND A , KARMA A . Phase-field-crystal model for fcc ordering[J]. Physical Review E, 2010, 81 (6): 061601. |
| 26 |
GREENWOOD M , OFORI-OPOKU N , ROTTLER J , et al. Modeling structural transformations in binary alloys with phase field crystals[J]. Physical Review B, 2011, 84 (6): 064104.
DOI |
| 27 |
GREENWOOD M , PROVATAS N , ROTTLER J . Free energy functionals for efficient phase field crystal modeling of structural phase transformations[J]. Physical Review Letters, 2010, 105 (4): 045702.
DOI |
| 28 |
WU Kuoan , LIN Shangchun , KARMA A . Two-mode Ginzburg-Landau theory of crystalline anisotropy for fcc-liquid interfaces[J]. Physical Review B, 2016, 93 (5): 054114.
DOI |
| 29 |
WU Kuoan , KARMA A . Phase-field crystal modeling of equilibrium bcc-liquid interfaces[J]. Physical Review B, 2007, 76 (18): 184107.
DOI |
| 30 |
WU Kuoan , KARMA A , HOYT J J , et al. Ginzburg-Landau theory of crystalline anisotropy for bcc-liquid interfaces[J]. Physical Review B, 2006, 73 (9): 094101.
DOI |
| 31 |
SHIH W H , WANG Z Q , ZENG X C , et al. Ginzburg-Landau theory for the solid-liquid interface of bcc elements[J]. Physical Review A, 1987, 35 (6): 2611- 2618.
DOI |
| 32 |
TÓTH G I , PROVATAS N . Erratum: Advanced Ginzburg-Landau theory of freezing: A density-functional approach[J]. Physical Review B, 2014, 90 (17): 179901.
DOI |
| 33 |
TÓTH G I , PROVATAS N . Advanced Ginzburg-Landau theory of freezing: A density-functional approach[J]. Physical Review B, 2014, 90 (10): 104101.
DOI |
| 34 |
MAJANIEMI S , PROVATAS N . Deriving surface-energy anisotropy for phenomenological phase-field models of solidification[J]. Physical Review E, 2009, 79 (1): 011607.
DOI |
| 35 |
WU Kuoan , WANG Chinghao , HOYT J J , et al. Ginzburg-Landau theory of the bcc-liquid interface kinetic coefficient[J]. Physical Review B, 2015, 91 (1): 014107.
DOI |
| 36 |
WU Kuoan , VOORHEES P W . Phase field crystal simulations of nanocrystalline grain growth in two dimensions[J]. Acta Materialia, 2012, 60 (1): 407- 419.
DOI |
| 37 |
UPMANYU M , SROLOVITZ D J , LOBKOVSKY A E , et al. Simultaneous grain boundary migration and grain rotation[J]. Acta Materialia, 2006, 54 (7): 1707- 1719.
DOI |
| [1] | Wenjing MA, Jin WANG, Hui GUO, Meini LYU, Hongze ZHANG, Dongde LI. Phase Field Crystal Method Study on Inhibitory Mechanism of the Growth of Kirkendall Voids During Deformation Process at the Interface of Metal Micro Interconnect Structures [J]. Chinese Journal of Computational Physics, 2023, 40(4): 416-424. |
| [2] | Hongming LI, Maosheng LI. Effect of Irradiation on Mechanical Properties of Polycrystalline Copper: Crystal Plasticity Finite Element Method [J]. Chinese Journal of Computational Physics, 2022, 39(1): 6-16. |
| [3] | Huaimin GUO, Guozhong ZHAO, Lijuan JIANG. Screw Dislocation Interacting with Lip-shaped Crack in Magnetoelectroelastic Media [J]. Chinese Journal of Computational Physics, 2022, 39(1): 33-40. |
| [4] | GUO Huaimin, ZHAO Guozhong. Multiple Screw Parallel Dislocations and a Griffith Crack in Magnetoelectroelastic Body [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(2): 198-204. |
| [5] | GAO Yingjun, YANG Ruilin, HUANG Lilin, LIU Yao. Phase Field Crystal Simulation in Nano-scale for Crack Extension with Pre-deformation [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2017, 34(4): 453-460. |
| [6] | LUO Zhirong, GAO Yingjun, MAO Hong, LU Chengjian, HUANG Shiye. Phase Field Modeling of Columnar Grain Growth:Effect of Second-Phase Particles [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2016, 33(3): 367-373. |
| [7] | GAO Yingjun, WANG Jiangfan, LUO Zhirong, LU Qianghua, LIU Yao. Nano-twin Structure Simulation with Phase Field Crystal Method [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2013, 30(4): 577-581. |
| [8] | PANG Weiwei, ZHANG Guangcai, XU Aiguo, LU Guo. Size Effect in Void Growth and Coalescence of Face-centered Cubic Copper Crystals [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2011, 28(4): 540-546. |
| [9] | LU Guo, FANG Buqing, ZHANG Guangcai. Constructing Dislocation Atom Distribution withContinuous Dislocation Theory [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2010, 27(2): 195-202. |
| [10] | WANG Chaoying, MENG Qingyuan, LI Chengxiang, ZHONG Kangyou, YANG Zhifu. Molecular Simulation on Migration of Kinks on a 30° Partial Dislocation in Silicon [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2008, 25(4): 488-492. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © Chinese Journal of Computational Physics
E-mail: jswl@iapcm.ac.cn
Supported by Beijing Magtech Co., Ltd.
