Chinese Journal of Computational Physics ›› 2022, Vol. 39 ›› Issue (6): 651-665.DOI: 10.19596/j.cnki.1001-246x.8505
• Research Reports • Previous Articles Next Articles
Hongfei ZHAN1, Zhenning CAI2, Guanghui HU1,3,4,*( )
)
Received:2022-01-11
Online:2022-11-25
Published:2023-04-01
Contact:
Guanghui HU
Hongfei ZHAN, Zhenning CAI, Guanghui HU. Wigner Ground State Calculation Based on Imaginary Time Propagation Method and Spectral Method[J]. Chinese Journal of Computational Physics, 2022, 39(6): 651-665.
Add to citation manager EndNote|Ris|BibTeX
URL: http://www.cjcp.org.cn/EN/10.19596/j.cnki.1001-246x.8505
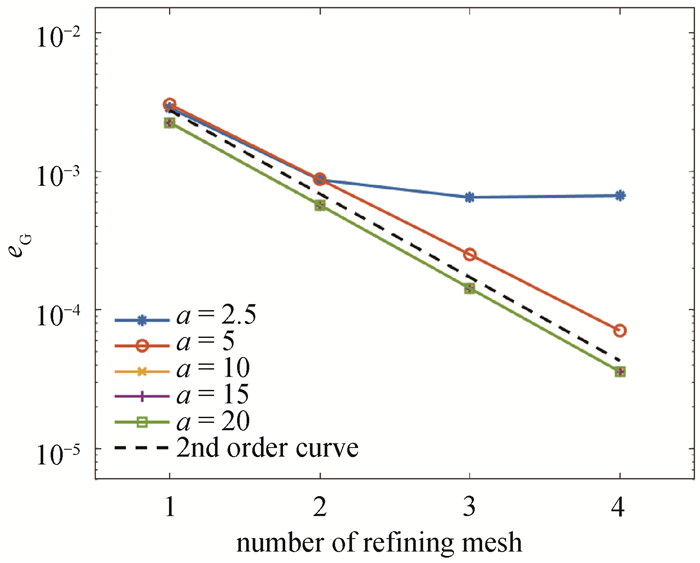
Fig.1 Errors $ e_{\mathrm{G}}=\max _{|\alpha| \leqslant M}\left\|f_\alpha-f_\alpha^{\text {exc }}\right\|_{\infty}$ for 2-D harmonic oscillator at M=18
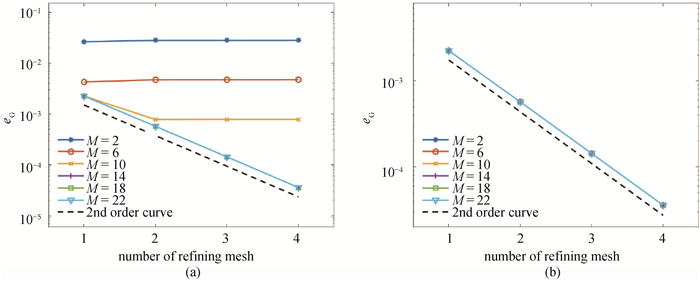
Fig.2 Errors with simplified Grad moment method for 2-D harmonic oscillator (a) total errors $e_{\mathrm{G}}=\max _{|\alpha| \leqslant M}\left\|f_\alpha-f_\alpha^{\text {exc }}\right\|_\infty $; (b) density errors $ e_\rho=\left\|\rho-\rho^{\mathrm{exc}}\right\|_{\infty}$
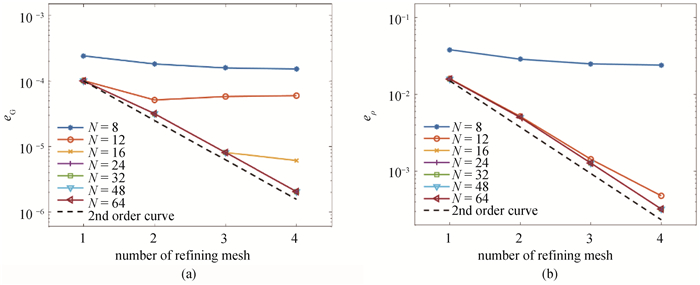
Fig.3 Errors with Fourier pseudo-spectral method for 2-D harmonic oscillator (a) total errors $ e_{\mathrm{F}}=\max _{\alpha \in I_N}\left\|a_\alpha-a_\alpha^{\text {exc }}\right\|_{\infty}$; (b) density errors $e_\rho=\left\|\rho-\rho^\text {exc }\right\|_{\infty} $
| h | Wigner: 简化Grad矩方法 | Schrödinger | ||||||||
| M = 0 | M = 2 | M = 4 | ||||||||
| error | energy | error | energy | error | energy | energy | ||||
| 2.00 × 10-1 | 2.106 8 × 10-3 | 1.317 18 | 1.971 0 × 10-3 | 1.317 27 | 2.287 9 × 10-3 | 1.315 68 | 1.314 76 | |||
| 1.00 × 10-1 | 5.821 7 × 10-4 | 1.313 98 | 5.147 9 × 10-4 | 1.314 03 | 6.033 8 × 10-4 | 1.313 60 | 1.313 47 | |||
| 5.00 × 10-2 | 1.706 3 × 10-4 | 1.313 23 | 1.368 0 × 10-4 | 1.313 26 | 1.597 9 × 10-4 | 1.313 15 | 1.313 15 | |||
| 2.50 × 10-2 | 5.380 8 × 10-5 | 1.313 06 | 3.682 7 × 10-5 | 1.313 08 | 4.265 6 × 10-5 | 1.313 05 | 1.313 07 | |||
| 1.25 × 10-2 | 1.772 3 × 10-5 | 1.313 04 | 9.211 2 × 10-6 | 1.313 04 | 1.067 7 × 10-5 | 1.313 04 | 1.313 05 | |||
| 6.25 × 10-3 | 5.268 8 × 10-6 | 1.313 03 | 3.002 1 × 10-6 | 1.313 04 | 3.446 0 × 10-6 | 1.313 04 | 1.313 04 | |||
Table 1 Density errors ‖ρwGrad - ρsfinest‖∞ and energies of contact-interacting Hooke atom with simplified Grad moment method
| h | Wigner: 简化Grad矩方法 | Schrödinger | ||||||||
| M = 0 | M = 2 | M = 4 | ||||||||
| error | energy | error | energy | error | energy | energy | ||||
| 2.00 × 10-1 | 2.106 8 × 10-3 | 1.317 18 | 1.971 0 × 10-3 | 1.317 27 | 2.287 9 × 10-3 | 1.315 68 | 1.314 76 | |||
| 1.00 × 10-1 | 5.821 7 × 10-4 | 1.313 98 | 5.147 9 × 10-4 | 1.314 03 | 6.033 8 × 10-4 | 1.313 60 | 1.313 47 | |||
| 5.00 × 10-2 | 1.706 3 × 10-4 | 1.313 23 | 1.368 0 × 10-4 | 1.313 26 | 1.597 9 × 10-4 | 1.313 15 | 1.313 15 | |||
| 2.50 × 10-2 | 5.380 8 × 10-5 | 1.313 06 | 3.682 7 × 10-5 | 1.313 08 | 4.265 6 × 10-5 | 1.313 05 | 1.313 07 | |||
| 1.25 × 10-2 | 1.772 3 × 10-5 | 1.313 04 | 9.211 2 × 10-6 | 1.313 04 | 1.067 7 × 10-5 | 1.313 04 | 1.313 05 | |||
| 6.25 × 10-3 | 5.268 8 × 10-6 | 1.313 03 | 3.002 1 × 10-6 | 1.313 04 | 3.446 0 × 10-6 | 1.313 04 | 1.313 04 | |||
| h | Wigner: 傅里叶伪谱方法 | Schrödinger | ||||||||
| N = 16 | N = 32 | N = 64 | ||||||||
| error | energy | error | energy | error | energy | energy | ||||
| 2.00 × 10-1 | 4.518 0 × 10-4 | 1.212 67 | 2.218 5 × 10-3 | 1.317 50 | 2.218 9 × 10-3 | 1.317 52 | 1.314 76 | |||
| 1.00 × 10-1 | 2.237 4 × 10-3 | 1.209 54 | 5.3788 × 10-4 | 1.314 20 | 5.382 8 × 10-4 | 1.314 22 | 1.313 47 | |||
| 5.00 × 10-2 | 2.667 7 × 10-3 | 1.208 75 | 1.3675 × 10-4 | 1.313 32 | 1.371 5 × 10-4 | 1.313 34 | 1.313 15 | |||
| 2.50 × 10-2 | 2.775 3 × 10-3 | 1.208 56 | 3.6469 × 10-5 | 1.313 10 | 3.646 9 × 10-5 | 1.313 12 | 1.313 07 | |||
| 1.25 × 10-2 | 2.802 2 × 10-3 | 1.208 51 | 1.1414 × 10-5 | 1.313 04 | 1.181 5 × 10-5 | 1.313 06 | 1.313 05 | |||
| 6.25 × 10-3 | 2.808 9 × 10-3 | 1.208 45 | 5.1510 × 10-6 | 1.313 03 | 5.552 2 × 10-6 | 1.313 05 | 1.313 04 | |||
Table 2 Density errors ‖ρwFourier - ρsfinest‖∞ and energies of contact-interacting Hooke atom with Fourier pseudo-spectral method
| h | Wigner: 傅里叶伪谱方法 | Schrödinger | ||||||||
| N = 16 | N = 32 | N = 64 | ||||||||
| error | energy | error | energy | error | energy | energy | ||||
| 2.00 × 10-1 | 4.518 0 × 10-4 | 1.212 67 | 2.218 5 × 10-3 | 1.317 50 | 2.218 9 × 10-3 | 1.317 52 | 1.314 76 | |||
| 1.00 × 10-1 | 2.237 4 × 10-3 | 1.209 54 | 5.3788 × 10-4 | 1.314 20 | 5.382 8 × 10-4 | 1.314 22 | 1.313 47 | |||
| 5.00 × 10-2 | 2.667 7 × 10-3 | 1.208 75 | 1.3675 × 10-4 | 1.313 32 | 1.371 5 × 10-4 | 1.313 34 | 1.313 15 | |||
| 2.50 × 10-2 | 2.775 3 × 10-3 | 1.208 56 | 3.6469 × 10-5 | 1.313 10 | 3.646 9 × 10-5 | 1.313 12 | 1.313 07 | |||
| 1.25 × 10-2 | 2.802 2 × 10-3 | 1.208 51 | 1.1414 × 10-5 | 1.313 04 | 1.181 5 × 10-5 | 1.313 06 | 1.313 05 | |||
| 6.25 × 10-3 | 2.808 9 × 10-3 | 1.208 45 | 5.1510 × 10-6 | 1.313 03 | 5.552 2 × 10-6 | 1.313 05 | 1.313 04 | |||
| h | K = 0 | K = 1 | K = 2 | |||||
| error | rate | error | rate | error | rate | |||
| 2.00 × 10-1 | 2.101 5 × 10-3 | 1.970 0 × 10-3 | 2.286 6 × 10-3 | |||||
| 1.00 × 10-1 | 5.769 0 × 10-4 | 1.865 0 | 5.137 8 × 10-4 | 1.939 0 | 6.020 1 × 10-4 | 1.925 3 | ||
| 5.00 × 10-2 | 1.653 6 × 10-4 | 1.802 7 | 1.358 0 × 10-4 | 1.919 7 | 1.584 1 × 10-4 | 1.926 1 | ||
| 2.50 × 10-2 | 4.854 0 × 10-5 | 1.768 4 | 3.582 0 × 10-5 | 1.922 6 | 4.128 2 × 10-5 | 1.940 1 | ||
| 6.25 × 10-3 | 1.245 4 × 10-5 | 1.962 5 | 8.204 2 × 10-6 | 2.126 3 | 9.303 2 × 10-6 | 2.149 7 | ||
Table 3 Relative errors $\operatorname{max}_{0 \leqslant k \leqslant K}\left\|f_{2 k}-f_{2 k}^{\text {finest }}\right\|_{\infty} $ and convergence order with simplified Grad moment method for contact-interacting Hooke atom
| h | K = 0 | K = 1 | K = 2 | |||||
| error | rate | error | rate | error | rate | |||
| 2.00 × 10-1 | 2.101 5 × 10-3 | 1.970 0 × 10-3 | 2.286 6 × 10-3 | |||||
| 1.00 × 10-1 | 5.769 0 × 10-4 | 1.865 0 | 5.137 8 × 10-4 | 1.939 0 | 6.020 1 × 10-4 | 1.925 3 | ||
| 5.00 × 10-2 | 1.653 6 × 10-4 | 1.802 7 | 1.358 0 × 10-4 | 1.919 7 | 1.584 1 × 10-4 | 1.926 1 | ||
| 2.50 × 10-2 | 4.854 0 × 10-5 | 1.768 4 | 3.582 0 × 10-5 | 1.922 6 | 4.128 2 × 10-5 | 1.940 1 | ||
| 6.25 × 10-3 | 1.245 4 × 10-5 | 1.962 5 | 8.204 2 × 10-6 | 2.126 3 | 9.303 2 × 10-6 | 2.149 7 | ||
| h | N = 16 | N = 32 | N = 64 | |||||
| error | rate | error | rate | error | rate | |||
| 2.00 × 10-1 | 2.357 1 × 10-3 | 2.213 4 × 10-3 | 2.213 3 × 10-3 | |||||
| 1.00 × 10-1 | 5.715 5 × 10-4 | 2.044 1 | 5.327 3 × 10-4 | 2.054 8 | 5.327 2 × 10-4 | 2.054 8 | ||
| 5.00 × 10-2 | 1.412 7 × 10-4 | 2.016 5 | 1.316 0 × 10-4 | 2.017 3 | 1.316 0 × 10-4 | 2.017 3 | ||
| 2.50 × 10-2 | 3.362 4 × 10-5 | 2.070 8 | 3.131 8 × 10-5 | 2.071 1 | 3.131 8 × 10-5 | 2.071 1 | ||
| 6.25 × 10-3 | 6.726 6 × 10-6 | 2.321 6 | 6.263 3 × 10-6 | 2.322 0 | 6.263 2 × 10-6 | 2.322 0 | ||
Table 4 Relative errors $\max _{\alpha \in \mathcal{I}_N}\left\|a_\alpha-a_\alpha^{\text {finest }}\right\|_{\infty} $ and convergence order with Fourier pseudo-spectral method for contact-interacting Hooke atom
| h | N = 16 | N = 32 | N = 64 | |||||
| error | rate | error | rate | error | rate | |||
| 2.00 × 10-1 | 2.357 1 × 10-3 | 2.213 4 × 10-3 | 2.213 3 × 10-3 | |||||
| 1.00 × 10-1 | 5.715 5 × 10-4 | 2.044 1 | 5.327 3 × 10-4 | 2.054 8 | 5.327 2 × 10-4 | 2.054 8 | ||
| 5.00 × 10-2 | 1.412 7 × 10-4 | 2.016 5 | 1.316 0 × 10-4 | 2.017 3 | 1.316 0 × 10-4 | 2.017 3 | ||
| 2.50 × 10-2 | 3.362 4 × 10-5 | 2.070 8 | 3.131 8 × 10-5 | 2.071 1 | 3.131 8 × 10-5 | 2.071 1 | ||
| 6.25 × 10-3 | 6.726 6 × 10-6 | 2.321 6 | 6.263 3 × 10-6 | 2.322 0 | 6.263 2 × 10-6 | 2.322 0 | ||
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
DOI |
| 6 |
DOI |
| 7 |
DOI |
| 8 |
DOI |
| 9 |
DOI |
| 10 |
DOI |
| 11 |
DOI |
| 12 |
DOI |
| 13 |
DOI |
| 14 |
DOI |
| 15 |
|
| 16 |
DOI |
| 17 |
DOI |
| 18 |
DOI |
| 19 |
DOI |
| 20 |
戴小英. 电子结构计算的数值方法与理论[J]. 计算数学, 2020, 42 (2): 131- 158.
|
| 21 |
DOI |
| 22 |
DOI |
| 23 |
DOI |
| 24 |
DOI |
| 25 |
DOI |
| 26 |
DOI |
| 27 |
|
| 28 |
DOI |
| 29 |
DOI |
| 30 |
DOI |
| 31 |
DOI |
| 32 |
DOI |
| 33 |
DOI |
| 34 |
DOI |
| 35 |
DOI |
| 36 |
|
| 37 |
|
| 38 |
DOI |
| 39 |
DOI |
| 40 |
DOI |
| 41 |
DOI |
| 42 |
DOI |
| 43 |
DOI |
| 44 |
|
| 45 |
DOI |
| 46 |
DOI |
| 47 |
DOI |
| 48 |
DOI |
| 49 |
DOI |
| 50 |
|
| 51 |
DOI |
| 52 |
DOI |
| 53 |
FIOLHAIS C, NOGUEIRA F, MARQUES M. A Primer in density functional theory[M]. [S. l.]: Springer, 2003.
|
| 54 |
DOI |
| [1] | Liyuan WU, Suying ZHANG. Ground State of Bose-Einstein Condensates in a Spin-dependent Optical Lattice [J]. Chinese Journal of Computational Physics, 2022, 39(5): 617-623. |
| [2] | Wumaierjiang NAIPISAI, Haokui YAN, Abulimiti BUMALIYA, Danqi WANG, Mei XIANG, Huan AN. Spectrum and Dissociation Characteristics of CHBr3 Molecule Under External Electric Fields [J]. Chinese Journal of Computational Physics, 2022, 39(5): 624-630. |
| [3] | Hang JI, Zhongmou SUN, Zhuoyan ZHOU, Yuzhu LIU. Modulation and Degradation of CO Molecular and Ionic Properties with External Electric Field [J]. Chinese Journal of Computational Physics, 2022, 39(3): 327-334. |
| [4] | Hui GAO, Zaifa YANG, Jingfen ZHAO, Huimin YUAN, Zhie LIU, Xian ZHAO. Effect of Nb, Sn, Cu, Fe and Cr on Zr (0001) Surface Nodular Corrosion Resistance: First Principles Study [J]. Chinese Journal of Computational Physics, 2022, 39(1): 101-108. |
| [5] | WU Ming, ZHOU Ruirui, LI Benwen. Collocation Spectral Method for Radiative Heat Transfer in One-dimensional Cylindrical Medium with Graded Index [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(3): 320-326. |
| [6] | CHAI Rukuan, LIU Yuetian, YANG Li, ZHANG Yixin, XIN Jing, MA Jing. Adsorption Mechanism of Two Organic Molecules with Different Polarities on Calcite (104) Surface: Density Functional Theory Study [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(2): 221-230. |
| [7] | CHEN Yu, XING Yongming. Effect of Hydrostatic Pressure on Magneto-optical Properties of Al14Mn2P16: A Density Functional Theory Study [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(2): 231-239. |
| [8] | YIN Haifeng, ZENG Chunhua, CHEN Wenjing. Plasmon Excitations in Two-dimensional Binary Silicon Carbide Nanostructures [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(5): 603-609. |
| [9] | HE Zhiwei, ZHANG Xiurong. Structure and Properties of (BN)25 Clusters [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(2): 219-224. |
| [10] | ZHOU Kang, FENG Qing, TIAN Yun, LI Ke, ZHOU Qingbin. Oxidizing Gas NO2 Optical Gas Sensing Characteristics of Transition Metal Cu and Cr Doped TiO2 Surfaces [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(6): 702-710. |
| [11] | XIE Jianming, CHEN Hongxia, ZHUANG Guoce. A study on Physical Properties of Mn-Doped (ZnSe)12 Clusters [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(4): 481-486. |
| [12] | LI Dawei, GAO Yunliang, ZHU Yuanjiang, LI Jinping. Density Functional Theory Calculations of Ga Doped δ-Pu [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(4): 487-493. |
| [13] | LIN Yan, LIU Yun, PENG Qingwei, WEI Xiaonan, TANG Yanlin. Calculation of Structural Parameters and Frontier Orbital of Cucurbituril (5-10) with Density Functional Theory [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(2): 221-229. |
| [14] | CHEN Hongxia, DU Sijie, ZHUANG Guoce. Structure and magnetic properties of Ni-doped ZnO clusters [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(1): 112-118. |
| [15] | LI Anjun, ZHU Yuanqiang, SU Hong, YANG Zehong. Mechanism of Acetylenic-Keton Intramolecular Cyclization Reaction Catalyzed by AuCl3 [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2017, 34(6): 679-684. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © Chinese Journal of Computational Physics
E-mail: jswl@iapcm.ac.cn
Supported by Beijing Magtech Co., Ltd.
