润湿梯度作用下液滴在倾斜表面向上运动的格子Boltzmann模拟

doi:10.19596/j.cnki.1001-246x.8325

摘要/Abstract

摘要：

采用基于Shan-Chen伪势模型的格子Boltzmann方法，对液滴在存在润湿梯度的倾斜表面上克服重力、自下而上运动的过程进行模拟。探究润湿梯度、液滴尺寸、Bond数以及表面倾斜角度对液滴运动的影响。计算结果表明：液滴在运动过程中，内部会出现沿斜面向上的速度矢量，润湿梯度越大，液滴运动速度越快，润湿长度也越长，且动态接触角减小速率越快。液滴尺寸和Bond数对液滴运动的影响较小，但存在临界Bond数，超过该临界Bond数时，液滴将沿梯度润湿表面向下运动。表面倾角对液滴运动有显著影响，倾角增大，液滴运动速度和润湿长度都明显减小。

关键词: 格子Boltzmann方法, 润湿梯度, 液滴, Bond数, 倾斜角度

Abstract:

A lattice Boltzmann method based on Shan-Chen pseudo-potential model was used to simulate the process of a droplet overcoming gravity and moving upward on a inclined plane with wetting gradient. Effects of wetting gradient, droplet size, Bond number and surface inclination angle on droplet motion were investigated. It shows that velocity vector appears in the droplet moving upwards along the slope. The greater the wetting gradient is, the faster the droplet moves, and the longer the wetting length is, and the faster the dynamic contact angle decreases. Droplet size and Bond number have weak influence on droplet motion, but there is a critical Bond number, beyond which the droplet moves down along the gradient wetting surface. The surface inclination angle has a significant effect on the droplet motion. As the inclination angle increases, the droplet motion speed and wetting length are significantly reduced.

Key words: lattice Boltzmann method, wetting gradient, droplet, Bond number, inclination angle

中图分类号:

O359

陈露, 高明, 梁佳, 王东民, 赵玉刚, 章立新. 润湿梯度作用下液滴在倾斜表面向上运动的格子Boltzmann模拟[J]. 计算物理, 2021, 38(6): 672-682.

Lu CHEN, Ming GAO, Jia LIANG, Dongmin WANG, Yugang ZHAO, Lixin ZHANG. Droplet Upward Movement on an Inclined Surface Under Wetting Gradient: Lattice Boltzmann Simulation[J]. Chinese Journal of Computational Physics, 2021, 38(6): 672-682.

图/表 14

图1 物理模型

Fig.1 Physical model

图2 D2Q9模型

Fig.2 D2Q9 model

图3 Young-Laplace定律验证

Fig.3 Verification of Young-Laplace law

图4 相互作用强度与接触角的关系

Fig.4 Relation between interaction strength and contact angle

图5 液滴在水平润湿梯度运动示意图

Fig.5 Schematic of a droplet in a horizontal wetting gradient movement

图6 模拟结果与理论预测值的对比

Fig.6 Comparison of simulation result and theoretical prediction

图7 液滴在不同倾斜润湿梯度表面向上运动的形态变化

Fig.7 Morphological change of a droplet moving upward on a surface with different inclined wetting gradients

图8 不同润湿梯度下液滴运动的速度场

Fig.8 Velocity field of droplet movement under different wetting gradients

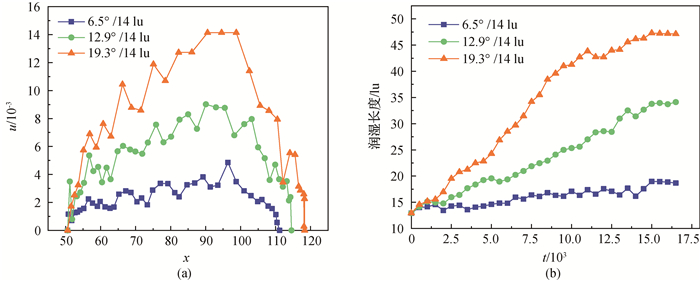
图9 不同润湿梯度下(a)液滴运动速度随位置的变化和(b)润湿长度随时间的变化

Fig.9 (a) Variation of droplet velocity with position and (b) variation of wetting length with time under different wetting gradients

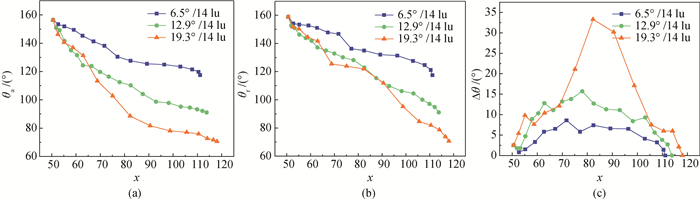
图10 (a) 动态前进接触角和(b)后退接触角以及(c)两者的差值随位置的变化

Fig.10 Variation of (a) dynamic advancing contact angle and (b) receding contact angle and (c) their difference with position

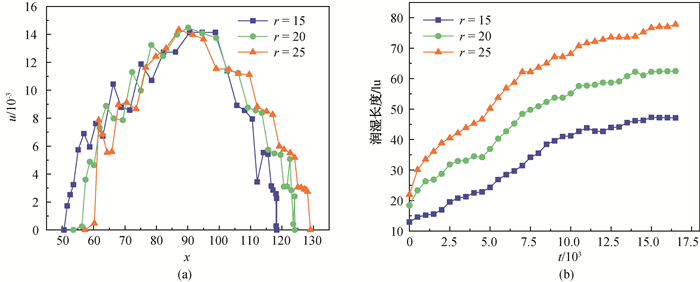
图11 不同尺寸液滴(a)运动速度随位置的变化和(b)润湿长度随时间的变化

Fig.11 (a) Velocity of droplet with different size changes with position and (b) wetting length changes with time

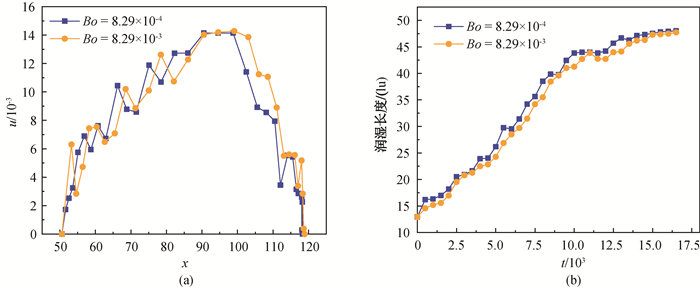
图12 不同Bond数下(a)液滴运动速度随位置的变化和(b)润湿长度随时间的变化(r=15，19.3°/14 lu)

Fig.12 (a) Variation of droplet velocity with position and (b) variation of wetting length with time at different Bond numbers (r=15, 19.3°/14 lu)

图13 临界Bond数与润湿梯度的关系

Fig.13 Relation between critical Bond number and wetting gradient

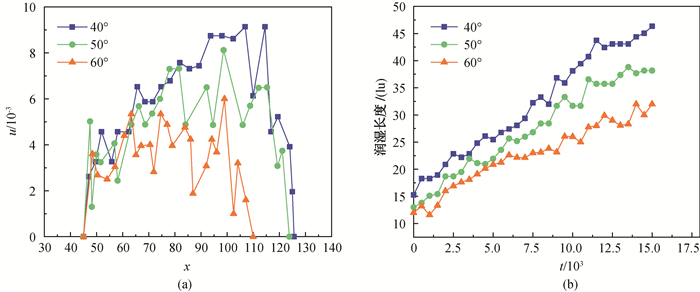
图14 在不同倾斜角度下液滴(a)运动速度随位置的变化和(b)润湿长度随时间的变化

Fig.14 (a) Variation of droplet velocity with position and (b) variation of wetting length with time at different tilt angles

参考文献 31

1	CHEN H, ZHANG P, ZHANG L, et al. Continuous directional water transport on the peristome surface of Nepenthes alata[J]. Nature: International Weekly Journal of Science, 2016, 532 (7597): 85- 100.
2	宋云云. 仿生结构化石墨烯多功能表面的制备及集水性能研究[D]. 长春: 吉林大学, 2019.
3	ZHU X, WANG H, LIAO Q, et al. Experiments and analysis on self-motion behaviors of liquid droplets on gradient surfaces[J]. Experimental Thermal and Fluid Science, 2009, 33 (6): 947- 954. DOI
4	PARADISANOS I, FOTAKIS C, ANASTASIADIS S H, et al. Gradient induced liquid motion on laser structured black Si surfaces[J]. Applied Physics Letters, 2015, 107 (11): 1403- 1531.
5	LIU C, SUN J, LI J, et al. Long-range spontaneous droplet self-propulsion on wettability gradient surfaces[J]. Scientific Reports, 2017, 7 (1): 7552. DOI
6	DENG S, SHANG W, FENG S, et al. Controlled droplet transport to target on a high adhesion surface with multi-gradients[J]. Scientific Reports, 2017, 7 (1): 1- 8. DOI
7	CHOWDHURY I U, SINHA MAHAPATRA P, SEN A K. Self driven droplet transport: Effect of wettability gradient and confinement[J]. Physics of Fluids, 2019, 31 (4): 1- 12.
8	MOHAMAD A A. Lattice Boltzmann method: Fundamentals and engineering applications with computer codes[M]. ERT Press, 2011.
9	何雅玲, 王勇, 李庆. 格子Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2009.
10	HU Y, SUN T. Three-dimensional numerical simulation of dynamics characteristics of two rising bubbles with lattice Boltzmann method[J]. Chinese Journal of Computational Physics, 2020, 37 (3): 277- 283.
11	LOU Q, ZANG C, WANG H, et al. Interfacial dynamics of immiscible gas-liquid two-phase flow for CO₂ in microchannel: Lattice Boltzmann method[J]. Chinese Journal of Computational Physics, 2019, 36 (2): 153- 164.
12	LV Y, NIE D, LIN J. Lattice Boltzmann simulation of gas bubble merging in three dimensions[J]. Chinese Journal of Computational Physics, 2015, 32 (5): 553- 560.
13	ZHANG R, DI Q, WANG X, et al. Lattice Boltzmann simulation of flow in a micro-channel[J]. Chinese Journal of Computational Physics, 2011, 28 (2): 225- 229.
14	GUNSTENSEN A K, ROTHMAN D H, ZALESKI S, et al. Lattice Boltzmann model of immiscible fluids[J]. Physical Review A, 1991, 43 (8): 4320- 4327. DOI
15	SHAN X, CHEN H. Lattice Boltzmann model for simulating flows with multiple phases and components[J]. Phys Rev E, 1993, 47 (3): 1815- 1819. DOI
16	SWIFT M R, ORLANDINI E, OSBORN W R, et al. Lattice Boltzmann simulations of liquid-gas and binary fluid systems[J]. Physical Review E, 1996, 54 (5): 5041. DOI
17	SWIFT M R, OSBORN W R, YEOMANS J M. Lattice Boltzmann simulation of non-ideal fluids[J]. Physical Review Letters, 1995, 75 (5): 830- 833. DOI
18	HE X, SHAN X, DOOLEN G D. Discrete Boltzmann equation model for nonideal gases[J]. Physical Review E, 1998, 57 (1): R13- R16. DOI
19	HE X, CHEN S, ZHANG R. A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability[J]. Journal of Computational Physics, 1999, 152 (2): 642- 663. DOI
20	郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2009.
21	石自媛, 胡国辉, 周哲玮. 润湿性梯度驱动液滴运动的格子Boltzmann模拟[J]. 物理学报, 2010, 59 (4): 2595- 2600.
22	HUANG J J, SHU C, CHEW Y T. Numerical investigation of transporting droplets by spatiotemporally controlling substrate wettability[J]. Journal of Colloid and Interface Science, 2008, 328 (1): 124- 133. DOI
23	DENG Z, ZHANG C, SHEN C, et al. Self-propelled dropwise condensation on a gradient surface[J]. International Journal of Heat and Mass Transfer, 2017, 114, 419- 429. DOI
24	王鑫, 陈振乾. 梯度润湿表面上液滴定向迁移及合并行为的格子Boltzmann模拟[J]. 计算力学学报, 2019, 36 (4): 511- 519.
25	许术方, 李培生, 马明, 等. 非均匀润湿性表面捕获液滴的数值模拟[J]. 南昌大学学报(工科版), 2019, 41 (2): 183- 188. DOI
26	QIAN Y H, D'HUMIÈRES D, LALLEMAND P. Lattice BGK models for Navier-Stokes equations[J]. Europhysics Letters, 1992, 17 (6): 479- 484. DOI
27	SUKOP M C, Jr D T T . Lattice Boltzmann modeling: An introduction for geoscientists and engineers[M]. Springer Publishing Company, 2006.
28	RAPHAËL E. Spreading of droplets on a patchy surface[J]. C R Acad Sci Paris, 1988, 306 (2): 751- 754.
29	GONG S, CHENG P. Numerical investigation of droplet motion and coalescence by an improved lattice Boltzmann model for phase transitions and multiphase flows[J]. Computers & Fluids, 2012, 53 (none): 93- 104.
30	廖强, 王宏, 朱恂, 等. 梯度表面能材料上液滴运动特性实验[J]. 工程热物理学报, 2007, 28 (1): 134- 136. DOI
31	王宏, 廖强, 朱恂. 梯度表面能材料上液滴运动机理[J]. 化工学报, 2007, 58 (9): 2313- 2320. DOI

[1]	冯舒婷, 戴厚平, 宋通政. 二维空间分数阶反应扩散方程组的格子Boltzmann方法[J]. 计算物理, 2022, 39(6): 666-676.
[2]	刘嘉鑫, 郑林, 张贝豪. 多孔介质方腔内双扩散自然对流熵产的格子Boltzmann模拟[J]. 计算物理, 2022, 39(5): 549-563.
[3]	林品亮, 冯欢欢, 董宇红. 具有多孔介质覆面层的柱体绕流流场分析[J]. 计算物理, 2022, 39(4): 418-426.
[4]	张巧玲, 景何仿. 三维曲面腔顶盖驱动流的MRT-LBM研究[J]. 计算物理, 2022, 39(4): 427-439.
[5]	魏雪丹, 戴厚平, 李梦军, 郑洲顺. 一维空间Riesz分数阶对流扩散方程的格子Boltzmann方法[J]. 计算物理, 2021, 38(6): 683-692.
[6]	娄钦, 汤升, 王浩原. 基于格子Boltzmann大密度比模型的多孔介质内气泡动力学行为数值模拟[J]. 计算物理, 2021, 38(3): 289-300.
[7]	梁佳, 高明, 陈露, 王东民, 章立新. 液滴撞击不同湿润性固壁面上静止液滴的格子Boltzmann研究[J]. 计算物理, 2021, 38(3): 313-323.
[8]	袁俊杰, 叶欣, 单彦广. 格子Boltzmann方法模拟填充纳米流体三角形腔内的自然对流[J]. 计算物理, 2021, 38(1): 57-68.
[9]	王坚毅, 潘振海, 吴慧英. 微通道内椭球颗粒惯性聚焦行为数值研究[J]. 计算物理, 2020, 37(6): 677-686.
[10]	高辉, 高瑞峰, 姚孟君, 张道旭, 彭澄宇, 张莹. 液滴撞击液膜的流热耦合界面追踪方法数值模拟[J]. 计算物理, 2020, 37(4): 422-430.
[11]	唐古月, 娄钦, 李凌. 格子Boltzmann方法分析加热尺寸和瑞利数对可变形开口腔内自然对流的影响[J]. 计算物理, 2020, 37(3): 263-276.
[12]	胡玉, 孙涛. 三维格子Boltzmann方法研究上升双气泡的运动特性[J]. 计算物理, 2020, 37(3): 277-283.
[13]	连小龙, 陈岳, 李培生, 张莹, 李伟, 刘强. 基于MRT-LB伪势模型的液滴撞击液膜数值研究[J]. 计算物理, 2020, 37(1): 79-87.
[14]	居隆, 张春华, 陈松泽, 郭照立. 多孔介质中非等温互溶流体驱替过程的格子Boltzmann研究[J]. 计算物理, 2019, 36(6): 648-658.
[15]	孙涛, 刘志斌, 范伟, 秦海杰. 过热液体中蒸汽泡上升过程的格子Boltzmann三维数值模拟[J]. 计算物理, 2019, 36(6): 659-664.