多孔介质方腔内双扩散自然对流熵产的格子Boltzmann模拟

doi:10.19596/j.cnki.1001-246x.8484

摘要/Abstract

摘要：

用格子Boltzmann方法对倾斜多孔介质方腔内流体双扩散自然对流的熵产进行数值模拟, 分析孔隙率(0.2≤ε≤0.9)、瑞利数(10³≤Ra≤10⁶)、浮力比(-4≤Br≤2)和倾斜角(0°≤γ≤80°)对局部熵产与总熵产的影响。结果表明: ①当ε和Ra增加时, 因流动与传热传质引起的局部熵产峰值升高, 流动熵产对总熵产的贡献逐步增大, 净流体摩擦项在流动熵产中占比升高; ②Br=-1是局部熵产分布发生变化的临界值, 此时熵产趋于零; ③随着倾斜角的增大, 局部流动熵产的高熵产区域沿着顺时针方向移动; 当γ=40°时, 净流体摩擦造成的熵产达到极大值而达西耗散造成的熵产峰值出现在γ=60°。

关键词: 双扩散自然对流, 熵产, 多孔介质, 格子Boltzmann方法

Abstract:

A Darcy-Brinkman-Forchheimer model based lattice Boltzmann method is conducted to the simnlation of double-diffusive natural convection in an inclined square porous enclosure. Effects of porosity (0.2≤ε≤0.9), Rayleigh number (10³≤Ra≤10⁶), buoyancy ratio (-4≤Br≤2) and inclination angle (0°≤γ≤80°) on the local and total entropy generation are systematically investigated. It shows that as ε and Ra increased, peaks of local entropy generation due to heat transfer, fluid friction and mass transfer grow higher and the contribution of fluid friction to total entropy generation increased prominently. In addition, the clear fluid term has more influence on fluid friction entropy generation. Br=-1 is a critical value for the change of local entropy generation distribution. At the same time, the total entropy generation tends to zero. With the increase of inclination angle, the high entropy generation region of local fluid friction entropy generation moves clockwise. The maximum entropy caused by clear fluid term and Darcy dissipation term appears at 40° and 60°, respectively.

Key words: double-diffusive natural convection, entropy generation, porous media, lattice Boltzmann method

刘嘉鑫, 郑林, 张贝豪. 多孔介质方腔内双扩散自然对流熵产的格子Boltzmann模拟[J]. 计算物理, 2022, 39(5): 549-563.

Jiaxin LIU, Lin ZHENG, Beihao ZHANG. Entropy Generation in Double-diffusive Natural Convection in a Square Porous Enclosure: Lattice Boltzmann Method[J]. Chinese Journal of Computational Physics, 2022, 39(5): 549-563.

图/表 12

图1 物理模型示意图

Fig.1 A schematic of the physical model

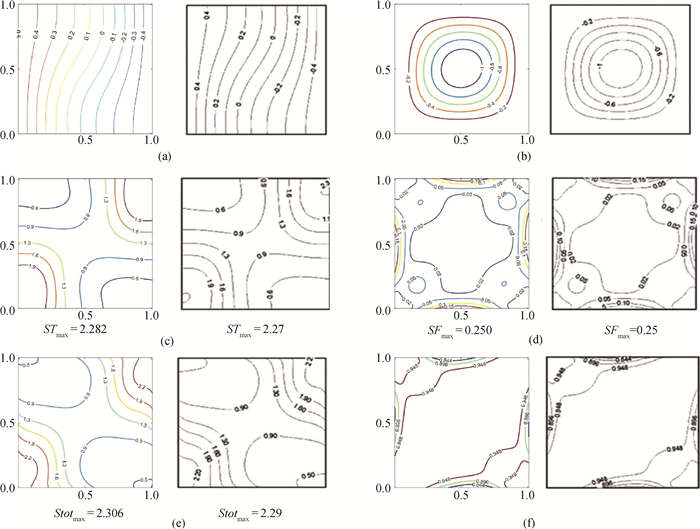
图2 本文结果(左)与Ilis等[37]结果(右) (a) 温度场；(b) 流场；(c) ST；(d) SF；(e) Stot；(f) Be

Fig.2 Results of current work (left) and Ilis [37] (right) (a) Isotherms; (b) Streamlines; (c) ST; (d) SF; (e) Stot; (f) Be

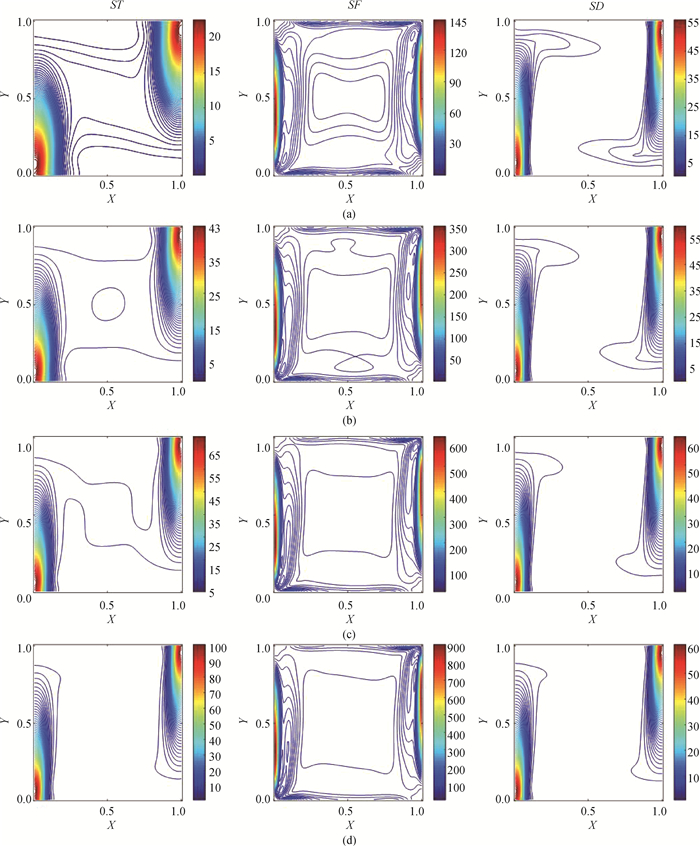
图3 不同ε下，ST、SF、SD的分布(a) ε = 0.3；(b) ε = 0.5；(c) ε = 0.7；(d) ε = 0.9

Fig.3 ST, SF and SD at different ε (a) ε = 0.3; (b) ε = 0.5; (c) ε = 0.7; (d) ε = 0.9

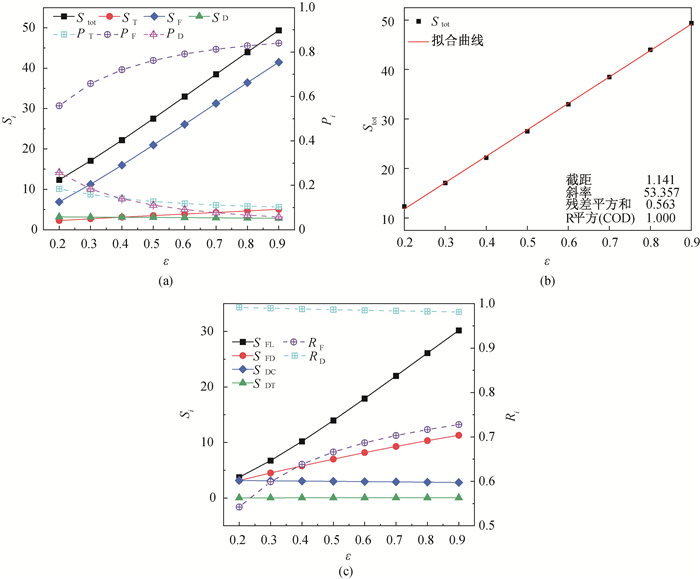
图4 不同ε下，(a) ST、SF、SD、Stot与Pi的分布；(b) Stot随ε变化的拟合曲线；(c) SFL、SFD、SDC、SDT与Ri的变化

Fig.4 (a) ST, SF, SD, Stot and Pi at different ε; (b) A fitting curve of Stot ε; (c) SFL, SFD, SDC, SDT and Ri at different ε

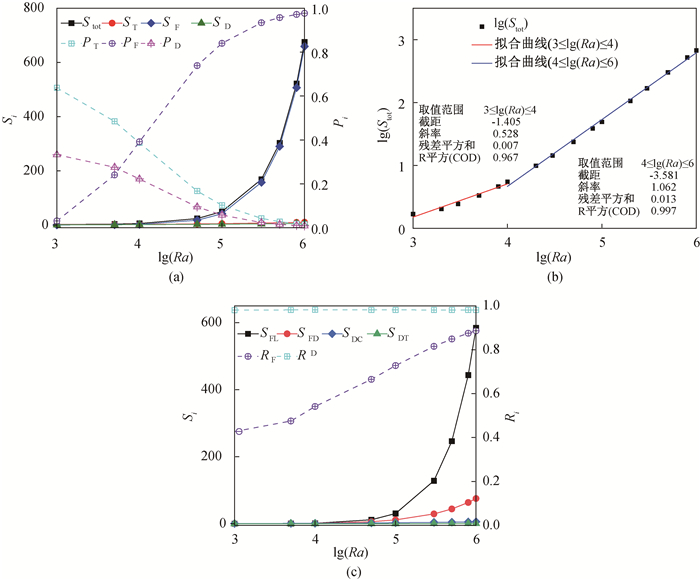
图5 不同Ra下，ST、SF、SD的分布(a) Ra = 103；(b) Ra = 104；(c) Ra = 106

Fig.5 ST, SF and SD at different Ra (a) Ra = 103; (b) Ra = 104; (c) Ra = 106

图6 不同Ra下，(a) ST、SF、SD、Stot与Pi的分布；(b) Stot随Ra变化的拟合曲线；(c) SFL、SFD、SDC、SDT与Ri的变化

Fig.6 (a) ST, SF, SD, Stot and Pi at different Ra; (b) fitting curve of Stot; (c) SFL, SFD, SDC, SDT and Ri at different Ra

图7 不同Br下，ST、SF、SD的分布(a) Br = 2；(b) Br = 0；(c) Br = - 0.5；(d) Br = - 2

Fig.7 ST, SF and SD at different Br (a) Br = 2; (b) Br = 0; (c) Br = - 0.5; (d) Br = - 2

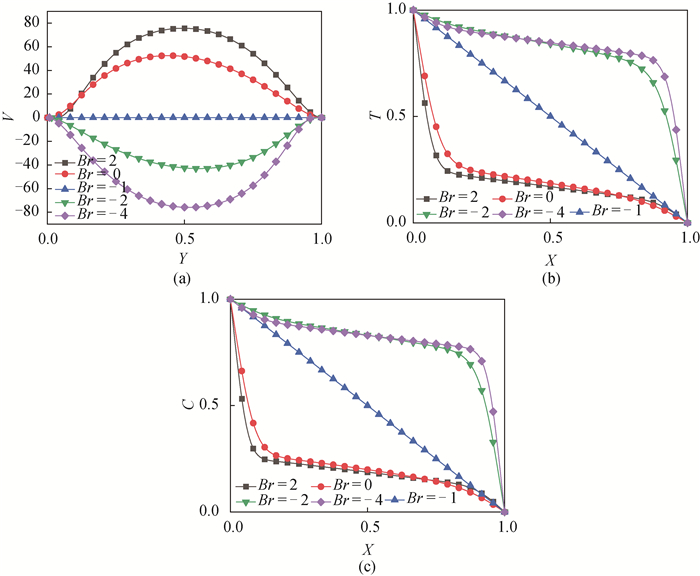
图8 (a) X=0.1处，不同Br下的竖直方向速度；(b) Y = 0.1处，不同Br下的温度与浓度分布

Fig.8 (a) Vertical velocity distribution at X = 0.1; (b) Temperature and concentration distribution at Y = 0.1 at different Br

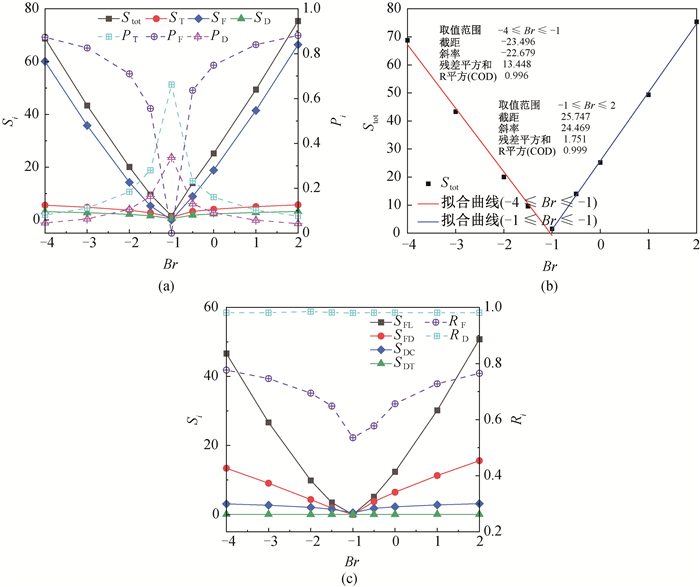
图9 不同Br下，(a) ST、SF、SD、Stot与Pi的分布；(b) Stot随Br变化的拟合曲线；(c) SFL、SFD、SDC、SDT与Ri的变化

Fig.9 (a) ST, SF, SD, Stot and Pi at different Br; (b) A fitting curve of Stot; (c) SFL, SFD, SDC, SDT and Ri at different Br

图10 不同γ下，ST、SF、SD的分布(a) γ = 40°；(b) γ = 60°；(c) γ = 80°

Fig.10 ST, SF and SD at different γ (a) γ = 40°; (b) γ = 60°; (c) γ = 80°

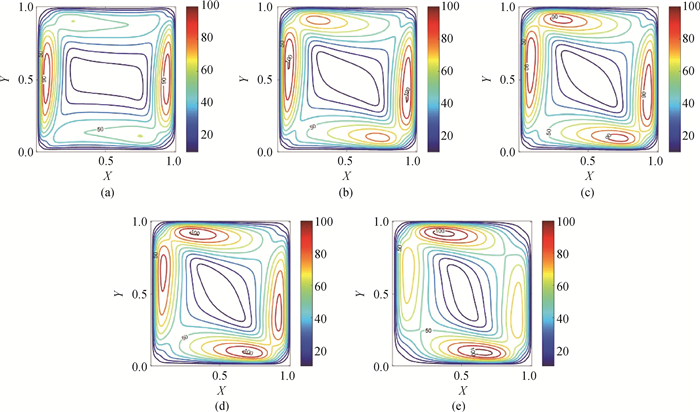
图11 不同γ下的速度场(a) γ = 20°；(b) γ = 40°；(c) γ = 50°；(d) γ = 60°；(e) γ = 80°

Fig.11 Velocity Field for different γ (a) γ = 20°; (b) γ = 40°; (c) γ = 50°; (d) γ = 60°; (e) γ = 80°

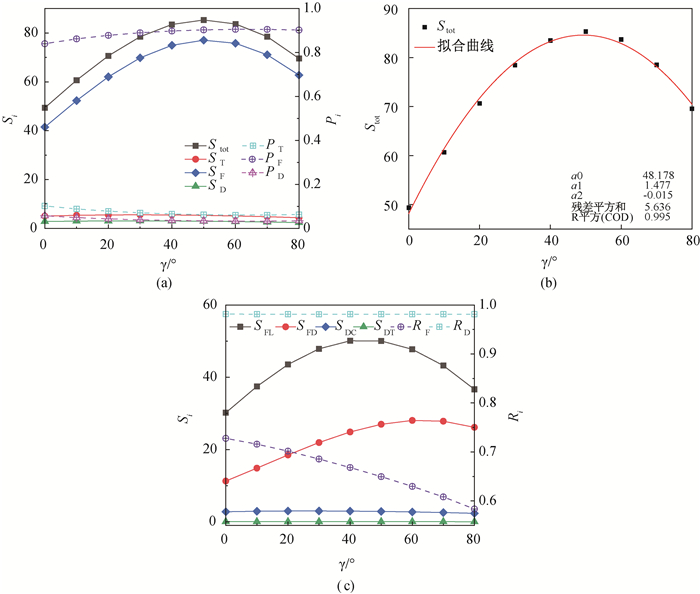
图12 不同γ下，(a) ST、SF、SD、Stot与Pi的分布；(b) Stot随γ变化的拟合曲线；(c) SFL、SFD、SDC、SDT与Ri的变化

Fig.12 (a) ST, SF, SD, Stot and Pi at different γ; (b) A fitting curve of Stot and γ; (c) SFL, SFD, SDC, SDT and Ri at different γ

参考文献 37

1	TURNER J S . Double-diffusive phenomena[J]. Annual Review of Fluid Mechanics, 1974, 6, 37- 54. DOI
2	刘芳, 陈宝明. 多孔介质对室内有机挥发物扩散的影响[J]. 山东建筑大学学报, 2012, 27 (2): 160- 163. DOI
3	RAGUI K , BOUTRA A , BENKAHLA Y K . On the validity of a numerical model predicting heat and mass transfer in porous square cavities with a bottom thermal and solute source: Case of pollutants spreading and fuel leaks[J]. Mechanics & Industry, 2016, 17 (3): 311- 311.
4	HADIDI N , OULD-AMER Y , BENNACER R . Bi-layered and inclined porous collector: Optimum heat and mass transfer[J]. Energy, 2013, 51 (1): 422- 430.
5	FENG L L , XU H T , WANG D , et al. Lattice Boltzmann simulation of formaldehyde adsorption by activated carbon[J]. Chinese Journal of Computational Physics, 2021, 38 (1): 69- 78.
6	LUO Z Q , LOU Q , XU H T , et al. LBM simulation of heat and mass double diffusion: Fluid-solid conjugate heat transfer and adsorption[J]. Chinese Journal of Computational Physics, 2019, 36 (1): 60- 68.
7	SHAO Q , FAHS M , YOUNES A , et al. A high-accurate solution for Darcy-Brinkman double-diffusive convection in saturated porous media[J]. Numerical Heat Transfer, Part B: Fundamentals, 2016, 69 (1): 26- 47. DOI
8	ALY A M , ASAI M . ISPH method for double-diffusive natural convection under cross-diffusion effects in an anisotropic porous cavity/annulus[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2016, 26 (1): 235- 268.
9	BADRUDDIN I A, KHAN T, SAN J, et al. Effect of variable heating on double diffusive flow in a square porous cavity[C]. AIP Conference Proceedings, 2016, 1728(1): 020689.
10	SABERI A , NIKBAKHTI R . Numerical investigation of double-diffusive natural convection in a rectangular porous enclosure with partially active thermal walls[J]. Journal of Porous Media, 2016, 19 (3): 259- 275. DOI
11	WANG J , LOU Q , XU H T , et al. Lattice Boltzmann simulation of double diffusive natural convection in an enclosure with Soret and Dufour effects[J]. Chinese Journal of Computational Physics, 2018, 35 (4): 405- 412.
12	KEFAYATI G R , TANG H , CHAN A , et al. A lattice Boltzmann model for thermal non-Newtonian fluid flows through porous media[J]. Computers & Fluids, 2018, 176 (15): 226- 244.
13	KEFAYATI G . Lattice Boltzmann simulation of double-diffusive natural convection of viscoplastic fluids in a porous cavity[J]. Physics of Fluids, 2019, 31 (1): 013105- 013105. DOI
14	SHAO Q , FAHS M , YOUNES A , et al. A new benchmark reference solution for double-diffusive convection in heterogeneous porous medium[J]. Numerical Heat Transfer, Part B: Fundamentals, 2016, 70 (5): 373- 392. DOI
15	CHEN S , YANG B , ZHENG C . Simulation of double diffusive convection in fluid-saturated porous media by lattice Boltzmann method[J]. International Journal of Heat & Mass Transfer, 2017, 108 (Pt.B): 1501- 1510.
16	HE B Y , LU S H , GAO D Y , et al. Lattice Boltzmann simulation of double diffusive natural convection in heterogeneously porous media of a fluid with temperature-dependent viscosity[J]. Chinese Journal of Physics, 2020, 63, 186- 200. DOI
17	NG T , SU Y . Non-dimensional lattice Boltzmann simulations on pore scale double diffusive natural convection in an enclosure filled with random porous media[J]. International Journal of Heat and Mass Transfer, 2019, 134, 521- 538. DOI
18	BEJAN A . Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes[J]. Journal of Applied Physics, 1996, 79 (3): 1191- 1218. DOI
19	BISWAL P , BASAK T . Entropy generation vs energy efficiency for natural convection based energy flow in enclosures and various applications: A review[J]. Renewable & Sustainable Energy Reviews, 2017, 80, 1412- 1457.
20	COSTA V . On natural convection in enclosures filled with fluid-saturated porous media including viscous dissipation[J]. International Journal of Heat and Mass Transfer, 2005, 49 (13): 2215- 2226.
21	BISWAL P , NAG A , BASAK T . Analysis of thermal management during natural convection within porous tilted square cavities via heatline and entropy generation[J]. International Journal of Mechanical Sciences, 2016, 115-116, 596- 615. DOI
22	DATTA P , MAHAPATRA P S , GHOSH K , et al. Heat transfer and entropy generation in a porous square enclosure in presence of an adiabatic block[J]. Transport in Porous Media, 2016, 111 (2): 305- 329. DOI
23	MCHIRGUI A , HIDOURI N , MAGHERBI M , et al. Entropy generation in double-diffusive convection in a square porous cavity using Darcy-Brinkman formulation[J]. Transport in Porous Media, 2012, 93 (1): 223- 240. DOI
24	MCHIRGUI A , HIDOURI N , MAGHERBI M , et al. Second law analysis in double diffusive convection through an inclined porous cavity[J]. Computers & Fluids, 2014, 96 (13): 105- 115.
25	ANANDALAKSHMI R , BASAK T . Analysis of energy management via entropy generation approach during natural convection in porous rhombic enclosures[J]. Chemical Engineering Science, 2012, 79 (10): 75- 93.
26	BOUABID M , GHOUDI N , BOUABDA R , et al. Irreversibility analysis for double diffusive convection flow of a gas mixture in a chamfered corners square enclosure filled with a porous medium[J]. Arabian Journal for Science and Engineering, 2020, 45 (9): 7499- 7510. DOI
27	SIAVASHI M , BORDBAR V , RAHNAMA P . Heat transfer and entropy generation study of non-Darcy double-diffusive natural convection in inclined porous enclosures with different source configurations[J]. Applied Thermal Engineering, 2017, 110 (5): 1462- 1475.
28	NITHYADEVI N , RAJARATHINAM M , SURESH N . Density maximum effect of double-diffusive mixed convection heat transfer in a two-sided lid-driven porous cavity[J]. Special Topics & Reviews in Porous Media: An International Journal, 2017, 8 (3): 245- 261.
29	BAO T , LIU Z . Thermohaline stratification modeling in mine water via double-diffusive convection for geothermal energy recovery from flooded mines[J]. Applied Energy, 2019, 237 (1): 566- 580.
30	REDDY K S , SREEDHAR D . Thermal conductivity of natural fiber, glass fiber & CNTs reinforced epoxy composites[J]. International Journal of Current Engineering and Technology, 2016, 6 (4): 1196- 1198.
31	BEJAN A . A study of entropy generation in fundamental convective heat transfer[J]. Journal of Heat Transfer, 1979, 101 (4): 718- 725. DOI
32	郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2009: 208- 212.
33	KEFAYATI G . Simulation of double diffusive natural convection and entropy generation of power-law fluids in an inclined porous cavity with Soret and Dufour effects (Part II: Entropy generation)[J]. International Journal of Heat and Mass Transfer, 2016, 94, 582- 624. DOI
34	LAM P , PRAKASH K A . A numerical study on natural convection and entropy generation in a porous enclosure with heat sources[J]. International Journal of Heat & Mass Transfer, 2014, 69, 390- 407.
35	SETA T , TAKEGOSHI E , OKUI K . Lattice Boltzmann simulation of natural convection in porous media[J]. Mathematics & Computers in Simulation, 2006, 72 (2): 195- 200.
36	XU H T , WANG T T , QU Z G , et al. Lattice Boltzmann simulation of the double diffusive natural convection and oscillation characteristics in an enclosure filled with porous medium[J]. International Communications in Heat & Mass Transfer, 2017, 81, 104- 115.
37	ILIS G G , MOBEDI M , SUNDEN B . Effect of aspect ratio on entropy generation in a rectangular cavity with differentially heated vertical walls[J]. International Communications in Heat and Mass Transfer, 2008, 35 (6): 696- 703. DOI

[1]	冯舒婷, 戴厚平, 宋通政. 二维空间分数阶反应扩散方程组的格子Boltzmann方法[J]. 计算物理, 2022, 39(6): 666-676.
[2]	林品亮, 冯欢欢, 董宇红. 具有多孔介质覆面层的柱体绕流流场分析[J]. 计算物理, 2022, 39(4): 418-426.
[3]	张巧玲, 景何仿. 三维曲面腔顶盖驱动流的MRT-LBM研究[J]. 计算物理, 2022, 39(4): 427-439.
[4]	陈露, 高明, 梁佳, 王东民, 赵玉刚, 章立新. 润湿梯度作用下液滴在倾斜表面向上运动的格子Boltzmann模拟[J]. 计算物理, 2021, 38(6): 672-682.
[5]	魏雪丹, 戴厚平, 李梦军, 郑洲顺. 一维空间Riesz分数阶对流扩散方程的格子Boltzmann方法[J]. 计算物理, 2021, 38(6): 683-692.
[6]	蔡建超. 多孔介质自发渗吸关键问题与思考[J]. 计算物理, 2021, 38(5): 505-512.
[7]	郑江韬, 贾宁洪, 胡慧芳, 杨勇, 鞠杨, 王沫然. 分支通道内液-液自发渗吸规律研究[J]. 计算物理, 2021, 38(5): 543-554.
[8]	魏祥祥, 冯其红, 张先敏, 黄迎松, 刘丽杰. 基于VOF方法的水驱油藏孔隙尺度剩余油分布状态研究[J]. 计算物理, 2021, 38(5): 573-584.
[9]	王敏, 申玉清, 陈震宇, 徐鹏. 随机多孔介质的蒙特卡罗重构与渗流特性模拟[J]. 计算物理, 2021, 38(5): 623-630.
[10]	娄钦, 汤升, 王浩原. 基于格子Boltzmann大密度比模型的多孔介质内气泡动力学行为数值模拟[J]. 计算物理, 2021, 38(3): 289-300.
[11]	梁佳, 高明, 陈露, 王东民, 章立新. 液滴撞击不同湿润性固壁面上静止液滴的格子Boltzmann研究[J]. 计算物理, 2021, 38(3): 313-323.
[12]	袁俊杰, 叶欣, 单彦广. 格子Boltzmann方法模拟填充纳米流体三角形腔内的自然对流[J]. 计算物理, 2021, 38(1): 57-68.
[13]	王坚毅, 潘振海, 吴慧英. 微通道内椭球颗粒惯性聚焦行为数值研究[J]. 计算物理, 2020, 37(6): 677-686.
[14]	万启坤, 罗松, 尚文强, 张莹, 刘昊天, 朱宝杰. 不连续冷源布局多孔介质内热流耦合LBM数值模拟[J]. 计算物理, 2020, 37(4): 431-438.
[15]	冯其红, 赵蕴昌, 王森, 张以根, 孙业恒, 史树彬. 基于相场方法的孔隙尺度油水两相流体流动模拟[J]. 计算物理, 2020, 37(4): 439-447.