基于复杂网络理论的电网耦合强度分配策略

doi:10.19596/j.cnki.1001-246x.8500

摘要/Abstract

摘要：

为探究提高电网性能的线路耦合强度分配方法, 用临界同步耦合强度描述电网的同步能力, 通过对网络节点施加扰动功率的方式攻击电网来分析其动态鲁棒性。研究发现: 电网节点的局部拓扑结构和功率约束着节点的局部同步能力。一般情况下, 节点功率越大, 度值越小, 它的局部同步能力就越弱, 该节点与其邻居节点就越难达到局部同步状态。基于节点的局部同步能力, 提出一种输电线路耦合强度的非均匀分配策略, 即在网络总耦合强度不变的情况下, 适当增大局部同步能力较弱节点间线路的耦合强度, 减小局部同步能力较强节点间线路的耦合强度。研究表明: 这种方法可以在一定程度上优化网络的同步能力, 增强电网的鲁棒性。

关键词: 电网, 耦合强度, 同步, 鲁棒性

Abstract:

To explore allocation strategy of network coupling strength for improving performance of power grids, we analyze synchronizability of power grids by using critical synchronization coupling strength, and compare robustness of power grids by imposing disturbance power on network nodes. It is found that local topological structure and power of nodes in power grids restrict the local synchronizability of nodes. In general, the greater the power and the smaller the degree value of the node, the weaker its local synchronizability is. And it is more difficult for the node to reach a local synchronization state with its neighbors. Based on this, a non-uniform distribution strategy of network coupling strength is proposed. Keep the total coupling strength the same, we increase the coupling strength between nodes with weak local synchronizability, and reduce the coupling strength between nodes with strong local synchronizability. It shows that this method optimizes synchronizability of the network and enhance robust performance of power grids to a certain extent.

Key words: power grids, coupling strength, synchronization, robustness

高正, 邹艳丽, 胡均万, 姚高华, 刘唐慧美. 基于复杂网络理论的电网耦合强度分配策略[J]. 计算物理, 2022, 39(5): 579-588.

Zheng GAO, Yanli ZOU, Junwan HU, Gaohua YAO, Tanghuimei LIU. Coupling Strength Allocation Strategy in Power Grids Based on Complex Network Theory[J]. Chinese Journal of Computational Physics, 2022, 39(5): 579-588.

图/表 9

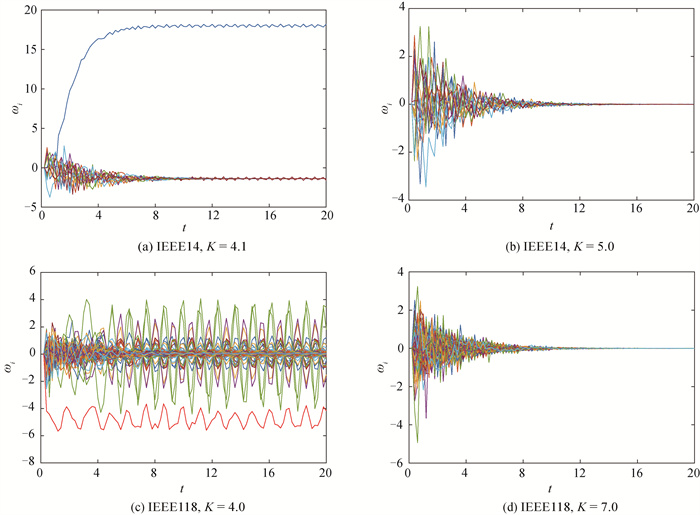
图1 IEEE标准测试系统的网络频偏随演化时间变化(a)、(c) IEEE14和IEEE118系统的网络频偏向高频振荡和低频振荡两个集群进行发散；(b)、(d) IEEE14和IEEE118系统的网络频偏向标准工作频率进行汇聚

Fig.1 Frequency offset varies with evolution time in IEEE standard test systems (a) and (c) Divergence of frequency offset towards two clusters at high and low oscillating frequencies before network synchronization in IEEE14 and IEEE118 systems; (b) and (d) Convergence of frequency offset towards common frequency in IEEE14 and IEEE118 systems

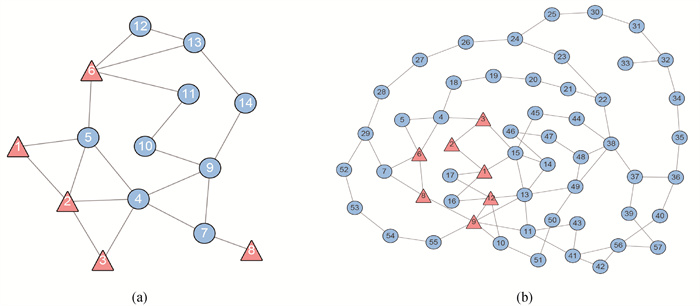
图2 EEE标准测试网络拓扑结构 (品红色三角形表示发电机节点, 蓝色圆形表示负载节点。)(a) IEEE14标准测试网络; (b) IEEE57标准测试网络

Fig.2 Topology of IEEE standard test systems (Pink triangles denote generators. Blue circles denote consumers.)(a) IEEE14 standard test system; (b) IEEE57 standard test system

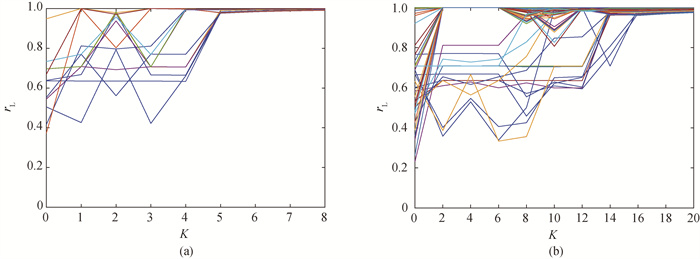
图3 局部平均序参数随耦合强度的变化 (蓝色粗线代表发电机节点, 其它颜色折线代表负载节点。)(a) IEEE14标准测试网络; (b) IEEE57标准测试网络

Fig.3 Local order parameter varies with coupling strength (The blue and bold lines represent the generator nodes. Other lines represent the load nodes.)(a) IEEE14 standard test system; (b) IEEE57 standard test system

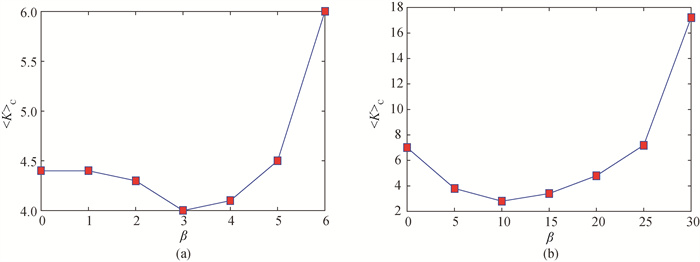
图4 网络的临界同步耦合强度均值随线路耦合强度离散率的变化(a) IEEE14标准测试网络; (b) IEEE118标准测试网络

Fig.4 Critical synchronous coupling strength varies with line coupling strength dispersion rate in IEEE systems (a) IEEE14 standard test system; (b) IEEE118 standard test system

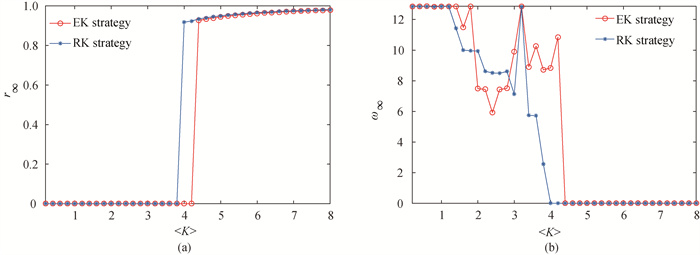
图5 IEEE14节点系统(a)稳态序参数, (b)平均频偏随平均耦合强度的变化

Fig.5 (a) Steady-state order parameter and (b) average frequency offset vary with average coupling strength in an IEEE14 system

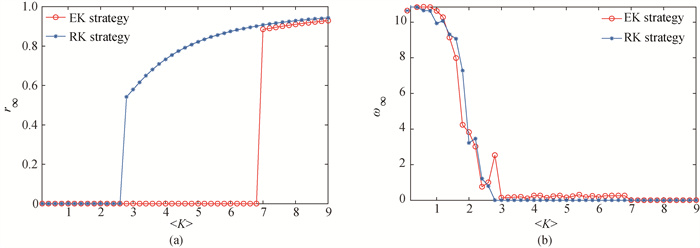
图6 IEEE118节点系统(a)稳态序参数, (b)平均频偏随平均耦合强度的变化

Fig.6 (a) Steady-state order parameter and (b) average frequency offset vary with average coupling strength in an IEEE118 system

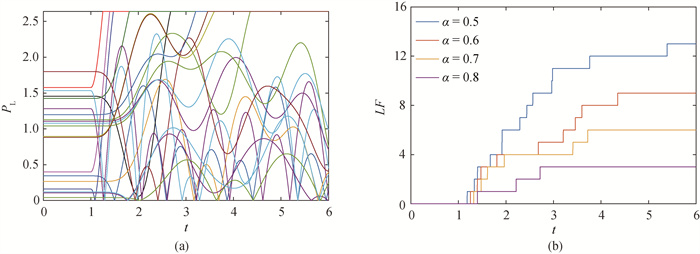
图7 IEEE14节点系统(a)各线路的传输功率, (b)失效连边总数随演化时间的变化

Fig.7 (a) Transmission power of each line and (b) number of failed lines vary with evolution time in IEEE14 system

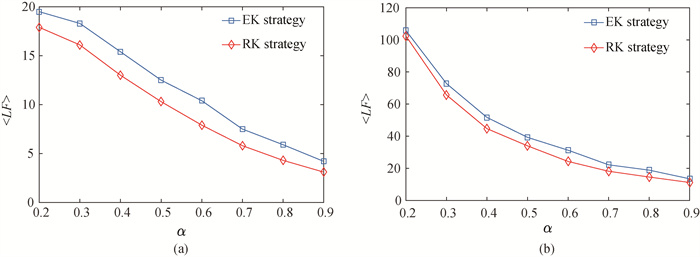
图8 IEEE网络中平均失效线路总数随容量控制参数的变化(a) IEEE14标准测试网络; (b) IEEE118标准测试网络

Fig.8 Average number of failed lines varies with control parameter in IEEE systems (a) IEEE14 standard test system; (b) IEEE118 standard test system

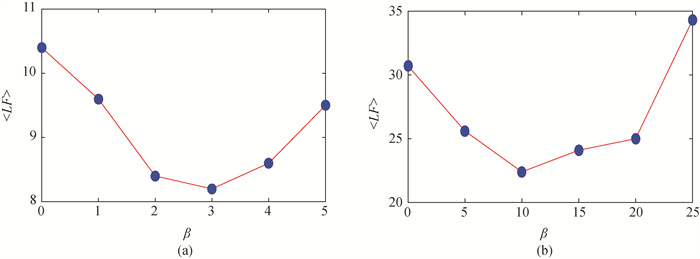
图9 IEEE网络中平均失效线路总数随线路耦合强度离散率的变化(a) IEEE14标准测试网络; (b) IEEE118标准测试网络

Fig.9 Average number of failed lines varies with line coupling strength dispersion rate in IEEE systems (a) IEEE14 standard test system; (b) IEEE118 standard test system

参考文献 28

1	STROGATZ S H . Exploring complex networks[J]. Nature, 2001, 410 (6825): 268- 276. DOI
2	PAGANI G A , AIELLO M . From the grid to the smart grid, topologically[J]. Physica A, 2016, 449, 160- 175. DOI
3	RODRIGUES F A , PERON T , JI P , et al. The Kuramoto model in complex networks[J]. Physics Reports, 2016, 610, 1- 98. DOI
4	汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用[M]. 北京: 清华大学出版社, 2006.
5	ZOU Y L , CHEN G R . Choosing effective controlled nodes for scale-free network synchronization[J]. Physica A: Statistical Mechanics & Its Applications, 2009, 388 (14): 2931- 2940.
6	孔江涛, 黄健, 龚建兴, 等. 基于复杂网络动力学模型的无向加权网络节点重要性评估[J]. 物理学报, 2018, 67 (9): 98901- 098901.
7	ZOU Y L , WANG R R , GAO Z . Improve synchronizability of a power grid through power allocation and topology adjustment[J]. Physica A: Statistical Mechanics and Its Applications, 2020, 548, 122956. DOI
8	LI H Q , ZOU Y L , ZHANG S Z , et al. Robustness of power grids structure and Braess paradox phenomenon: A complex network theory study[J]. Chinese Journal of Computational Physics, 2021, 38 (4): 470- 478.
9	LUCIA V G , ARTURO B , LUIGI F , et al. Analysis of dynamical robustness to noise in power grids[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2017, 7 (3): 413- 421. DOI
10	胡钋, 李莉莉, 张宝丹, 等. 智能电网中交互级联故障传播的影响因素分析[J]. 智慧电力, 2021, 49 (5): 69- 76. DOI
11	ZHANG G , LI Z , ZHANG B , et al. Understanding the cascading failures in Indian power grids with complex networks theory[J]. Physica A, 2013, 392, 3273- 3280. DOI
12	王宇飞, 李俊娥, 刘艳丽, 等. 容忍阶段性故障的协同网络攻击引发电网级联故障预警方法[J]. 电力系统自动化, 2021, 45 (3): 24- 32.
13	ZHU Q , ZHU Z , QI Y , et al. Optimization of cascading failure on complex network based on NNIA[J]. Physica A: Statistical Mechanics & Its Applications, 2018, 501, 42- 51.
14	TOMMASO N , ALESSANDRO Z , BERT Z . Emergent failures and cascades in power grids: A statistical physics perspective[J]. Physical Review Letters, 2018, 120 (25): 258301. DOI
15	ZHANG X , ZHAN C , TSE C K . Modeling the dynamics of cascading failures in power systems[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2017, 192- 204.
16	YANG L X , JIANG J . Impacts of link addition and removal on synchronization of an elementary power network[J]. Physica A, 2017, 479, 99- 107. DOI
17	ZOU Y L , GAO Z , LIANG M Y , et al. Optimization of synchronization performance and robustness analysis in power grids based on power tracing,[J]. Chinese Journal of Computational Physics, 2020, 37 (5): 623- 630.
18	BANDYOPADHYAY A , KAR S . Impact of network structure on synchronization of Hindmarsh-Rose neurons coupled in structured network[J]. Applied Mathematics and Computation, 2018, 333, 194- 212. DOI
19	CHEN Z H , WU J J , XIA Y X , et al. Robustness of interdependent power grids and communication networks: A complex network perspective[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2018, 65 (1): 115- 119. DOI
20	刘文霞, 黄钰辰, 万海洋, 等. 复杂网络理论在能源互联网脆弱性与鲁棒性研究中的应用[J]. 智慧电力, 2021, 49 (1): 14- 21. DOI
21	傅杰, 邹艳丽, 谢蓉. 基于复杂网络理论的电力网络关键线路识别[J]. 复杂系统与复杂性科学, 2017, 14 (3): 91- 96.
22	KUMAWAT M , GUPTA N , JAIN N , et al. Optimally allocation of distributed generators in three-phase unbalanced distribution network[J]. Energy Procedia, 2017, 142, 749- 754. DOI
23	ZOU Y L , WANG R R , WU L J , et al. Optimization of synchronization performance in power grids with local order parameters[J]. Chinese Journal of Computational Physics, 2019, 36 (4): 498- 504.
24	FILATRELL A G , NIELSEN A H , PEDERSENN F . Analysis of a power grid using a Kuramoto-like model[J]. European Physical Journal B, 2008, 61 (4): 485- 491. DOI
25	ROHDEN M , SORGE A , WITTHAUT D , et al. Impact of network topology on synchrony of oscillatory power grids[J]. Chaos, 2013, 24 (1): 586.
26	ZHANG X , BOCCALETTI S , GUAN S , et al. Explosive synchronization in adaptive and multilayer networks[J]. Physical Review Letters, 2015, 114 (3): 038701. DOI
27	GUO L , ZHANG W Y , LUO Z J , et al. A dynamical approach to identify vertices' centrality in complex networks[J]. Physics Letters A, 2017, 381 (48): 3972- 3977. DOI
28	SCHFER B , WITTHAUT D , TIMME M , et al. Dynamically induced cascading failures in power grids[J]. Nature Communications, 2018, 9 (1): 1- 13.

[1]	刘凯歌, 韦笃取. 基于WOA-ESN的电机系统混沌振荡预测[J]. 计算物理, 2022, 39(4): 498-504.
[2]	张少泽, 邹艳丽, 谭秫毅, 李浩乾, 刘欣妍. 基于复杂网络理论的互联电网Braess悖论现象分析[J]. 计算物理, 2022, 39(2): 233-243.
[3]	邹艳丽, 高正, 梁明月, 李志慧, 何铭. 基于潮流追踪的电网同步性能优化及鲁棒性分析[J]. 计算物理, 2020, 37(5): 623-630.
[4]	石建平, 李培生, 刘国平. 基于改进克隆选择算法的统一混沌系统同步控制与参数辨识[J]. 计算物理, 2020, 37(2): 240-252.
[5]	钟国翔, 韦笃取, 张波. 分布式发电系统感性负载的远程混沌同步[J]. 计算物理, 2019, 36(6): 719-725.
[6]	邹艳丽, 王瑞瑞, 吴凌杰, 姚飞, 汪洋. 基于局部序参数的电网同步性能优化[J]. 计算物理, 2019, 36(4): 498-504.
[7]	石建平, 杨兰天, 刘丹. 基于量子粒子群算法的混沌系统同步控制及参数辨识[J]. 计算物理, 2019, 36(2): 236-244.
[8]	查进道, 李春彪. 基于引力场理论的混沌同步[J]. 计算物理, 2018, 35(6): 737-749.
[9]	刘利花, 韦笃取, 张波. 基于动力中继的小世界复杂电机网络混沌同步控制[J]. 计算物理, 2018, 35(6): 750-756.
[10]	王意, 邹艳丽, 黄李, 李可. 综合考虑局部和全局特性的电网关键节点识别[J]. 计算物理, 2018, 35(1): 119-126.
[11]	钱慧, 于洪洁. SC混沌比例投影同步方法在保密通信中的应用[J]. 计算物理, 2016, 33(1): 117-126.
[12]	蓝庆玉, 邹艳丽, 冯聪. 电网在三种边攻击方式下的级联失效[J]. 计算物理, 2012, 29(6): 943-948.
[13]	孟娟, 王兴元. 一类延迟混沌神经网络的鲁棒反同步[J]. 计算物理, 2008, 25(2): 247-252.
[14]	冯秀琴, 沈柯. 利用超混沌信号调制参数实现简并光学参量振荡器混沌同步[J]. 计算物理, 2007, 24(6): 677-682.
[15]	于洪洁, 彭建华. 非线性耦合超混沌Rössler系统和网络的同步[J]. 计算物理, 2006, 23(5): 626-630.