计算物理 ›› 2023, Vol. 40 ›› Issue (1): 117-126.DOI: 10.19596/j.cnki.1001-246x.8552
• 研究论文 • 上一篇
收稿日期:2022-04-28
出版日期:2023-01-25
发布日期:2023-07-04
通讯作者:
邓敏艺
作者简介:李成乾(1995-),男,硕士研究生,主要研究方向为激发介质的螺旋波动力学,E-mail: gxsdlichengqian@163.com
基金资助:
Chengqian LI( ), Furong GUAN, Minyi DENG*(
), Furong GUAN, Minyi DENG*( )
)
Received:2022-04-28
Online:2023-01-25
Published:2023-07-04
Contact:
Minyi DENG
摘要:
采用元胞自动机模型研究传导速度恢复关系导致的传导阻滞与折返效应及其对螺旋波演化行为的影响,发现稳定螺旋波的形状、螺旋波的爱克豪斯失稳及多普勒失稳均与传导阻滞及折返效应有关:稳定螺旋波呈现内凹形是因为系统沿各方向的阻滞程度不同,呈菱形是因为所有元胞沿斜向传导的电信号都被严重阻滞;螺旋波的爱克豪斯失稳源于螺旋波外围存在较强的传导阻滞及因此导致的电信号折返,两者共同作用造成开始于外围的波臂断裂;螺旋波的多普勒失稳产生于出现在波头附近的较强传导阻滞,这种传导阻滞使波头附近的波臂沿某个方向挤压而沿另外方向拉伸,导致开始于波头附近的波臂断裂。本研究从细胞水平和电信号传导角度解释螺旋波不同演化行为的产生原因。
李成乾, 关富荣, 邓敏艺. 传导阻滞和折返效应对螺旋波演化行为的影响[J]. 计算物理, 2023, 40(1): 117-126.
Chengqian LI, Furong GUAN, Minyi DENG. Effects of Conduction Block and Reentry on Evolution of Spiral Waves[J]. Chinese Journal of Computational Physics, 2023, 40(1): 117-126.
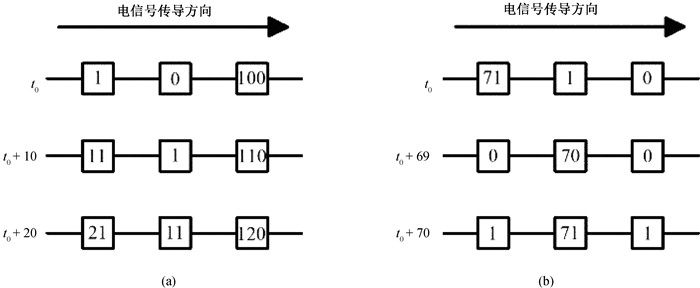
图1 传导阻滞与折返效应的产生示例(a)传导阻滞,(b)折返效应(方框及框内的数字分别代表元胞及元胞的状态值。)
Fig.1 Examples of the emergence of (a) conduction block and (b) reentry (The square frames and the figures represent cells and their state values, respectively.)
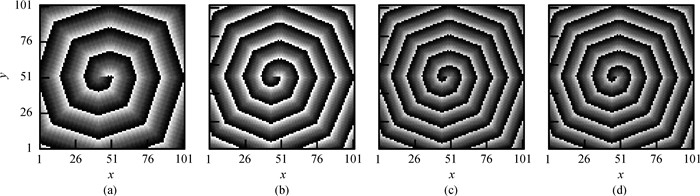
图2 不考虑CVR, t=30 000时的螺旋波斑图,γ=2 (a)α=2 300, β=34;(b) α=1 400, β=40;(c)α=1 500, β=40; (d)α=2 600, β=36(斑图中白色、黑色和灰色分别代表元胞处于静息态、激发态和不应态,其中灰色越深代表不应态的状态值越小。)
Fig.2 Patterns of stable spiral waves without CVR at t=30 000 and γ=2 (a)α=2 300, β=34;(b)α=1 400, β=40; (c)α=1 500, β=40; (d)α=2 600, β=36(The white, dark and gray represent the state of rest, excited and refractory, respectively. Deeper gray indicates smaller value of refractory state.)

图3 考虑CVR后,螺旋波内凹与传导阻滞的关系(a)~(c)螺旋波演化过程中的时空斑图;(d)~(f)内凹区域的局部状态分布图;(g)~(i)非内凹区域的局部状态分布图(状态分布图中方框及数字的意义同图 1,斑图中的不同颜色意义同图 2,圆圈代表关注的元胞,箭头末端所在代表电信号到达地点,箭头始端所在代表电信号来源地点。参数见图 2(a)。)
Fig.3 The concave shape of spiral wave due to CVR and its relation with conduction block (a)~(c)spiral wave patterns; (d)~(f)local state distributions in concave region; (g)~(i)local state distributions in non-concave region (The square frames and figures in local state distributions are the same as in Fig. 1. Colors in patters represent the same as in Fig. 2. The cell with attention is signed with a circle. The end of arrow is at the point where electrical signal arrives, and beginning of the arrow is the source of electrical signal. Parameters are the same as in Fig. 2(a).)
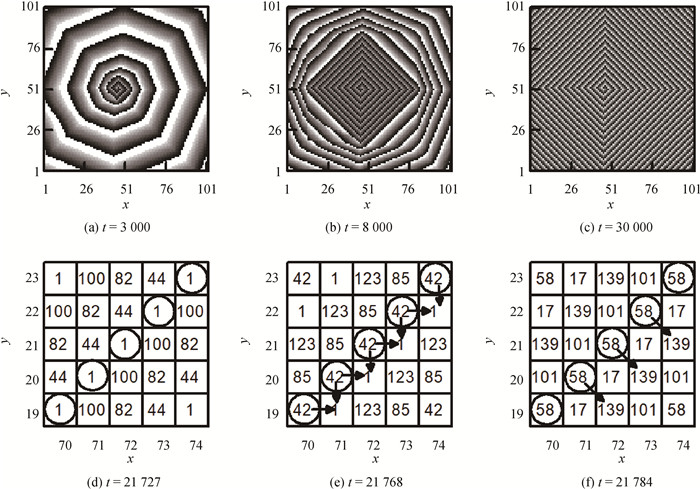
图4 考虑CVR后,螺旋波呈菱形与传导阻滞的关系(a)~(c)菱形螺旋波形成过程中的时空斑图;(d)~(f)对角线方向的电信号被阻滞的局部状态分布(斑图中颜色以及状态分布图中符号所代表的意义同图 3。参数见图 2(b)。)
Fig.4 Rhombic shape of spiral wave due to CVR and its relation with conduction block (a)~(c)spiral wave patterns; (d)~(f) local state distributions reflecting conduction blocks along the diagonal direction (Colors in patterns and signals in state distributions represent the same as in Fig. 3. Parameters are the same as in Fig. 2(b).)

图5 考虑CVR后,螺旋波爱克豪斯失稳及其与传导阻滞和折返效应的关系(a)、(b)螺旋波爱克豪斯失稳过程中的时空斑图;(c)、(d)发生阻滞的局部状态分布;(e)、(f)发生折返的局部状态分布(斑图中颜色以及状态分布图中符号所代表的意义同图 3。参数见图 2(c)。)
Fig.5 Eckhaus instability due to CVR and its relation with conduction block and reentry (a) and (b) patterns during Eckhaus instability process; (c) and (d) local state distributions reflecting the conduction block; (e) and (f) local state distributions reflecting the reentry (Colors in patters and signals in state distributions represent the same as in Fig. 3. Parameters are the same as in Fig. 2(c).)
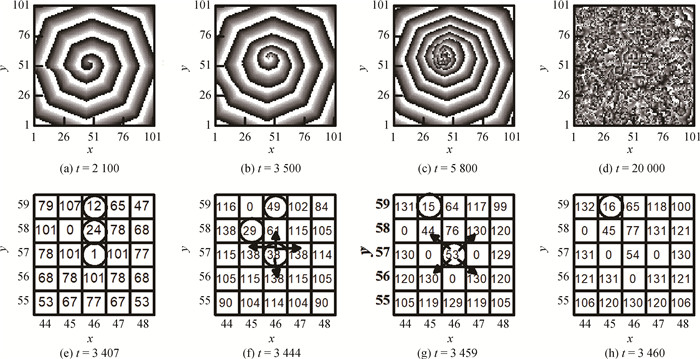
图6 考虑CVR后,螺旋波多普勒失稳及其与传导阻滞的关系(a)~(d)螺旋波失稳过程中的时空斑图;(e)~(h)发生传导阻滞的局部状态分布(斑图中颜色以及状态分布图中符号所代表的意义同图 3。参数见图 2(d)。)
Fig.6 Doppler instability due to CVR and its relation with conduction block (a)~(d)patterns during Doppler instability process; (e)~(h)local state distributions reflecting the conduction block (Colors in patter and signals in state distributions represent the same as in Fig. 3. Parameters are the same as in Fig. 2(d).)
| 单位距离传导时间 | 激发正向邻居 | 激发斜向邻居 |
| 40 | 失败 | 成功 |
| 35 | 成功 | 失败 |
| 37 | 成功 | 失败 |
| 24 | 失败 | 失败 |
| 21 | 失败 | 失败 |
| 21 | 失败 | 成功 |
表1 位于图 3内凹区中(69, 77)的元胞电信号传导时间及其对邻居的激发情况
Table 1 Conduction time of a pulse from a cell at (69, 77) in Fig. 3 and excitation situation of its neighbors
| 单位距离传导时间 | 激发正向邻居 | 激发斜向邻居 |
| 40 | 失败 | 成功 |
| 35 | 成功 | 失败 |
| 37 | 成功 | 失败 |
| 24 | 失败 | 失败 |
| 21 | 失败 | 失败 |
| 21 | 失败 | 成功 |
| 单位距离传导时间 | 激发正向邻居 | 激发斜向邻居 |
| 27 | 成功 | 成功 |
| 27 | 成功 | 成功 |
| 29 | 成功 | 失败 |
| 30 | 成功 | 失败 |
| 30 | 成功 | 失败 |
| 28 | 成功 | 成功 |
表2 位于图 3非内凹区中(46, 84)的元胞电信号传导时间及其对邻居的激发情况
Table 2 Conduction time of a pulse from a cell at (46, 84) in Fig. 3 and excitation situation of its neighbors
| 单位距离传导时间 | 激发正向邻居 | 激发斜向邻居 |
| 27 | 成功 | 成功 |
| 27 | 成功 | 成功 |
| 29 | 成功 | 失败 |
| 30 | 成功 | 失败 |
| 30 | 成功 | 失败 |
| 28 | 成功 | 成功 |
| 单位距离传导时间 | 激发正向邻居 | 激发斜向邻居 |
| 24 | 失败 | 失败 |
| 45 | 成功 | 成功 |
| 41 | 成功 | 失败 |
| 43 | 成功 | 失败 |
| 38 | 成功 | 失败 |
表3 位于图 4中(75, 71)的元胞电信号传导时间及其对邻居的激发情况
Table 3 Conduction time of a pulse from a cell at (75, 71) in Fig. 4 and excitation situation of its neighbors
| 单位距离传导时间 | 激发正向邻居 | 激发斜向邻居 |
| 24 | 失败 | 失败 |
| 45 | 成功 | 成功 |
| 41 | 成功 | 失败 |
| 43 | 成功 | 失败 |
| 38 | 成功 | 失败 |
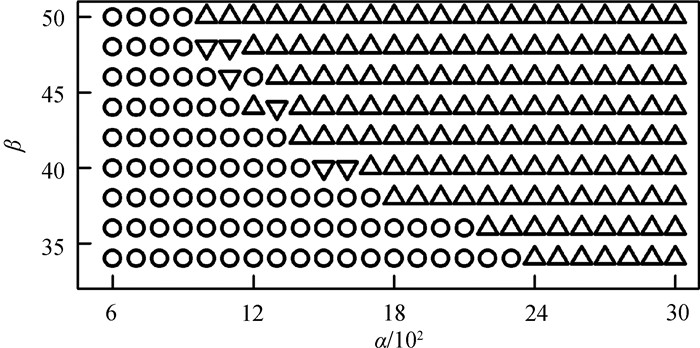
图7 考虑CVR,不同参数下的螺旋波演化结果(〇代表螺旋波稳定,▽代表爱克豪斯失稳,△代表多普勒失稳。)
Fig.7 Evolution types of spiral waves under different parameters as CVR is considered (〇, ▽and △ represent stable spiral waves, Eckhaus instability and Doppler instability, respectively.)
| 1 |
DOI |
| 2 |
|
| 3 |
DOI |
| 4 |
DOI |
| 5 |
|
| 6 |
DOI |
| 7 |
DOI |
| 8 |
DOI |
| 9 |
DOI |
| 10 |
DOI |
| 11 |
DOI |
| 12 |
|
| 13 |
董力耘, 陈立, 段晓茵. 基于教室人群疏散实验的行人流建模和模拟[J]. 物理学报, 2015, 64 (22): 220505.
DOI |
| 14 |
DOI |
| 15 |
|
| 16 |
DOI |
| 17 |
|
| 18 |
DOI |
| 19 |
|
| 20 |
DOI |
| 21 |
张学良, 谭惠丽, 白克钊, 等. 一种体现心肌细胞传导记忆的元胞自动机模型[J]. 广西师范大学学报(自然科学版), 2017, 35 (4): 1- 9.
|
| 22 |
DOI |
| 23 |
欧阳颀. 反应扩散系统中螺旋波的失稳[J]. 物理, 2001, 30 (1): 30- 36.
|
| [1] | 王国威, 付燕. 随机边界诱导Izhikevich神经元网络的时空模式转换[J]. 计算物理, 2023, 40(5): 622-632. |
| [2] | 陈绍英, 王雪丽, 高志梅, 袁国勇. 环域反馈下复Ginzburg-Landau系统的螺旋波动力学行为[J]. 计算物理, 2022, 39(1): 118-126. |
| [3] | 杜丹, 李帅, 阳璞琼, 冯军, 向东, 龚学余. 螺旋天线轴向长度对螺旋波传播、吸收的影响[J]. 计算物理, 2021, 38(6): 713-721. |
| [4] | 关富荣, 李成乾, 邓敏艺. 激发介质相对不应态对螺旋波动力学行为的影响[J]. 计算物理, 2021, 38(6): 749-756. |
| [5] | 白婧, 黄志精, 唐国宁. 用运动控制器来终止心律失常[J]. 计算物理, 2021, 38(3): 352-360. |
| [6] | 黄志精, 白婧, 唐国宁. 单向耦合神经元网络中螺旋波的自发形成机制[J]. 计算物理, 2020, 37(5): 612-622. |
| [7] | 张学良, 谭惠丽, 唐国宁, 邓敏艺. 心肌组织机械形变的元胞自动机模拟[J]. 计算物理, 2018, 35(3): 294-302. |
| [8] | 杨翠云, 刘海英, 唐国宁. 两阶段脉冲控制螺旋波的数值模拟[J]. 计算物理, 2014, 31(5): 625-630. |
| [9] | 陈茜琼, 邓敏艺, 唐国宁, 孔令江. 传导延迟对螺旋波动力学行为的影响[J]. 计算物理, 2013, 30(4): 620-626. |
| [10] | 陈绍英, 袁国勇, 吴刚, 崔倩倩, 范红领. Lévy噪声与周期力共同驱动下的螺旋波动力学[J]. 计算物理, 2012, 29(4): 620-626. |
| [11] | 黎广钊, 唐国宁. 激发介质中去极化对螺旋波动力学影响的数值研究[J]. 计算物理, 2011, 28(4): 626-632. |
| [12] | 钟敏, 唐国宁. 通过控制钙和钾离子流抑制心脏中的螺旋波和时空混沌[J]. 计算物理, 2011, 28(1): 119-124. |
| [13] | 杨先清, 张伟, 仇康, 孙大鹏, 赵跃民. 速度限制对交通流的影响[J]. 计算物理, 2007, 24(4): 499-504. |
| [14] | 马军, 吴宁杰, 应和平, 蒲忠胜. 局部相空间压缩实现对时空混沌和螺旋波的控制[J]. 计算物理, 2006, 23(2): 243-248. |
| [15] | 闫广武. 激励介质中非线性化学波的格子Boltzmann模型[J]. 计算物理, 2003, 20(4): 356-358. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
