随机边界诱导Izhikevich神经元网络的时空模式转换

doi:10.19596/j.cnki.1001-246x.8632

摘要/Abstract

摘要：

在随机边界条件下构建由200 × 200个Izhikevich神经元组成的方形网络, 并利用计算机模拟计算方形网络的时空特性和同步因子, 对神经元的放电模式、分岔现象以及方形网络的时空模式和同步性质进行研究。研究结果表明: 在相同电流刺激和耦合强度下, 由不同放电模式Izhikevich神经元构建的方形网络中, 仅当神经元处于Regular Spiking放电模式下才能在网络中观察到螺旋波种子的出现和消失; 对于其他放电模式(Fast Spiking, Chattering和Intrinsically Bursting)的Izhikevich神经元构建的方形网络, 则无法观察到螺旋波种子的出现。当外界电流刺激恒定时, 只有当神经元之间的耦合强度为中等大小时才可在方形网络中观察到螺旋波种子的出现和消亡, 相对较小或较大的耦合强度不能诱导神经元网络出现螺旋波种子。对方形神经网络中的同步因子研究发现同步因子随耦合强度的变化存在类似"反共振"的形式。

关键词: 螺旋波, 时空, 神经元, 随机, 网络, 模式转换

Abstract:

Izhikevich neuronal model is based on the modeling of cortical and thalamic neurons. This model has the characteristics of being closer to the discharge properties of real biological neurons and it is convenient for large-scale simulation. A square neural network composed of 200 × 200 Izhikevich neurons is constructed under random boundary conditions in this paper, the computer simulation method is used to calculate the spatiotemporal characteristics and synchronization factor of the square network, and the firing patterns and bifurcation phenomena of neurons, as well as the spatiotemporal patterns and synchronization properties of the square network are studied. The results show that in the square neural network constructed by Izhikevich neurons with different discharge modes under the same current stimulation and coupling intensity, the emergence and disappearance of spiral wave seeds can be observed in the neural network only when the neurons are in the Regular Spiking discharge mode. On the other hand, spiral wave seeds cannot be observed in the square neural network constructed by Izhikevich neurons with other discharge modes (e.g. Fast Spiking, Chattering, Internally Bursting). When the external current stimulation is constant, only the medium-sized coupling strength between neurons can induce the emergence and extinction of spiral wave seeds in the square neural network, and smaller or larger coupling strength cannot induce spiral wave seeds in the neural network. In addition, the synchronization factor in square neural networks has been investigated.

Key words: spiral waves, spatiotemporal, neurons, stochastic, networks, mode transformation

王国威, 付燕. 随机边界诱导Izhikevich神经元网络的时空模式转换[J]. 计算物理, 2023, 40(5): 622-632.

Guowei WANG, Yan FU. Stochastic Boundary-induced Spatiotemporal Pattern Transformation in Izhikevich Neuronal Networks[J]. Chinese Journal of Computational Physics, 2023, 40(5): 622-632.

图/表 11

表1 不同放电类型神经元对应的控制参数

Table 1 Control parameters of neurons with different discharge types

Types	a	b	c	d
RS	0.02	0.2	-65	8
FS	0.10	0.2	-65	2
CH	0.02	0.2	-50	2
IB	0.02	0.2	-55	4

图1 神经元耦合连接示意图

Fig.1 Schematic diagram of neuron coupling connection

图2 200×200方形网络连接示意图

Fig.2 Schematic diagram of 200×200 square network

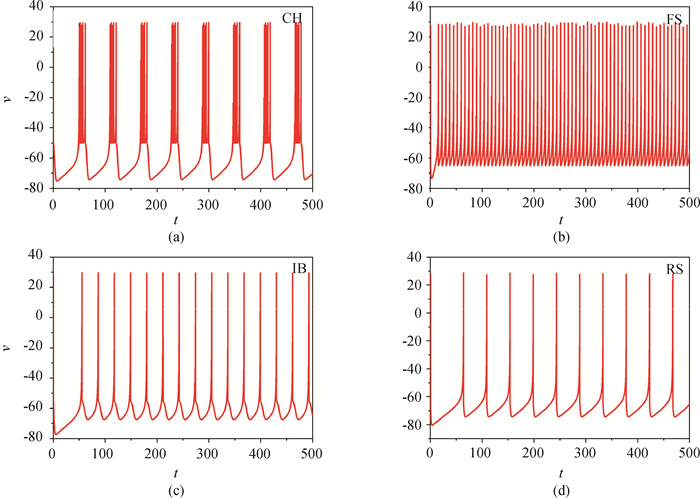
图3 不同类型Izhikevich神经元模型的放电序列图(a) a = 0.02, b = 0.2, c = -50.0, d = 2.0, I = 10;(b) a = 0.1, b = 0.2, c = -65.0, d = 2.0, I = 10; (c) a = 0.02, b = 0.2, c = -55.0, d = 4.0, I =10;(d) a = 0.02, b = 0.2, c = -65.0, d = 8.0, I = 10

Fig.3 Time series diagram of membrane potential of different types of Izhikevich neuron models (a) a = 0.02, b = 0.2, c = -50.0, d = 2.0, I = 10; (b) a = 0.1, b = 0.2, c = -65.0, d = 2.0, I = 10; (c) a = 0.02, b = 0.2, c = -55.0, d = 4.0, I =10; (d) a = 0.02, b = 0.2, c = -65.0, d = 8.0, I = 10

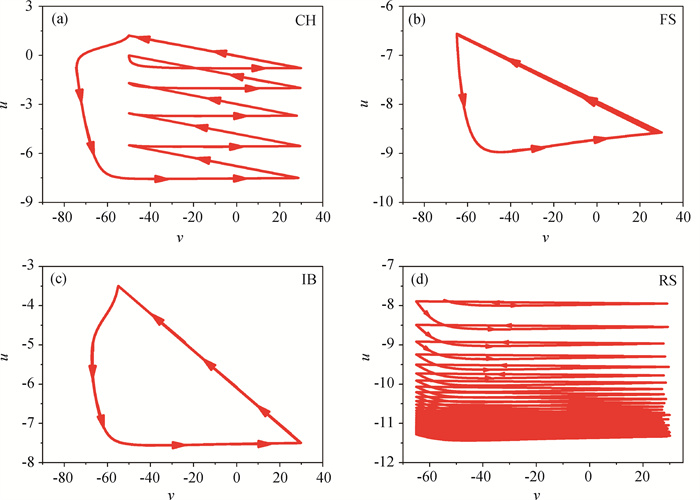
图4 4种不同放电模式的相图(a) a = 0.02, b = 0.2, c = -50.0, d = 2.0, I = 10; (b) a = 0.1, b = 0.2, c = -65.0, d = 2.0, I = 10; (c) a = 0.02, b = 0.2, c = -55.0, d = 4.0, I =10;(d) a = 0.02, b = 0.2, c = -65.0, d = 8.0, I = 10

Fig.4 Phase diagrams of four different discharge modes (a) a = 0.02, b = 0.2, c = -50.0, d = 2.0, I = 10;(b) a = 0.1, b = 0.2, c = -65.0, d = 2.0, I = 10; (c) a = 0.02, b = 0.2, c = -55.0, d = 4.0, I =10;(d) a = 0.02, b = 0.2, c = -65.0, d = 8.0, I = 10

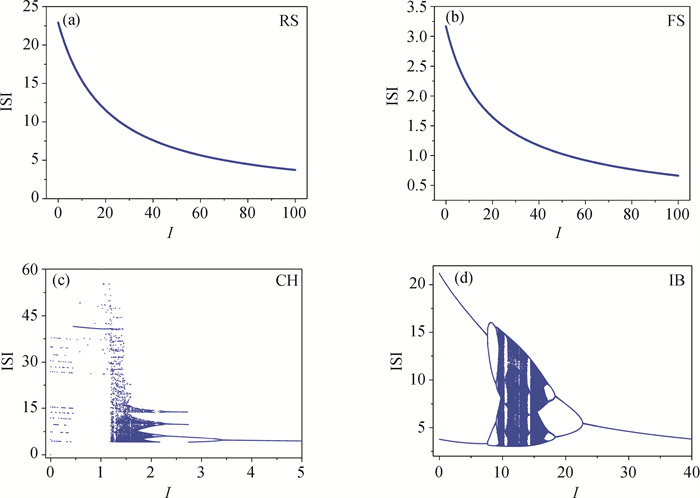
图5 4种不同类型Izhikevich神经元的膜电位随外界刺激电流变化的分叉图(a) a = 0.02, b = 0.2, c = -65.0, d = 8.0; (b) a = 0.1, b = 0.2, c = -65.0, d = 2.0; (c) a = 0.02, b = 0.2, c = -50.0, d = 2.0; (d) a = 0.02, b = 0.2, c = -55.0, d = 4.0

Fig.5 Bifurcation diagram of the membrane potential of four different types of Izhikevich neurons with external stimulation current (a) a = 0.02, b = 0.2, c = -65.0, d = 8.0; (b) a = 0.1, b = 0.2, c = -65.0, d = 2.0;(c) a = 0.02, b = 0.2, c = -50.0, d = 2.0; (d) a = 0.02, b = 0.2, c = -55.0, d = 4.0

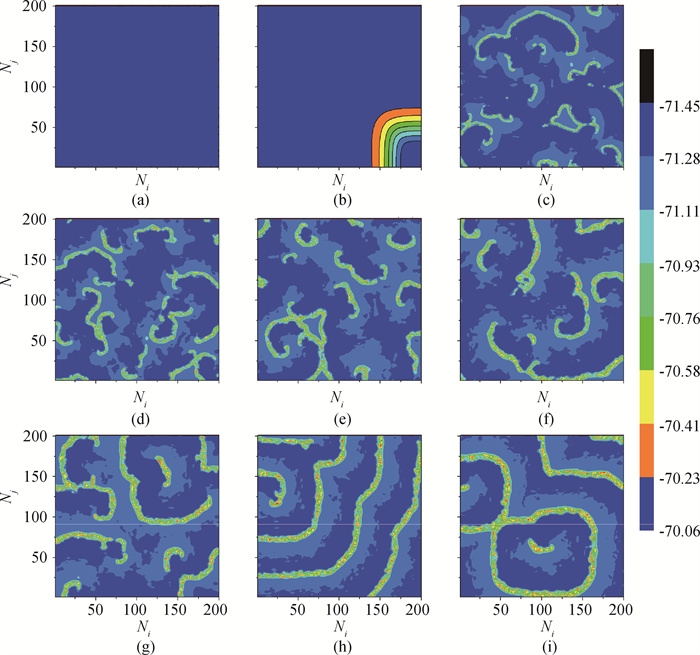
图6 3 000时间单位时改变耦合强度D时随机边界诱导的时空模式转换(a = 0.02, b = 0.2, c = -65.0, d = 8.0, I =10) (a)~(i) D = 0.0, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0

Fig.6 Spatiotemporal pattern transformation induced by random boundary when changing coupling strength D at 3 000 time units (a = 0.02, b = 0.2, c = -65.0, d = 8.0, I = 10) (a)~(i) D = 0.0, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0

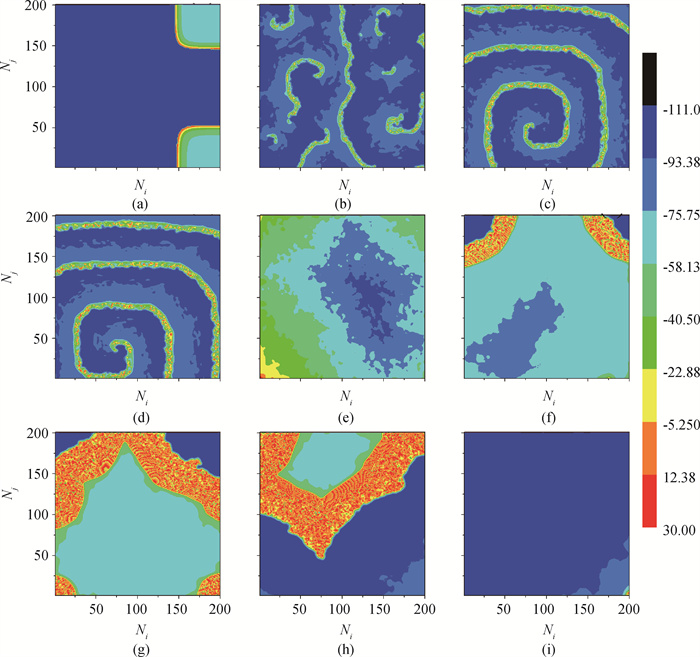
图7 5 000时间单位时改变耦合强度D时随机边界诱导的时空模式转换(a = 0.02, b = 0.2, c = -65.0, d = 8.0, I =10) (a)~(i) D = 0.3, 0.6, 0.9, 1.0, 1.2, 1.5, 1.8, 2.0, 2.1

Fig.7 Spatiotemporal pattern transformation induced by random boundary when changing coupling strength D at 5 000 time unit (a = 0.02, b = 0.2, c = -65.0, d = 8.0, I = 10) (a)~(i) D = 0.3, 0.6, 0.9, 1.0, 1.2, 1.5, 1.8, 2.0, 2.1

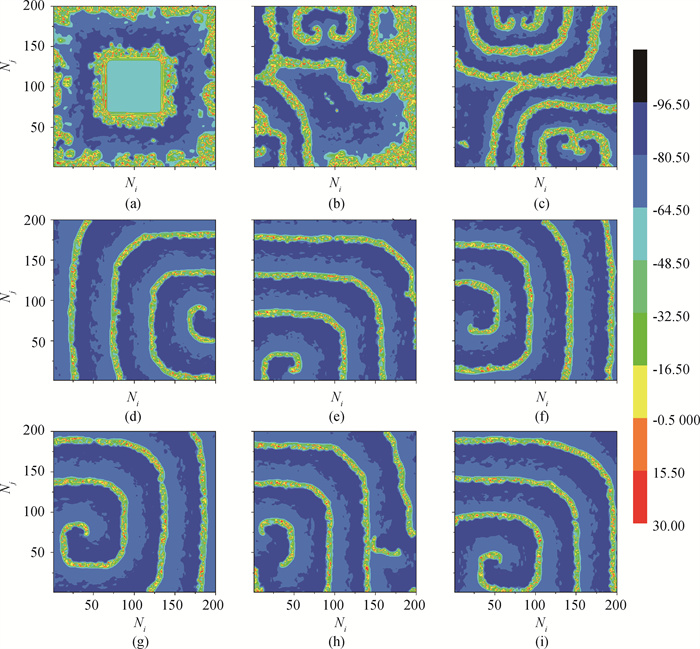
图8 D = 1.0时不同时间单位下随机边界诱导的时空模式转换(a = 0.02, b = 0.2, c = -65.0, d = 8.0, I =10) (a)~(i) t = 50, 500, 1 000, 1 500, 2 000, 2 500, 3 000, 3 500, 4 000

Fig.8 Spatiotemporal pattern transformation induced by random boundary at different time units when D = 1.0 (a = 0.02, b = 0.2, c = -65.0, d = 8.0, I =10) (a)~(i) t = 50, 500, 1 000, 1 500, 2 000, 2 500, 3 000, 3 500, 4 000

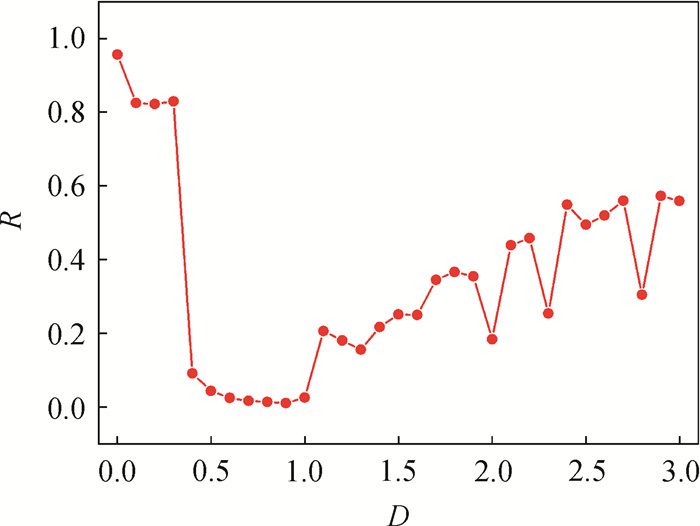
图9 3 000时间单位时方形神经网络对应的同步因子随耦合强度D变化的图像(a = 0.02, b = 0.2, c = -65.0, d = 8.0, I =10)

Fig.9 Synchronization factor corresponding to the square neural network changing with coupling strength D at 3 000 time units (a = 0.02, b = 0.2, c = -65.0, d = 8.0, I =10)

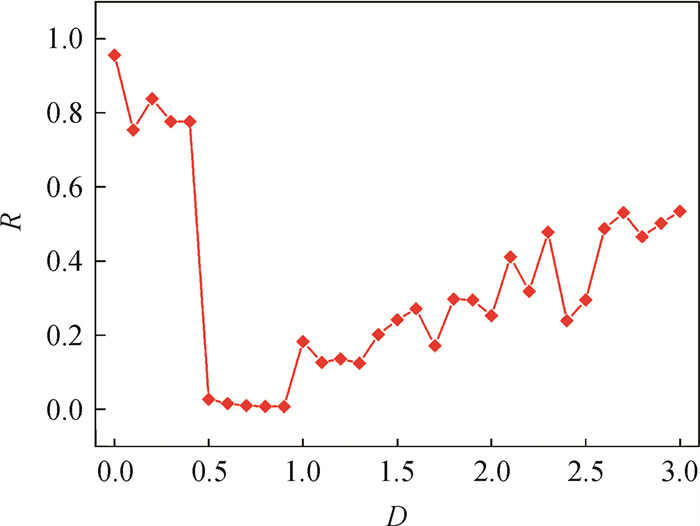
图10 5 000时间单位时方形神经网络对应的同步因子随耦合强度D变化的图像(a = 0.02, b = 0.2, c = -65.0, d = 8.0, I =10)

Fig.10 Synchronization factor corresponding to the square neural network changes with coupling strength D at 5 000 time units (a = 0.02, b = 0.2, c = -65.0, d = 8.0, I =10)

参考文献 47

1	ASE A , CBTA B , AM C , et al. Elimination of spiral waves in a two-dimensional Hindmarsh-Rose neural network under long-range interaction effect and frequency excitation[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 533 (11): 122037.
2	PASHAEI A , BAYER J , MEILLET V , et al. Computation and projection of spiral wave trajectories during atrial fibrillation: A computational study[J]. Cardiac Electrophysiology Clinics, 2015, 7 (1): 37- 47. DOI
3	WANG G W , WU Y , XIAO F L , et al. Non-Gaussian noise and autapse-induced inverse stochastic resonance in bistable Izhikevich neural system under electromagnetic induction[J]. Physica A: Statistical Mechanics and Its Applications, 2022, 598 (7): 127274.
4	WANG G W , GE M Y , LU LL , et al. Study on propagation efficiency and fidelity of subthreshold signal in feed-forward hybrid neural network under electromagnetic radiation[J]. Nonlinear Dynamics, 2021, 103 (3): 2627- 2643. DOI
5	HUANG Z J , BAI J , TANG G N . Mechanism of spontaneous formation of spiral wave in neuronal network with unidirectional coupling[J]. Chinese Journal of Computational Physics, 2020, 37 (5): 612- 622.
6	WANG Z , ROSTAMI Z , JAFARI S , et al. Suppression of spiral wave turbulence by means of periodic plane waves in two-layer excitable media[J]. Chaos, Solitons & Fractals, 2019, 128 (11): 229- 233.
7	张鲁. 变构酶生化反应—扩散体系复杂时空自组织的数值模拟与理论分析[D]. 徐州: 中国矿业大学, 2008.
8	蔡美纯. 可激发系统中螺旋波解析解的研究[D]. 杭州: 浙江大学, 2014.
9	唐冬妮. 非均匀可激发介质中螺旋波动力学行为的研究[D]. 桂林: 广西师范大学, 2010.
10	邝玉兰, 唐国宁. 利用短期心脏记忆消除螺旋波和时空混沌[J]. 物理学报, 2012, 61 (19): 190501.
11	刘海英, 杨翠云, 唐国宁. 心脏老化和收缩对螺旋波动力学的影响研究[J]. 物理学报, 2013, 61 (1): 010505.
12	马军, 谢振博, 陈江星. 热敏神经元网络中螺旋波死亡和破裂的数值模拟[J]. 物理学报, 2012, 61 (3): 038701.
13	王小艳, 汪芃, 李倩昀, 等. 用晚钠电流终止心脏中的螺旋波和时空混沌[J]. 物理学报, 2017, 66 (13): 138201.
14	徐莹, 王春妮, 靳伍银, 等. 梯度耦合下神经元网络中靶波和螺旋波的诱发研究[J]. 物理学报, 2015, 64 (19): 198801. DOI
15	王荣, 吴莹, 刘少宝. 随机中毒对神经元网络时空动力学行为的影响[J]. 物理学报, 2013, 62 (22): 220504. DOI
16	AIHARA , KAZUYUKI , O KU , et al. Elimination of spiral waves in a locally connected chaotic neural network by a dynamic phase space constraint[J]. Neural Networks: The official Journal of the International Neural Network Society, 2017, 88 (4): 9- 21.
17	HUANG X Y , TROY W C , YANG Q , et al. Spiral waves in disinhibited mammalian neocortex[J]. J Neurosci, 2004, 24 (44): 9897- 9902. DOI
18	SCHIFF S J , HUANG X Y , WU J Y . Dynamical evolution of spatiotemporal patterns in mammalian middle cortex[J]. Phys Rev Lett, 2007, 98 (4): 178102.
19	FAURE J , LACHENAL G , COURT M , et al. Exosomes are released by cultured cortical neurones[J]. Molecular & Cellular Neuroscience, 2006, 31 (4): 642- 648.
20	GRAY R A , PERTSOW A M , JALIFE J . Erratum: Spatial and temporal organization during cardiac fibrillation[J]. Nature, 1998, 393 (5): 191- 202.
21	KARMA A . Spiral breakup in model equations of action potential propagation in cardiac tissue[J]. Phys Rev Lett, 1993, 71 (7): 1103- 1106. DOI
22	IZHIKEVICH E M . Simple model of spiking neurons[J]. IEEE Transactions on Neural Networks, 2003, 14 (6): 1569- 1572. DOI
23	WANG G W , YANG L J , ZHAN X , et al. Chaotic resonance in Izhikevich neural network motifs under electromagnetic induction[J]. Nonlinear Dynamics, 2022, 107 (9): 3945- 3962.
24	张伟, 乔清理, 郑旭媛, 等. Izhikevich神经元网络的同步与联想记忆[J]. 生物物理学报, 2008, 24 (4): 298- 302. DOI
25	KAMPAKIA S . Improved Izhikevich neurons for spiking neural networks[J]. Soft Computing, 2012, 16 (6): 943- 953. DOI
26	SOU N , HARUHIKO N , TERUYA Y , et al. Analysis of chaotic resonance in Izhikevich neuron model[J]. Plos One, 2015, 10 (9): e0138919. DOI
27	OLIVEIRA L , GOMES R M , SANOS B A , et al. Effects of the parameters on the oscillation frequency of Izhikevich spiking neural networks[J]. Neurocomputing, 2019, 337 (14): 251- 261.
28	IZHIKEVICH E M . Which model to use for cortical spiking neurons?[J]. IEEE Transactions on Neural Networks, 2004, 15 (5): 1063- 1070. DOI
29	IZHIKEVICH E M . Class 1 neural excitability, conventional synapses, weakly connected networks, and mathematical foundations of pulse-coupled models[J]. IEEE Transactions on Neural Networks, 1999, 10 (3): 499- 507. DOI
30	MA J , LIU Q , YING H , et al. Emergence of spiral wave induced by defects block[J]. Communications in Nonlinear Science & Numerical Simulation, 2013, 18 (7): 1665- 1675.
31	TANG J , LUO J M , MA J , et al. Spiral waves in systems with fractal heterogeneity[J]. Physica A: Statistical Mechanics and Its Applications, 2013, 392 (22): 5764- 5771. DOI
32	WU Y , WANG B , ZHANG X , et al. Spiral wave of a two-layer coupling neuronal network with multi-area channels[J]. International Journal of Modern Physics B, 2019, 33 (29): 1950354. DOI
33	WU X , MA J , FAN L , et al. Development of spiral wave in a regular network of excitatory neurons due to stochastic poisoning of ion channels[J]. Communications in Nonlinear Science & Numerical Simulation, 2013, 18 (12): 3350- 3364.
34	PENG J H , YU H J , LIU Y Z . Associative memory and segmentation in a network composed of spiking neurons[J]. Chinese Journal of Computational Physics, 2005, 22 (4): 337- 343.
35	GE M Y , WANG G W , JIA Y . Influence of the Gaussian colored noise and electromagnetic radiation on the propagation of subthreshold signals in feedforward neural networks[J]. Science China Technological Sciences, 2021, 64 (4): 847- 857. DOI
36	ZHOU Q , WEI D Q . Firing activity of memristive neural network under field coupling[J]. Chinese Journal of Computational Physics, 2020, 37 (6): 750- 756.
37	PAN J , GUO Z L , CHEN S Z . A compound neural network for learning partial differential equations from noisy data[J]. Chinese Journal of Computational Physics, 2022, 39 (2): 223- 232.
38	MENG J , WANG X Y . Robust anti-synchronization of a class of delayed chaotic neural networks[J]. Chinese Journal of Computational Physics, 2008, 25 (2): 247- 252.
39	都琳, 曹子露, 张莹. 感应电场作用下神经元模型的放电机制及稳定性分析[J]. 机械科学与技术, 2017, 36 (2): 202- 206.
40	王国威, 付燕. 关联色噪声对具有免疫监视下肿瘤细胞生长系统稳定性和瞬态性质的影响[J]. 华中师范大学学报(自然科学版), 2021, 55 (1): 36- 45.
41	王国威, 付燕, 彭荣荣. 基于色关联高斯噪声理论下捕食者-被捕食者模型中被捕食者的平均灭绝时间[J]. 华中师范大学学报(自然科学版), 2018, 52 (1): 27- 35.
42	CHENG G X , ZHANG C F . A high-speed neural networks algorithm on classification problem[J]. Chinese Journal of Computational Physics, 1995, 12 (2): 203- 206.
43	TANG L H , HE Z M , YAO Y L . Dynamical analysis and circuit implementation of a memristive Hopfield neural network[J]. Chinese Journal of Computational Physics, 2022, 39 (2): 244- 252.
44	WANG G W , YU D , DING Q M , et al. Effects of electric field on multiple vibrational resonances in Hindmarsh-Rose neuronal systems[J]. Chaos Solitons & Fractals, 2021, 150 (9): 111210- 111210.
45	WANG X Y , TAN G L . Nonlinear prediction and analysis of EEG in a Liley model[J]. Chinese Journal of Computational Physics, 2007, 24 (5): 612- 618.
46	LI T Y , WANG G W , YU D , et al. Synchronization mode transitions induced by chaos in modified Morris-Lecar neural systems with weak coupling[J]. Nonlinear Dynamics, 2022, 108 (3): 2611- 2625.
47	LI H , ZHANG L X , REN Y , et al. Prediction of water temperature of mixed-flow closed cooling tower based on BP neural network and grey correlation analysis[J]. Chinese Journal of Computational Physics, 2022, 39 (1): 53- 59.

[1]	侯凤萍, 邹艳丽, 刘唐慧美, 王志伟, 谭秫毅. 基于区块链的混合式点对点电力信息网络级联故障研究[J]. 计算物理, 2023, 40(5): 633-642.
[2]	李德奎, 毛北行. 时滞干扰环状网络的修正函数投影同步及仿真[J]. 计算物理, 2023, 40(5): 643-652.
[3]	陆丽梅, 韦笃取. 电磁场耦合忆阻Izhikevich神经网络电活动研究[J]. 计算物理, 2023, 40(4): 490-499.
[4]	易智康, 崔国民, 周志强, 肖媛, 熊思恒, 马秀宝. 棋盘模型同步优化质量交换网络[J]. 计算物理, 2023, 40(4): 500-510.
[5]	马秀宝, 崔国民, 周志强, 肖媛, 徐玥, 杨其国. 带有个体淘汰的强制进化随机游走算法优化质量交换网络[J]. 计算物理, 2023, 40(3): 376-388.
[6]	刘丽君, 韦笃取. 忆阻Rulkov神经网络同步研究[J]. 计算物理, 2023, 40(3): 389-400.
[7]	梁炜光, 桑建兵, 田红艳, 段文杰, 陶雅萍, 李烽韬. 基于数据驱动管道流体湍流模型的系数修正及流动特性分析[J]. 计算物理, 2023, 40(1): 57-66.
[8]	孙亮, 罗佳, 乔印虎. 忆阻Hopfield神经网络的初值位移调控动力学及其图像加密应用[J]. 计算物理, 2023, 40(1): 106-116.
[9]	李成乾, 关富荣, 邓敏艺. 传导阻滞和折返效应对螺旋波演化行为的影响[J]. 计算物理, 2023, 40(1): 117-126.
[10]	吴国正, 王发杰, 程隋福, 张成鑫. 基于物理信息神经网络的内部声场正反问题数值计算[J]. 计算物理, 2022, 39(6): 687-698.
[11]	韩新宇, 段欢欢, 崔国民, 肖媛, 杨其国, 张冠华. 公用工程灵活匹配的节点非结构拓展模型[J]. 计算物理, 2022, 39(6): 707-716.
[12]	肖聪, 张士诚, 马新仿, 周彤, 侯腾飞. 基于模型降维和递归神经网络的油藏参数反演[J]. 计算物理, 2022, 39(5): 564-578.
[13]	唐利红, 贺宗梅, 姚延立. 具有隐藏超级多稳定性的磁感应HR神经元及其电路实现[J]. 计算物理, 2022, 39(5): 589-597.
[14]	黄灿, 田冷, 王恒力, 王嘉新, 蒋丽丽. 基于条件生成式对抗网络的油藏单井产量预测模型[J]. 计算物理, 2022, 39(4): 465-478.
[15]	马秀宝, 盖照亮, 崔国民, 周志强, 韩新宇, 杨其国. 基于强制进化随机游走算法的质量交换网络综合[J]. 计算物理, 2022, 39(4): 479-490.