计算物理 ›› 2025, Vol. 42 ›› Issue (1): 10-17.DOI: 10.19596/j.cnki.1001-246x.8810
尹林茂1,2( ), 张玉龙1,3, 杨洋1, 肖福建2, 蒋秉颜3
), 张玉龙1,3, 杨洋1, 肖福建2, 蒋秉颜3
收稿日期:2023-07-31
出版日期:2025-01-25
发布日期:2025-03-08
作者简介:尹林茂, 男, 博士, 讲师, 硕士生导师, 研究方向为CFD程序开发, E-mail: yinlinmao@foxmail.com
基金资助:
Linmao YIN1,2( ), Yulong ZHANG1,3, Yang YANG1, Fujian XIAO2, Bingyan JIANG3
), Yulong ZHANG1,3, Yang YANG1, Fujian XIAO2, Bingyan JIANG3
Received:2023-07-31
Online:2025-01-25
Published:2025-03-08
摘要:
介绍基于速度修正投影技术处理不可压缩Navier-Stokes方程的实施流程, 并引入Picard线性化处理速度控制方程中的对流项, 从而发展出一种基于Picard迭代的速度修正投影法。相较于传统方法, 经过Picard线性化处理后的投影法可以采用更大的时间步长进行求解, 提高了求解方法的稳定性, 并且收敛精度也符合要求, 证实了求解方法的可靠性。
尹林茂, 张玉龙, 杨洋, 肖福建, 蒋秉颜. 一种基于Picard迭代求解不可压缩Navier-Stokes方程的速度修正投影法[J]. 计算物理, 2025, 42(1): 10-17.
Linmao YIN, Yulong ZHANG, Yang YANG, Fujian XIAO, Bingyan JIANG. Velocity-correction Schemes for Solving Incompressible Navier-Stokes Equations Based on Picard Iteration[J]. Chinese Journal of Computational Physics, 2025, 42(1): 10-17.
| 60 | 90 | 120 | 150 | 收敛阶 | |
| E2u-TPM | 4.64×10-4 | 2.01×10-4 | 1.14×10-4 | 7.39×10-5 | 1.952 3 |
| E2u-PPM | 4.16×10-4 | 1.87×10-4 | 1.06×10-4 | 6.88×10-5 | 1.954 6 |
| E2v-TPM | 1.28×10-4 | 5.65×10-5 | 3.19×10-5 | 2.05×10-5 | 1.979 2 |
| E2v-PPM | 1.43×10-4 | 6.33×10-5 | 3.56×10-5 | 2.28×10-5 | 1.997 9 |
| E2p-TPM | 9.19×10-4 | 4.22×10-4 | 2.48×10-4 | 1.66×10-4 | 1.820 5 |
| E2p-PPM | 1.64×10-3 | 7.34×10-4 | 4.18×10-4 | 2.72×10-4 | 1.940 8 |
表1 σ=1 000时两种投影法求解Kovasznay流所得E2和收敛阶
Table 1 Comparison of E2 variation with grid and degree of convergence obtained by two projection methods for Kovasznay flow with σ=1 000
| 60 | 90 | 120 | 150 | 收敛阶 | |
| E2u-TPM | 4.64×10-4 | 2.01×10-4 | 1.14×10-4 | 7.39×10-5 | 1.952 3 |
| E2u-PPM | 4.16×10-4 | 1.87×10-4 | 1.06×10-4 | 6.88×10-5 | 1.954 6 |
| E2v-TPM | 1.28×10-4 | 5.65×10-5 | 3.19×10-5 | 2.05×10-5 | 1.979 2 |
| E2v-PPM | 1.43×10-4 | 6.33×10-5 | 3.56×10-5 | 2.28×10-5 | 1.997 9 |
| E2p-TPM | 9.19×10-4 | 4.22×10-4 | 2.48×10-4 | 1.66×10-4 | 1.820 5 |
| E2p-PPM | 1.64×10-3 | 7.34×10-4 | 4.18×10-4 | 2.72×10-4 | 1.940 8 |
| x方向网格数 | 60 | 90 | 120 | 150 | |
| σmin | 传统投影法 | 38 | 43 | 45 | 46 |
| Picard投影法 | 10 | 12 | 15 | 20 |
表2 不同网格下两种投影法求解Kovasznay流的σmin
Table 2 Two projection methods for solving σmin of Kovasznay flow under different grids
| x方向网格数 | 60 | 90 | 120 | 150 | |
| σmin | 传统投影法 | 38 | 43 | 45 | 46 |
| Picard投影法 | 10 | 12 | 15 | 20 |
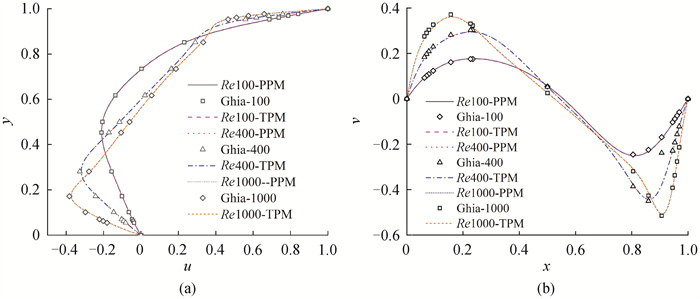
图3 σ=100时,不同Re数下的方腔流中心线上的速度分量(a) x=0.5;(b) y=0.5
Fig.3 Velocity components on the center line of square cavity flow with different Re with σ=100 (a) x=0.5;(b) y=0.5
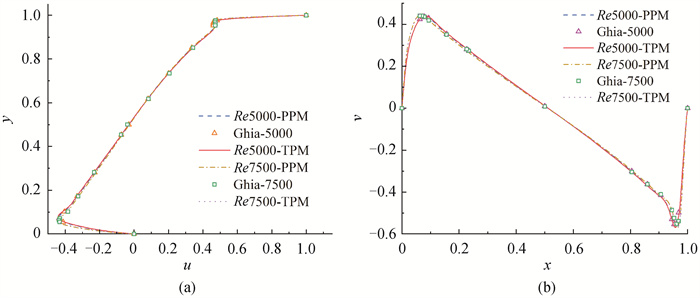
图4 σ=500时, 不同Re数下的方腔流中心线上的速度分量(a) x=0.5;(b) y=0.5
Fig.4 Velocity components on the center line of square cavity flow with different Re with σ=500 (a) x=0.5;(b) y=0.5
| Re | 1 | 100 | 400 | 1 000 | 5 000 | |
| σmin | 传统投影法 | 0.0 | 1.5 | 30.4 | 71.2 | 243.5 |
| Picard投影法 | 0.0 | 0.0 | 5.4 | 23.9 | 147.6 |
表3 不同Re下两种投影法求解方腔顶盖驱动流的σmin
Table 3 Two projection methods for solving σmin of the driven flow of the square cavity top cover under different Re
| Re | 1 | 100 | 400 | 1 000 | 5 000 | |
| σmin | 传统投影法 | 0.0 | 1.5 | 30.4 | 71.2 | 243.5 |
| Picard投影法 | 0.0 | 0.0 | 5.4 | 23.9 | 147.6 |
| Re | 传统投影法 | Picard投影法 | |||
| 最优σ | 迭代步数 | 最优σ | 迭代步数 | ||
| 400 | 30.4 | 1 706 | 5.4 | 525 | |
| 1 000 | 71.2 | 8 131 | 23.9 | 3 037 | |
表4 不同Re下求解方腔顶盖驱动流的最优σ和收敛所需迭代步数
Table 4 Number of iterations required to solve the optimal σ and convergence of flow driven by the square cavity head under different Re
| Re | 传统投影法 | Picard投影法 | |||
| 最优σ | 迭代步数 | 最优σ | 迭代步数 | ||
| 400 | 30.4 | 1 706 | 5.4 | 525 | |
| 1 000 | 71.2 | 8 131 | 23.9 | 3 037 | |
| Ra | σ | 平均努塞尔数Nu | |||
| 传统投影法 | Picard投影法 | Ref.[ | Ref.[ | ||
| 103 | 1 000 | 1.117 4 | 1.117 9 | 1.118 0 | 1.114 0 |
| 104 | 1 000 | 2.245 5 | 2.245 1 | 2.243 0 | 2.245 0 |
| 105 | 5 000 | 4.524 5 | 4.522 9 | 4.451 9 | 4.510 0 |
| 106 | 25 000 | 8.830 4 | 8.827 6 | 8.800 0 | 8.806 0 |
表5 本文和文献平均努塞尔数
Table 5 The average Nusselt number in this paper and the literature
| Ra | σ | 平均努塞尔数Nu | |||
| 传统投影法 | Picard投影法 | Ref.[ | Ref.[ | ||
| 103 | 1 000 | 1.117 4 | 1.117 9 | 1.118 0 | 1.114 0 |
| 104 | 1 000 | 2.245 5 | 2.245 1 | 2.243 0 | 2.245 0 |
| 105 | 5 000 | 4.524 5 | 4.522 9 | 4.451 9 | 4.510 0 |
| 106 | 25 000 | 8.830 4 | 8.827 6 | 8.800 0 | 8.806 0 |
| Ra | 103 | 3×103 | 104 | 105 | 106 | |
| σmin | 传统投影法 | 3 | 50 | 207 | 2 152 | 22 775 |
| Picard投影法 | 0 | 0 | 90 | 1 560 | 11 339 |
表6 不同Ra下两种投影法求解自然对流的σmin
Table 6 σmin of natural convection solved by two projection methods at different Ra
| Ra | 103 | 3×103 | 104 | 105 | 106 | |
| σmin | 传统投影法 | 3 | 50 | 207 | 2 152 | 22 775 |
| Picard投影法 | 0 | 0 | 90 | 1 560 | 11 339 |
| 1 |
DOI |
| 2 |
DOI |
| 3 |
DOI |
| 4 |
DOI |
| 5 |
DOI |
| 6 |
DOI |
| 7 |
|
| 8 |
|
| 9 |
DOI |
| 10 |
DOI |
| 11 |
DOI |
| 12 |
REHMAN M U, VUIK C, SEGAL G. Numerical solution techniques for the steady incompressible Navier-Stokes problem[C]//Proceedings of the World Congress on Engineering 2008 Vol Ⅱ. London: WCE, 2008: 1-6.
|
| 13 |
邱周华, 曾忠, 刘浩. 基于Picard迭代的PN×PN-2谱元法求解定常不可压缩Navier-Stokes方程[J]. 应用数学和力学, 2021, 42 (2): 142- 150.
|
| 14 |
DOI |
| 15 |
秦国良, 徐忠. 谱元方法求解二维不可压缩Navier-Stokes方程[J]. 应用力学学报, 2000, 17 (4): 20- 25.
|
| 16 |
DOI |
| 17 |
DOI |
| 18 |
杨晓成, 尚月强. 大雷诺数Navier-Stokes方程的两水平亚格子模型稳定化方法[J]. 计算物理, 2017, 34 (6): 657- 665.
DOI |
| 19 |
马东军, 柳阳, 孙德军, 等. 高阶谱元区域分解算法求解定常方腔驱动流[J]. 计算力学学报, 2006, 23 (6): 668- 673.
|
| 20 |
丁琪, 尚月强. 非定常Navier-Stokes方程基于两重网格离散的有限元并行算法[J]. 计算物理, 2020, 37 (1): 10- 18.
DOI |
| 21 |
王湛煌, 郑波, 尚月强. 非定常Navier-Stokes方程的并行两水平稳定有限元算法[J]. 计算物理, 2023, 40 (1): 14- 28.
DOI |
| 22 |
DOI |
| 23 |
方季琳, 黄鹏展, 张秋雨. 自然对流问题的一种自适应有限元方法[J]. 厦门大学学报(自然科学版), 2020, 59 (4): 516- 521.
|
| 24 |
DOI |
| 25 |
DOI |
| 26 |
DOI |
| [1] | 王雅莉, 郑波, 尚月强. 定常不可压Navier-Stokes方程的两水平grad-div稳定化有限元方法[J]. 计算物理, 2024, 41(4): 418-425. |
| [2] | 王国梁, 郑波, 尚月强. 带阻尼项定常Navier-Stokes方程的并行两水平有限元算法[J]. 计算物理, 2023, 40(5): 535-547. |
| [3] | 王湛煌, 郑波, 尚月强. 非定常Navier-Stokes方程的并行两水平稳定有限元算法[J]. 计算物理, 2023, 40(1): 14-28. |
| [4] | 李馨东, 赵英奎, 胡宗民, 姜宗林. 基于第二粘性的Navier-Stokes方程组求解正激波结构[J]. 计算物理, 2020, 37(5): 505-513. |
| [5] | 丁琪, 尚月强. 非定常Navier-Stokes方程基于两重网格离散的有限元并行算法[J]. 计算物理, 2020, 37(1): 10-18. |
| [6] | 杨晓成, 尚月强. 大雷诺数Navier-Stokes方程的两水平亚格子模型稳定化方法[J]. 计算物理, 2017, 34(6): 657-665. |
| [7] | 陈德祥, 徐自力, 刘石, 冯永新. Navier-Stokes方程的最小二乘等几何方法[J]. 计算物理, 2014, 31(3): 285-291. |
| [8] | 罗雨鸥, 宇燕, 罗振东. 抛物化Navier-Stokes方程的降维仿真模型[J]. 计算物理, 2014, 31(1): 11-20. |
| [9] | 卓长飞, 武晓松, 封锋, 谢爱元. 基于格子Boltzmann方法的超声速非平衡流模拟[J]. 计算物理, 2013, 30(5): 659-666. |
| [10] | 尚月强, 何银年. 非定常Navier-Stokes方程基于完全重叠型区域分解的有限元并行算法[J]. 计算物理, 2011, 28(2): 181-187. |
| [11] | 韩忠华, 宋文萍, 乔志德. YLSG 107高升力翼型主动流动控制的数值模拟[J]. 计算物理, 2009, 26(6): 837-841. |
| [12] | 韩忠华, 宋文萍, 乔志德. 一种隐式预处理方法及其在定常和非定常流动数值模拟中的应用[J]. 计算物理, 2009, 26(5): 679-684. |
| [13] | 马岩, 胡健伟. 计算圆柱绕流拉力系数的自适应迎风有限元方法[J]. 计算物理, 2009, 26(3): 378-388. |
| [14] | 邓枫, 伍贻兆, 刘学强. 用DES数值模拟分离绕流中的旋涡运动[J]. 计算物理, 2008, 25(6): 683-688. |
| [15] | 高慧, 周晓君. 一种求解可压缩Navier-Stokes方程的隐式迭代时间推进方法[J]. 计算物理, 2008, 25(1): 51-57. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
