计算物理 ›› 2025, Vol. 42 ›› Issue (1): 18-27.DOI: 10.19596/j.cnki.1001-246x.8820
收稿日期:2023-08-14
出版日期:2025-01-25
发布日期:2025-03-08
通讯作者:
热合买提江·依明
作者简介:张秀霞, 女, 硕士研究生, 研究方向为数值计算及其模拟研究, E-mail: 1540842363@qq.com
基金资助:
Xiuxia ZHANG( ), Imin RAHMATJAN*(
), Imin RAHMATJAN*( )
)
Received:2023-08-14
Online:2025-01-25
Published:2025-03-08
Contact:
Imin RAHMATJAN
摘要:
将光滑粒子流体动力学(SPH)方法基础上提出的避免核函数导数的SPH (KDF-SPH)方法应用到时间分数阶对流扩散方程的数值求解。在时间分数阶对流扩散方程的模拟计算过程中, 对Caputo时间分数阶导数采用有限差分方法(FDM), 对空间导数分别采用KDF-SPH方法和SPH方法。结果表明: KDF-SPH方法比SPH方法误差小。KDF-SPH保留了SPH (无网格、拉格朗日和粒子性质)的优点, 该方法在减少误差以及保持稳定性方面发挥了较大作用。无论核梯度是否存在, 数值近似都可以进行, 避免了核函数导数的计算, 降低了对核函数可导性的要求, 提高了计算效率, 易于编程实现, 便于扩展高维问题的计算。
张秀霞, 热合买提江·依明. KDF-SPH方法在分数阶对流扩散方程数值解中的应用[J]. 计算物理, 2025, 42(1): 18-27.
Xiuxia ZHANG, Imin RAHMATJAN. Application of KDF-SPH Method in Numerical Solution of Fractional Convection-diffusion Equation[J]. Chinese Journal of Computational Physics, 2025, 42(1): 18-27.
| 粒子数 | SPH方法 | KDF-SPH方法 | |||
| L∞ | L2 | L∞ | L2 | ||
| 21 | 0.187 824 245 | 0.029 230 384 9 | 2.826 246 99×10-5 | 4.387 049 88×10-6 | |
| 41 | 0.188 761 281 | 0.021 279 728 1 | 5.966 435 60×10-6 | 6.713 923 22×10-7 | |
| 81 | 0.189 222 271 | 0.015 270 329 2 | 3.915 911 05×10-7 | 3.192 811 04×10-8 | |
| 161 | 0.189 461 295 | 0.010 878 059 2 | 1.004 535 21×10-6 | 5.712 619 91×10-8 | |
表1 一维常系数问题取不同粒子所产生误差范数
Table 1 Error norms generated by different particles in one-dimensional constant coefficient problem
| 粒子数 | SPH方法 | KDF-SPH方法 | |||
| L∞ | L2 | L∞ | L2 | ||
| 21 | 0.187 824 245 | 0.029 230 384 9 | 2.826 246 99×10-5 | 4.387 049 88×10-6 | |
| 41 | 0.188 761 281 | 0.021 279 728 1 | 5.966 435 60×10-6 | 6.713 923 22×10-7 | |
| 81 | 0.189 222 271 | 0.015 270 329 2 | 3.915 911 05×10-7 | 3.192 811 04×10-8 | |
| 161 | 0.189 461 295 | 0.010 878 059 2 | 1.004 535 21×10-6 | 5.712 619 91×10-8 | |
| 粒子数 | SPH方法 | KDF-SPH方法 | |||
| L∞ | L2 | L∞ | L2 | ||
| 21 | 0.426 023 65 | 0.065 691 974 5 | 0.012 750 278 14 | 0.082 466 900 91 | |
| 41 | 0.400 575 14 | 0.044 381 002 9 | 0.054 684 664 84 | 0.006 040 478 08 | |
| 81 | 0.386 139 20 | 0.030 455 404 6 | 0.040 594 508 69 | 0.003 174 262 73 | |
| 161 | 0.381 061 91 | 0.024 589 024 6 | 0.035 873 050 50 | 0.002 288 587 91 | |
表2 一维变系数问题取不同粒子所产生误差范数
Table 2 Error norms generated by different particles in one-dimensional variable coefficient problem
| 粒子数 | SPH方法 | KDF-SPH方法 | |||
| L∞ | L2 | L∞ | L2 | ||
| 21 | 0.426 023 65 | 0.065 691 974 5 | 0.012 750 278 14 | 0.082 466 900 91 | |
| 41 | 0.400 575 14 | 0.044 381 002 9 | 0.054 684 664 84 | 0.006 040 478 08 | |
| 81 | 0.386 139 20 | 0.030 455 404 6 | 0.040 594 508 69 | 0.003 174 262 73 | |
| 161 | 0.381 061 91 | 0.024 589 024 6 | 0.035 873 050 50 | 0.002 288 587 91 | |
| 粒子数 | SPH方法 | KDF-SPH方法 | |||
| L∞ | L2 | L∞/10-5 | L2/10-6 | ||
| 21 | 0.044 363 838 | 0.006 787 726 8 | 5.171 276 14 | 7.655 307 54 | |
| 41 | 0.044 448 379 | 0.004 916 989 0 | 4.715 602 54 | 5.111 371 43 | |
| 81 | 0.044 448 970 | 0.003 519 807 4 | 4.719 726 09 | 3.694 452 17 | |
| 161 | 0.044 451 803 | 0.002 504 346 9 | 4.781 209 45 | 2.675 855 92 | |
表3 一维Burgers问题取不同粒子所产生误差范数
Table 3 Error norms generated by different particles in one-dimensional Burgers problem
| 粒子数 | SPH方法 | KDF-SPH方法 | |||
| L∞ | L2 | L∞/10-5 | L2/10-6 | ||
| 21 | 0.044 363 838 | 0.006 787 726 8 | 5.171 276 14 | 7.655 307 54 | |
| 41 | 0.044 448 379 | 0.004 916 989 0 | 4.715 602 54 | 5.111 371 43 | |
| 81 | 0.044 448 970 | 0.003 519 807 4 | 4.719 726 09 | 3.694 452 17 | |
| 161 | 0.044 451 803 | 0.002 504 346 9 | 4.781 209 45 | 2.675 855 92 | |
| 粒子数 | SPH方法 | KDF-SPH方法 | |||
| L∞ | L2 | L∞ | L2 | ||
| 21 | 1.297 222 0 | 0.202 003 5 | 0.035 649 2 | 0.004 942 0 | |
| 41 | 1.308 954 7 | 0.147 337 7 | 0.035 853 0 | 0.003 586 2 | |
| 81 | 1.313 436 6 | 0.105 832 2 | 0.035 969 3 | 0.002 568 3 | |
| 161 | 1.315 674 7 | 0.075 428 3 | 0.035 981 6 | 0.001 827 5 | |
表4 一维对流边界问题取不同粒子所产生误差范数
Table 4 Error norms generated by different particles in one-dimensional convection boundary problem
| 粒子数 | SPH方法 | KDF-SPH方法 | |||
| L∞ | L2 | L∞ | L2 | ||
| 21 | 1.297 222 0 | 0.202 003 5 | 0.035 649 2 | 0.004 942 0 | |
| 41 | 1.308 954 7 | 0.147 337 7 | 0.035 853 0 | 0.003 586 2 | |
| 81 | 1.313 436 6 | 0.105 832 2 | 0.035 969 3 | 0.002 568 3 | |
| 161 | 1.315 674 7 | 0.075 428 3 | 0.035 981 6 | 0.001 827 5 | |
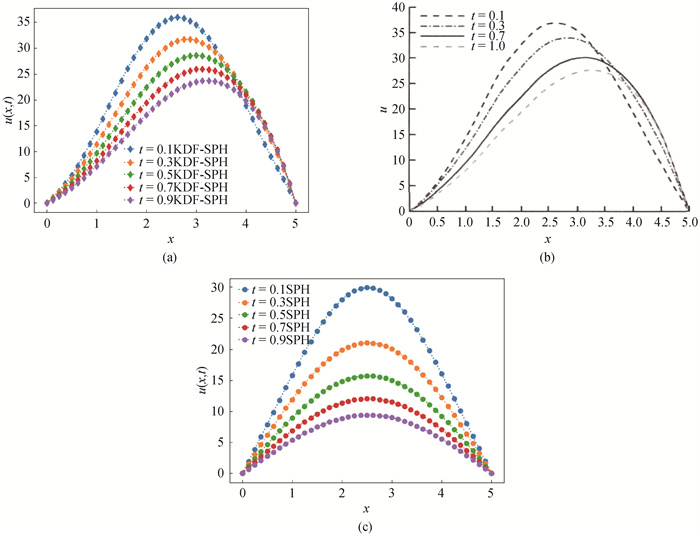
图5 无解析解的问题在不同时刻时浓度扩散图(a) KDF-SPH;(b)Ref.[18];(c) SPH
Fig.5 Concentration diffusion diagram of problem without analytical solution at different time (a) KDF-SPH; (b) Ref. [18]; (c) SPH
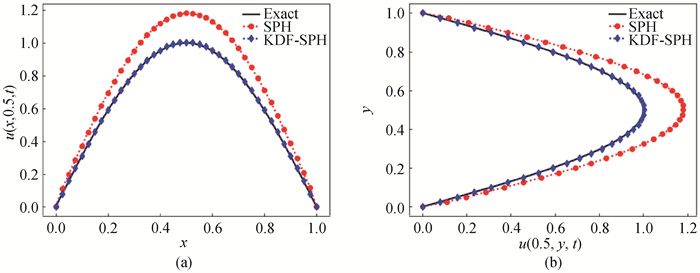
图6 二维问题用不同方法模拟的数值解与精确解(a)y=0.5;(b) x=0.5
Fig.6 Numerical solution and exact solution of two-dimensional problem simulated by different methods (a) y=0.5;(b) x=0.5
| 粒子数 | SPH方法 | KDF-SPH方法 | |||
| L∞ | L2 | L∞ | L2 | ||
| 21 | 0.260 882 9 | 0.053 923 2 | 0.020 470 2 | 0.004 419 4 | |
| 41 | 0.484 058 2 | 0.050 855 9 | 0.024 548 5 | 0.002 318 8 | |
| 81 | 0.935 894 8 | 0.049 633 1 | 0.045 805 4 | 0.001 991 6 | |
| 161 | 1.841 253 9 | 0.049 071 9 | 0.091 089 6 | 0.001 963 8 | |
表5 二维问题取不同粒子所产生的误差范数
Table 5 Error norms generated by different particles in two-dimensional problem
| 粒子数 | SPH方法 | KDF-SPH方法 | |||
| L∞ | L2 | L∞ | L2 | ||
| 21 | 0.260 882 9 | 0.053 923 2 | 0.020 470 2 | 0.004 419 4 | |
| 41 | 0.484 058 2 | 0.050 855 9 | 0.024 548 5 | 0.002 318 8 | |
| 81 | 0.935 894 8 | 0.049 633 1 | 0.045 805 4 | 0.001 991 6 | |
| 161 | 1.841 253 9 | 0.049 071 9 | 0.091 089 6 | 0.001 963 8 | |
| 1 |
吴强, 黄建华. 分数阶微积分[M]. 北京: 清华大学出版社, 2016.
|
| 2 |
|
| 3 |
朱晓钢, 聂玉峰, 王俊刚, 等. 分数阶对流扩散方程的特征有限元方法[J]. 计算物理, 2017, 34 (4): 417- 424.
DOI |
| 4 |
DOI |
| 5 |
DOI |
| 6 |
DOI |
| 7 |
|
| 8 |
DOI |
| 9 |
DOI |
| 10 |
王绍婷. Caputo分数阶导数的高阶逼近方法及其应用[D]. 武汉: 华中科技大学, 2015.
|
| 11 |
DOI |
| 12 |
徐丞君, 徐胜利. SPH二阶粒子近似光滑函数的充分条件及数值验证[J]. 计算物理, 2019, 36 (1): 25- 38.
DOI |
| 13 |
DOI |
| 14 |
|
| 15 |
DOI |
| 16 |
DOI |
| 17 |
彭雪莹. 改进的KGF-SPH方法及其在对流问题中的应用研究[D]. 北京: 北京理工大学, 2023.
|
| 18 |
王星驰. 基于修正SPH方法时/空分数阶对流扩散方程的数值研究[D]. 扬州: 扬州大学, 2021.
|
| 19 |
裴静娴, 热合买提江·依明. 基于有限差分法的SPH边界处理算法及其应用[J]. 计算物理, 2023, 40 (3): 343- 352.
DOI |
| 20 |
|
| 21 |
DOI |
| 22 |
DOI |
| 23 |
DOI |
| 24 |
|
| [1] | 张瑞, 陈雷, 曾文, 鞠迎昕, 李南禹, 宋鹏. 放电电压及介质材料对甲烷介质阻挡放电电离特性的影响[J]. 计算物理, 2025, 42(1): 47-56. |
| [2] | 黄流兴, 卓俊, 李雅琦, 牛胜利, 伏琰军, 李夏至, 朱金辉, 牛进林. 复杂条件下放射性沾染数值模拟研究进展[J]. 计算物理, 2024, 41(6): 797-803. |
| [3] | 淮继茹, 王鹏, 杨梦宇. 液滴碰撞不同接触角线缆表面的模拟[J]. 计算物理, 2024, 41(3): 298-307. |
| [4] | 胡少亮, 徐小文, 安恒斌, 徐然, 范荣红. 应用特征驱动的并行数值代数解法器JPSOL[J]. 计算物理, 2024, 41(1): 110-121. |
| [5] | 王少椿, 付铄然, 郭凌空, 唐志淏, 张娜, 孙乾. 基于模拟有限差分法的水驱油藏渗透率时变数值模拟[J]. 计算物理, 2023, 40(5): 597-605. |
| [6] | 察鲁明, 冯其红, 王森, 徐世乾, 刘高文, 黄文欢. 基于虚拟单元法及损伤模型压驱注水数值模拟方法[J]. 计算物理, 2023, 40(1): 81-90. |
| [7] | 刘利, 牛胜利, 朱金辉, 左应红, 谢红刚, 商鹏. 临近空间核爆炸碎片云运动的数值模拟[J]. 计算物理, 2022, 39(5): 521-528. |
| [8] | 吴丽媛, 张素英. 自旋相关光晶格中玻色-爱因斯坦凝聚体的基态[J]. 计算物理, 2022, 39(5): 617-623. |
| [9] | 杜旭林, 程林松, 牛烺昱, 陈玉明, 曹仁义, 谢永红. 考虑水力压裂缝和天然裂缝动态闭合的三维离散缝网数值模拟[J]. 计算物理, 2022, 39(4): 453-464. |
| [10] | 孙梦营, 马明, 过海龙, 姚孟君, 徐猛, 张莹. 零重力点热源马兰戈尼FTM数值模拟[J]. 计算物理, 2022, 39(2): 191-200. |
| [11] | 赵腾飞, 张华. 气泡碰撞过程中形变及破碎现象分析[J]. 计算物理, 2022, 39(1): 41-52. |
| [12] | 关富荣, 李成乾, 邓敏艺. 激发介质相对不应态对螺旋波动力学行为的影响[J]. 计算物理, 2021, 38(6): 749-756. |
| [13] | 王俊捷, 寇继生, 蔡建超, 潘益鑫, 钟振. 基于Tolman长度的Lucas-Washburn渗吸模型改进及数值模拟[J]. 计算物理, 2021, 38(5): 521-533. |
| [14] | 杨展康, 牛奕. 温度及围护通风对独头巷道氡浓度分布的影响[J]. 计算物理, 2021, 38(4): 456-464. |
| [15] | 胡少亮, 徐小文, 郑宇腾, 赵振国, 王卫杰, 徐然, 安恒斌, 莫则尧. 系统级封装应用中时谐Maxwell方程大规模计算的求解算法:现状与挑战[J]. 计算物理, 2021, 38(2): 131-145. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
