偏心圆环空间内自然对流的确定性及混沌

doi:10.19596/j.cnki.1001-246x.8840

摘要/Abstract

摘要：

使用格子Boltzmann方法(LBM)研究偏心圆环空间内自然对流的非线性特性。通过最大李雅普诺夫指数图谱与游程检验的方法, 数学判定系统在高瑞利数时发展为混沌态; 根据数值解的相空间与功率谱密度(PSD)特性刻画系统通向混沌的历程。结果表明: 随着瑞利数(Ra)的增大, 偏心圆环系统的确定性解经过Hopf分岔转变为周期震荡解, 相空间轨迹由不动点转变为极限环; 随着Ra的进一步增加, 稳定的极限环分岔为二维环面, 系统进入拟周期态; 当Ra达到临界值时, 系统的相空间轨迹呈快速的指数级分离, 变得极其复杂, 其功率谱密度出现大量不可通约的基频, 混沌吸引子出现, Hopf分岔又一次发生, 最终进入混沌。

关键词: 偏心圆环, 自然对流, 格子玻尔兹曼方法, 分岔, 混沌

Abstract:

The nonlinear properties of natural convection in the space of an eccentric annulus are investigated using the lattice Boltzmann method (LBM). Firstly, the system is mathematically determined to develop into a chaotic state at high Rayleigh numbers through the maximum Lyapunov exponent spectrum and run test. Then, the process of the system transitioning to chaos is characterized based on the characteristics of numerical solution phase diagram and power spectral density (PSD). The results show that with the increase of Rayleigh number Ra, the solution of the eccentric annular system changes from deterministic steady-state solution to periodic oscillation solution through Hopf bifurcation, and the phase diagram trajectory changes from fixed point to limit cycle. With further increase of Rayleigh number, the stable limit cycle bifurcates into a two-dimensional torus, and the system enters a quasi-periodic state. When Rayleigh number Ra reaches a critical value, the phase diagram trajectory of the system exhibits rapid exponential separation, becomes extremely complex, and many incommensurable fundamental frequencies appear in its power spectral density. Chaotic attractors emerge, Hopf bifurcation occurs again, and eventually chaos is reached.

Key words: eccentric annulus, natural convection, lattice Boltzmann method, bifurcation, chaos

许一帆, 张虎明, 赵明. 偏心圆环空间内自然对流的确定性及混沌[J]. 计算物理, 2025, 42(1): 28-37.

Yifan XU, Huming ZHANG, Ming ZHAO. Determinism and Chaos of Natural Convection in Eccentric Annulus[J]. Chinese Journal of Computational Physics, 2025, 42(1): 28-37.

图/表 12

图1 几何模型

Fig.1 Physical model

图2 曲边边界示意图

Fig.2 Schematic diagram of curved edges model

图3 等温线的分布(a)文[4]; (b)本文

Fig.3 Distribution of isotherms (a) Ref.[4]; (b) this work

图4 径向无量纲温度分布(Ra=5×104，ε=(0, 180°))

Fig.4 Temperature distributions of radial dimensionless (Ra=5×104, ε=(0, 180°))

图5 不同Ra时系统的最大李雅普诺夫指数图谱( ε =(0, 180°))

Fig.5 The maximum Lyapunov exponent of the system for different Ra ( ε =(0, 180°))

表1 游程检验结果Ra=106，ε= (0, 180°)

Table 1 The results of run test at Ra=106 and ε= (0, 180°)

总个案数	临界值	游程数	Z值	P值
2 001	众数	353	-25.78	0
2 001	中位数	425	-27.80	0
2 001	平均数	356	-25.67	0

图6 监测点状态(a)无量纲温度；(b)u-v相图

Fig.6 State of monitoring point (a) dimensionless temperature; (b))u-v phase diagram

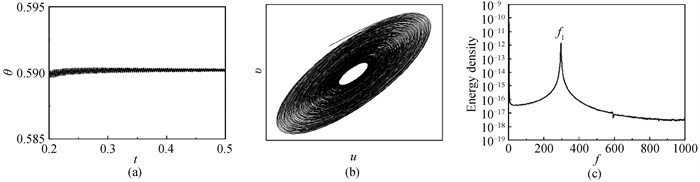
图7 ε =(-0.625, 180°) 时监测点状态(a)无量纲温度；(b))u-v相图；(c)功率谱密度

Fig.7 State of monitoring point at Ra=4×105, ε =(-0.625, 180°) (a) dimensionless temperature; (b))u-v phase diagram; (c) power spectral density

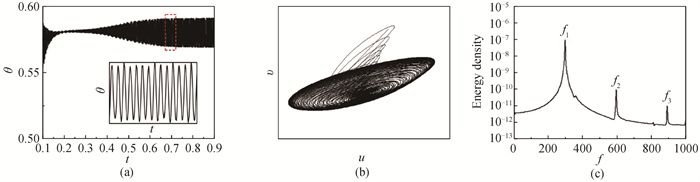
图8 Ra = 5 × 105，ε = (0, 180°) 时监测点状态(a)无量纲温度; (b)u-v相图; (c)功率谱密度

Fig.8 State of monitoring point at Ra = 5 × 105, ε = (0, 180°) (a) dimensionless temperature; (b) u-v phase diagram; (c) power spectral density

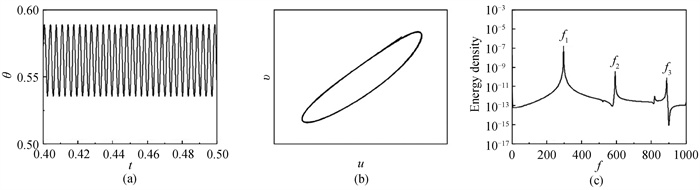
图9 Ra = 7 × 105，ε = (0, 180°) 时监测点状态(a)无量纲温度; (b)u-v相图; (c)功率谱密度

Fig.9 State of monitoring point at Ra = 7 × 105, ε = (0, 180°) (a) dimensionless temperature; (b) u-v phase diagram; (c) power spectral density

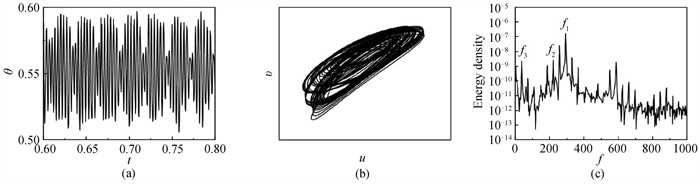
图10 Ra = 8.5 × 105，ε = (0, 180°) 时监测点状态(a)无量纲温度; (b)u-v相图; (c)功率谱密度

Fig.10 State of monitoring point at Ra = 8.5 × 105, ε = (0, 180°) (a) dimensionless temperature; (b) u-v phase diagram; (c) power spectral density

图11 Ra = 106，ε = (0, 180°) 时监测点状态(a)无量纲温度; (b)u-v相图; (c)功率谱密度

Fig.11 State of monitoring point at Ra = 106, ε = (0, 180°) (a) dimensionless temperature; (b) u-v phase diagram; (c) power spectral density

参考文献 22

1	申春赟, 杨茉, 王津, 等. 圆内开缝圆不同开缝方向自然对流换热[J]. 上海理工大学学报, 2013, 35 (5): 425- 429. DOI
2	PETRONE G , CHÉNIER E , LAURIAT G . Three-dimensional study of multiple transitions for natural convection in horizontal annuli[J]. International Journal of Heat and Mass Transfer, 2006, 49 (7/8): 1231- 1241.
3	黄夫泉, 杨茉, 余敏, 等. 封闭圆内开缝圆自然对流换热的振荡特性[J]. 工程热物理学报, 2006, 27 (2): 286- 288. DOI
4	KUEHN T H , GOLDSTEIN R J . An experimental study of natural convection heat transfer in concentric and eccentric horizontal cylindrical annuli[J]. Journal of Heat Transfer, 1978, 100 (4): 635- 640. DOI
5	YOO J S , CHOI J Y , KIM M U . Multicellular natural convection of a low Prandtl number fluid between horizontal concentric cylinders[J]. Numerical Heat Transfer Part A: Applications, 1994, 25 (1): 103- 115. DOI
6	USMAN M , SON J H , PARK I S . A low-Rayleigh transition into chaos for natural convection inside a horizontal annulus at Prandtl number 0.1[J]. International Journal of Heat and Mass Transfer, 2021, 179, 121658. DOI
7	LABONIA G , GUJ G . Natural convection in a horizontal concentric cylindrical annulus: Oscillatory flow and transition to chaos[J]. Journal of Fluid Mechanics, 1998, 375, 179- 202. DOI
8	QIAN Y H . Simulating thermohydrodynamics with lattice BGK models[J]. Journal of Scientific Computing, 1993, 8 (3): 231- 242. DOI
9	CHEN Y , OHASHI H , AKIYAMA M . Two-parameter thermal lattice BGK model with a controllable prandtl number[J]. Journal of Scientific Computing, 1997, 12 (2): 169- 185. DOI
10	CONTRINO D , LALLEMAND P , ASINARI P , et al. Lattice-Boltzmann simulations of the thermally driven 2D square cavity at high rayleigh numbers[J]. Journal of Computational Physics, 2014, 275, 257- 272. DOI
11	GUO Zhaoli , SHI Baochang , ZHENG Chuguang . A coupled lattice BGK model for the Boussinesq equations[J]. International Journal for Numerical Methods in Fluids, 2002, 39 (4): 325- 342. DOI
12	CHAI Zhenhua , YUAN Xiaolei , SHI Baochang . Rectangular multiple-relaxation-time lattice Boltzmann method for the Navier-Stokes and nonlinear convection-diffusion equations: General equilibrium and some important issues[J]. Physical Review E, 2023, 108 (1): 015304. DOI
13	GINZBURG I . Equilibrium-type and link-type lattice Boltzmann models for generic advection and anisotropic-dispersion equation[J]. Advances in Water Resources, 2005, 28 (11): 1171- 1195. DOI
14	CHAI Zhenhua , SHI Baochang , GUO Zhaoli . A multiple-relaxation-time lattice Boltzmann model for general nonlinear anisotropic convection-diffusion equations[J]. Journal of Scientific Computing, 2016, 69 (1): 355- 390. DOI
15	冯舒婷, 戴厚平, 宋通政. 二维空间分数阶反应扩散方程组的格子Boltzmann方法[J]. 计算物理, 2022, 39 (6): 666- 676. DOI
16	HU Yang , LI Decai , SHU Shi , et al. Natural convection in a nanofluid-filled eccentric annulus with constant heat flux wall: A lattice Boltzmann study with immersed boundary method[J]. International Communications in Heat and Mass Transfer, 2017, 86, 262- 273. DOI
17	唐古月, 娄钦, 李凌. 格子Boltzmann方法分析加热尺寸和瑞利数对可变形开口腔内自然对流的影响[J]. 计算物理, 2020, 37 (3): 263- 276. DOI
18	李贝贝, 王婷婷, 陈建, 徐洪涛, 杨茉. 方腔内双扩散混合对流非线性格子Boltzmann研究[J]. 计算物理, 2016, 33 (2): 156- 162. DOI
19	CAO Yuhui , ZHANG Yu . Investigation on the natural convection in horizontal concentric annulus using the variable property-based lattice Boltzmann flux solver[J]. International Journal of Heat and Mass Transfer, 2017, 111, 1260- 1271. DOI
20	LUO Kang , YI Hongliang , TAN Heping . Eccentricity effect on bifurcation and dual solutions in transient natural convection in a horizontal annulus[J]. International Journal of Thermal Sciences, 2015, 89, 283- 293. DOI
21	赵明, 王柯, 余端民. 圆内开缝圆自然对流的Ruelle-Takens混沌道路[J]. 计算物理, 2020, 37 (6): 667- 676. DOI
22	GUO Zhaoli , CHAI Zhenhua , SHI Baochang . An extrapolation method for boundary conditions in lattice Boltzmann method[J]. Physics of Fluids, 2002, 14 (6): 2007- 2010. DOI

[1]	孙书宝, 娄钦. 表征单元体积尺度下多个CaO颗粒吸收CO₂的介观数值方法[J]. 计算物理, 2025, 42(1): 65-76.
[2]	魏如普, 丁鹏. 反演分布函数的多块网格LBM局部加密方法[J]. 计算物理, 2024, 41(5): 643-650.
[3]	王习文, 叶学民, 李丹, 李春曦. 大液滴撞击不同润湿性小球的三维格子Boltzmann方法模拟[J]. 计算物理, 2024, 41(2): 172-181.
[4]	赵双, 陈湘军, 张云贞. 忆阻Lorenz混沌系统的动力学分析与电路实现[J]. 计算物理, 2024, 41(2): 268-276.
[5]	肖彤彤, 李新颖, 钱雨晴. 约瑟夫森结作用下神经元的动力学特性分析[J]. 计算物理, 2023, 40(6): 752-760.
[6]	曹文鑫, 韦笃取. 基于NG-RC电机系统的混沌预测[J]. 计算物理, 2023, 40(4): 519-526.
[7]	孙亮, 罗佳, 乔印虎. 忆阻Hopfield神经网络的初值位移调控动力学及其图像加密应用[J]. 计算物理, 2023, 40(1): 106-116.
[8]	张浏斌, 单彦广, 戎志成. 基于LBM的均匀电场池沸腾单气泡动力学模拟[J]. 计算物理, 2022, 39(5): 537-548.
[9]	刘嘉鑫, 郑林, 张贝豪. 多孔介质方腔内双扩散自然对流熵产的格子Boltzmann模拟[J]. 计算物理, 2022, 39(5): 549-563.
[10]	贾雅琼, 俞斌. 基于重复混沌扩频序列的差分混沌键控系统[J]. 计算物理, 2022, 39(4): 491-497.
[11]	刘凯歌, 韦笃取. 基于WOA-ESN的电机系统混沌振荡预测[J]. 计算物理, 2022, 39(4): 498-504.
[12]	卢英东, 韦笃取. 基于遗传注意力机制的DLSTM电力系统混沌预测[J]. 计算物理, 2022, 39(3): 371-378.
[13]	唐利红, 贺宗梅, 姚延立. 忆阻Hopfield神经网络动力学分析及其电路实现[J]. 计算物理, 2022, 39(2): 244-252.
[14]	徐启程, 孙常春. 具有复合幂函数和共存吸引子的新混沌系统的动力学分析与电路仿真[J]. 计算物理, 2021, 38(6): 742-748.
[15]	郑江韬, 贾宁洪, 胡慧芳, 杨勇, 鞠杨, 王沫然. 分支通道内液-液自发渗吸规律研究[J]. 计算物理, 2021, 38(5): 543-554.