基于深度学习的扩散方程扩散系数反问题求解

doi:10.19596/j.cnki.1001-246x.8892

摘要/Abstract

摘要：

物理信息神经网络(PINN)为偏微分方程正反问题数值求解开创了一条具有广阔应用前景的新途径。本文聚焦于扩散方程的扩散系数反演问题。针对固定系数、各向异性系数、空间依赖系数、时空依赖系数以及非线性扩散系数等问题展开了系统研究, 提出了求解各类问题所需的网络结构及求解方法。数值实验表明, PINN方法在求解扩散系数反问题时只需较少的数据即可反演出较为精确的未知系数, 并在一定噪声水平下表现出较强的稳健性。

关键词: 物理信息神经网络, 微分方程反问题, 扩散方程, 数值解

Abstract:

Physics-Informed Neural Networks (PINN) have provided a new way of numerically solving forward and inverse problems of partial differential equations with promising applications. This paper focuses on the diffusion coefficient inverse problem of the diffusion equation. A systematic study is carried out for the problems of fixed coefficients, anisotropic coefficients, spatial dependence coefficients, spatio-temporal dependence coefficients, and nonlinear diffusion coefficients, and the neural network structure and solution method required for solving each type of problem are proposed. Numerical experiments show that the PINN method can reconstruct the unknown coefficients accurately with less data and is robust under a certain noise level.

Key words: physics-informed neural networks, inverse problem for partial differential equations, diffusion equation, numerical solution

张延庆, 谷同祥. 基于深度学习的扩散方程扩散系数反问题求解[J]. 计算物理, 2025, 42(2): 146-159.

Yanqing ZHANG, Tongxiang GU. Deep Learning Method for Solving Inverse Problem of Diffusion Coefficients for Diffusion Equation[J]. Chinese Journal of Computational Physics, 2025, 42(2): 146-159.

图/表 27

图1 求解常扩散系数反演问题的神经网络结构

Fig.1 Neural network structure for solving inverse problems with constant diffusion coefficients

图2 求解时空依赖扩散系数反演问题的网络结构

Fig.2 Neural network structure for solving inverse problems with spatio-temporal dependent diffusion coefficient

图3 仅空间依赖扩散系数反演的网络结构

Fig.3 Neural network structure for solving inverse problems with space dependent diffusion coefficient

表1 PINN方法反演的扩散系数及相对误差

Table 1 Diffusion coefficients and relative errors by PINN method

结果	噪声水平/%
结果	0	1	5	10
$ \hat{\lambda}$	6.246	6.236	6.374	5.866
$\|\lambda-\hat{\lambda} / \lambda\| $	0.048	0.071	1.994	6.133

图4 t=0.5时刻方程(13)的(a)精确解；(b)PINN方法预测解；(c)逐点误差

Fig.4 (a)Exact solution of Eq.(13) at t=5; (b) Predicted solution by PINN method; (c) Point-wise error

表2 PINN方法预测解的误差

Table 2 Errors in predict solutions by PINN method

误差	噪声水平/%
误差	0	1	5	10
‖e‖₂	0.115 6	0.676 5	2.170	10.20
‖e‖_∞	0.375 0	0.902 6	1.579	6.889

表3 PINN方法反演扩散系数在不同数据点数及噪声水平下的相对误差

Table 3 Relative errors of diffusion coefficients by PINN method in different number of data points and noise levels

数据点数	噪声水平/%
数据点数	0	1	5	10
N=5	0.062	0.192	0.053	1.972
N=10	0.162	0.366	2.954	1.567
N=20	0.058	0.298	0.164	2.026
N=50	0.012	0.242	0.605	0.249
N=100	0.012	0.398	0.281	3.912

表4 PINN方法反演扩散系数Λ1的误差

Table 4 Errors in diffusion coefficients Λ1 by PINN method

误差	噪声水平/%
误差	0	1	5	10
$ \left\|\left(a_{11}-\hat{a}_{11}\right) / a_{11}\right\|$	0.059	0.063	2.833	1.077
$ \left\|\left(a_{22}-\hat{a}_{22}\right) / a_{22}\right\|$	1.094	1.522	22.603	14.105
$ \left\|a_{12}-\hat{a}_{12}\right\|$	0.136 3	7.593	6.216	19.400

图5 (a) 方程(14)的精确解；(b) PINN方法预测解；(c) 逐点误差

Fig.5 (a) Exact solution of Eq.(14); (b) Predicted solution by PINN method; (c) Point-wise error

表5 PINN方法在Λ1参数下方程解的误差

Table 5 Error in predict solutions by PINN method in Λ1

误差	噪声水平/%
误差	0	1	5	10
‖e‖₂	0.036 89	0.214 2	1.842	1.648
‖e‖_∞	0.058 85	0.277 1	1.254	1.221

表6 PINN方法反演扩散系数Λ2的相对误差

Table 6 Relative errors in diffusion coefficients Λ2 by PINN method

误差	噪声水平/%
误差	0	1	5	10
$ \left\|\left(a_{11}-\hat{a}_{11}\right) / a_{11}\right\|$	0.115	0.251	1.022	0.785
$ \left\|\left(a_{22}-\hat{a}_{22}\right) / a_{22}\right\| $	1.564	7.680	25.419	21.586
$ \left\|\left(a_{12}-\hat{a}_{12}\right) / a_{12}\right\|$	0.025	0.204	1.312	13.617

图6 (a) 方程(14)的精确解；(b) PINN方法预测解；(c) 逐点误差

Fig.6 (a) Exact solution of Eq.(14); (b) Predicted solution by PINN method; (c) Point-wise error

表7 PINN方法在Λ2参数下方程解的误差

Table 7 Error in predict solutions by PINN method in Λ2

误差	噪声水平/%
误差	0	1	5	10
‖e‖₂	0.078 35	0.326 6	1.899	2.187
‖e‖_∞	0.112 60	0.304 1	1.102	1.552

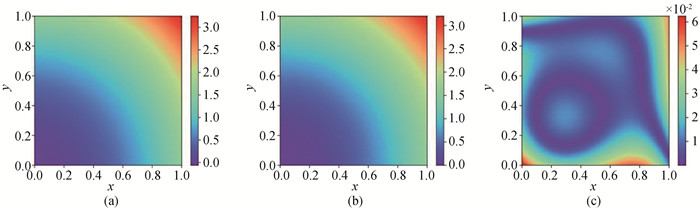
图7 (a) t=0.8时刻扩散系数精确值；(b) PINN方法预测的扩散系数; (c) 逐点误差

Fig.7 (a) Exact values of diffusion coefficients at t=0.8; (b) Diffusion coefficients predicted by PINN method; (c) Point-wise error

表8 PINN方法反演扩散系数a(t, x, y)的误差

Table 8 Errors in the inversion of diffusion coefficients a(t, x, y) by PINN method

误差	噪声水平/%
误差	0	1	5	10
‖e‖₂	1.249	1.245	2.662	41.04
‖e‖_∞	7.189	16.18	22.09	282.7

表9 PINN方法得到预测解的误差

Table 9 Errors in predict solutions by PINN method

误差	噪声水平/%
误差	0	1	5	10
‖e‖₂	0.204 4	0.140 5	0.612 6	4.451
‖e‖_∞	0.658 7	0.289 1	0.915 0	11.81

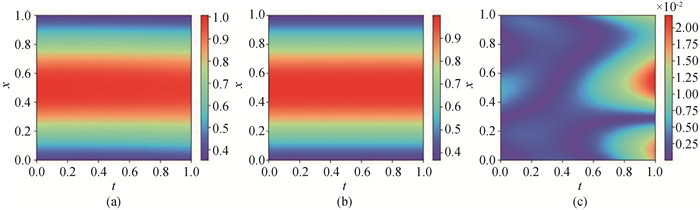
图8 (a) 扩散系数精确值; (b) PINN方法预测的扩散系数; (c) 逐点误差

Fig.8 (a)Exact values of diffusion coefficients; (b) Diffusion coefficients predicted by PINN method; (c) Point-wise error

表10 PINN方法反演扩散系数a(x)的误差

Table 10 Errors in the inversion of diffusion coefficients a(x) by PINN method

误差	噪声水平/%
误差	0	1	5	10
‖e‖₂	0.798	4.049	9.125	32.17
‖e‖_∞	2.188	10.88	22.68	71.21

表11 PINN方法得到方程解的误差

Table 11 Errors in predict solutions by PINN method

误差	噪声水平/%
误差	0	1	5	10
‖e‖₂	0.071 1	0.360 5	1.201	2.733
‖e‖_∞	0.133 5	0.438 8	1.324	3.991

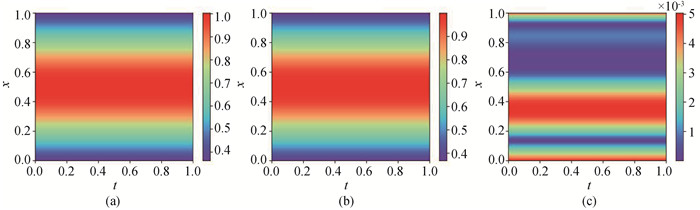
图9 (a) 扩散系数精确值; (b) PINN方法预测的扩散系数; (c) 逐点误差

Fig.9 (a) Exact values of diffusion coefficients; (b) Diffusion coefficients predicted by PINN method; (c) Point-wise error

表12 PINN方法反演扩散系数a(x)的误差

Table 12 Errors in the inversion of diffusion coefficients a(x) by PINN method

误差	噪声水平/%
误差	0	1	5	10
‖e‖₂	0.347 0	0.529 0	1.861	7.185
‖e‖_∞	0.503 6	0.617 5	0.259 5	8.057

表13 PINN方法得到方程解的误差

Table 13 Errors in predict solutions by PINN method

误差	噪声水平/%
误差	0	1	5	10
‖e‖₂	0.110 7	0.199 8	0.497 8	1.638
‖e‖_∞	0.143 0	0.153 7	0.447 4	1.316

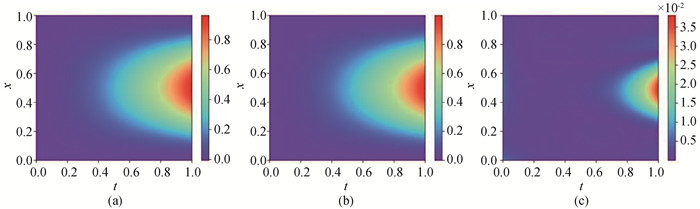
图10 (a) 扩散系数精确值; (b) PINN方法预测的扩散系数; (c) 逐点误差

Fig.10 (a) Exact values of diffusion coefficients; (b) Diffusion coefficients predicted by PINN method; (c) Point-wise error

表14 PINN方法反演扩散系数a(u)的误差

Table 14 Errors in inversion of diffusion coefficients a(u) by PINN method

误差	噪声水平/%
误差	0	1	5	10
‖e‖₂	1.585	2.995	11.65	26.14
‖e‖_∞	3.176	5.971	16.07	38.16

表15 PINN方法得到方程解的误差

Table 15 Errors in predict solutions by PINN method

误差	噪声水平/%
误差	0	1	5	10
‖e‖₂	0.127 5	0.525 2	2.650	3.614
‖e‖_∞	0.189 7	0.814 7	4.539	7.781

表16 PINN方法反演的扩散系数及相对误差

Table 16 Diffusion coefficients and relative errors by PINN method

误差	噪声水平/%
误差	0	1	5	10
$ \|(\mu-\hat{\mu}) / \mu\| $	2.848	7.241	7.902	6.307
$ \|(k-\hat{k}) / k\|$	2.858	1.937	1.018	5.982

表17 PINN方法得到方程解的误差

Table 17 Errors in predict solutions by PINN method

误差	噪声水平/%
误差	0	1	5	10
‖e‖₂	0.078 80	0.225 1	0.466 9	5.636
‖e‖_∞	0.270 4	0.674 8	2.190	2.966

参考文献 31

1	程晋, 刘继军, 张波. 偏微分方程反问题: 模型、算法和应用[J]. 中国科学(数学), 2019, 49 (4): 643- 666.
2	辛志贤, 张启敏, 哈金才. 具有年龄结构的种群扩散系统反问题的数值解[J]. 河南师范大学学报(自然科学版), 2016, 44 (4): 27- 33.
3	ISAKOV V , KINDERMANN S . Identification of the diffusion coefficient in a one-dimensional parabolic equation[J]. Inverse Problems, 2000, 16 (3): 665- 680. DOI
4	GUENTHER R B , SCHMIDT R . Remarks on parameter identification[J]. Numerische Mathematik, 1979, 37 (3): 619- 623.
5	WANG Bingxian , LIU Jijun . Recovery of thermal conductivity in two-dimensional media with nonlinear source by optimizations[J]. Applied Mathematics Letters, 2016, 60, 73- 80. DOI
6	薛齐文, 杨海天, 杜秀云. 同伦正则化算法求解多宗量瞬态热传导反问题[J]. 计算物理, 2006, 23 (2): 151- 157.
7	周焕林, 严俊, 余波, 等. 基于改进布谷鸟算法识别瞬态热传导问题的导热系数[J]. 计算物理, 2018, 35 (2): 212- 220. DOI
8	DUCHATEAU P , THELWELL R , BUTTERS G . Analysis of an adjoint problem approach to the identification of an unknown diffusion coefficient[J]. Inverse Problems, 2004, 20 (2): 601. DOI
9	KEUNG Y L , ZOU J . Numerical identifications of parameters in parabolic systems[J]. Inverse Problems, 1998, 14 (1): 83. DOI
10	BEN-YU G , ZOU J . An augmented lagrangian method for parameter identifications in parabolic systems[J]. Journal of Mathematical Analysis and Applications, 2001, 263 (1): 49- 68. DOI
11	HASANOV A , PEKTAŞ B , ERDEM A . Comparative analysis of inverse coefficient problems for parabolic equations. Part Ⅰ: Adjoint problem approach[J]. Inverse Problems in Science and Engineering, 2011, 19 (5): 599- 615. DOI
12	DENG Zuicha , YANG Liu , YU Jianning , et al. Identifying the diffusion coefficient by optimization from the final observation[J]. Applied Mathematics and Computation, 2013, 219 (9): 4410- 4422. DOI
13	CHANDA S , BALAJI C , VENKATESHAN S P . Non-intrusive measurement of thermal contact conductance at polymer-metal two dimensional annular interface[J]. Heat and Mass Transfer, 2019, 55 (2): 327- 340. DOI
14	HARSHA KUMAR M K , VISHWESHWARA P S , GNANASEKARAN N , et al. A combined ANN-GA and experimental based technique for the estimation of the unknown heat flux for a conjugate heat transfer problem[J]. Heat and Mass Transfer, 2018, 54 (11): 3185- 3197. DOI
15	YANG L , WANG Z . Artificial neural network(ANN)modeling of thermal con-ductivity of supercritical ethane[J]. Energy Sources, Part A: Recovery Utilization and Environmental Effects, 2019, 41 (4): 396- 404. DOI
16	RAISSI M , PERDIKARIS P , KARNIADAKIS G E . Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378, 686- 707. DOI
17	YANG Liu , MENG Xuhui , KARNIADAKIS G E . B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data[J]. Journal of Computational Physics, 2021, 425, 109913. DOI
18	YUAN Lei , NI Yiqing , DENG Xiangyun , et al. A-PINN: auxiliary physics informed neural networks for forward and inverse problems of nonlinear integro-differential equations[J]. Journal of Computational Physics, 2022, 462, 111260. DOI
19	吴国正, 王发杰, 程隋福, 等. 基于物理信息神经网络的内部声场正反问题数值计算[J]. 计算物理, 2022, 39 (6): 687- 698. DOI
20	ZHANG Mengmeng , LI Qianxiao , LIU Jijun . On stability and regularization for data-driven solution of parabolic inverse source problems[J]. Journal of Computational Physics, 2023, 474, 111769.
21	HE Zhili , NI Futao , WANG Weiguo , et al. A physics-informed deep learning method for solving direct and inverse heat conduction problems of materials[J]. Materials Today Communications, 2021, 28, 102719.
22	CAI S , WANG Z , WANG S , et al. Physics-informed neural networks for heat transfer problems[J]. Journal of Heat Transfer, 2021, 143 (6): 060801.
23	张国安. 一类二维多层对流扩散方程参数反演的神经网络方法研究[D]. 上海: 上海财经大学, 2022.
24	李治平. 偏微分方程数值解讲义[M]. 北京: 北京大学出版社, 2010: 32- 36.
25	KINGMA D P, BA J. Adam: a method for stochastic optimization[DB/OL]. arXiv(2017-01-30). https://arxiv.org/abs/1412.6980.
26	NOCEDAL J , WRIGHT S J . Numerical optimization[M]. New York: Springer, 1999.
27	HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA: IEEE, 2016: 770-778.
28	GLOROT X, BENGIO Y. Understanding the difficulty of training deep feedforward neural networks[C]//Proceedings of the thirteenth international conference on artificial intelligence and statistics. Chia Laguna Resort, Sardinia, Italy: PMLR, 2010: 249-256.
29	HENDRYCKS D, GIMPEL K. Gaussian error linear units(gelus)[DB/OL]. arXiv(2023-06-06). http://export.arxiv.org/abs/1606.08415v5.
30	XIE H, ZHAI C, LIU L, et al. A weighted first-order formulation for solving anisotropic diffusion equations with deep neural networks[DB/OL]. arXiv(2022-04-29). https://arxiv.org/abs/2205.06658.
31	TARTAKOVSKY A M , MARRERO C O , PERDIKARIS P , et al. Physics-informed deep neural networks for learning parameters and constitutive relationships in subsurface flow problems[J]. Water Resources Research, 2020, 56 (5): e2019WR026731.

[1]	舒适, 岳孝强, 何剑萌, 徐小文, 莫则尧. 多群辐射扩散问题特征驱动的并行AMG法[J]. 计算物理, 2024, 41(1): 87-97.
[2]	冯舒婷, 戴厚平, 宋通政. 二维空间分数阶反应扩散方程组的格子Boltzmann方法[J]. 计算物理, 2022, 39(6): 666-676.
[3]	吴国正, 王发杰, 程隋福, 张成鑫. 基于物理信息神经网络的内部声场正反问题数值计算[J]. 计算物理, 2022, 39(6): 687-698.
[4]	胡晓燕, 范征锋. 惯性约束聚变内爆中基于多块结构网格的高效辐射扩散并行算法[J]. 计算物理, 2022, 39(3): 277-285.
[5]	张淑娴, 杭旭登. 二维扩散方程的局部二阶线性保极值节点计算方法及应用[J]. 计算物理, 2022, 39(1): 17-32.
[6]	魏雪丹, 戴厚平, 李梦军, 郑洲顺. 一维空间Riesz分数阶对流扩散方程的格子Boltzmann方法[J]. 计算物理, 2021, 38(6): 683-692.
[7]	张佳, 程时清, 曾杨, 张满, 于海洋. 聚合物驱试井分析叠加原理适用性的探索[J]. 计算物理, 2021, 38(3): 324-332.
[8]	徐金景, 袁光伟. 多流管网格上九点格式的节点插值方法[J]. 计算物理, 2021, 38(2): 153-164.
[9]	赵菲, 盛志强, 袁光伟. 基于二阶格式的有限体积保正格式[J]. 计算物理, 2020, 37(4): 379-392.
[10]	朱晓钢, 聂玉峰, 王俊刚, 袁占斌. 分数阶对流扩散方程的特征有限元方法[J]. 计算物理, 2017, 34(4): 417-424.
[11]	郭少冬, 章明宇, 周海兵, 熊俊, 张树道. 三维非匹配网格上的扩散方程数值求解[J]. 计算物理, 2017, 34(1): 19-28.
[12]	吕桂霞, 孙顺凯. 扩散方程的有限方向差分方法[J]. 计算物理, 2015, 32(6): 649-661.
[13]	舒适, 岳孝强, 周志阳, 徐小文. SAMR网格上扩散方程有限体格式的逼近性与两层网格算法[J]. 计算物理, 2014, 31(4): 390-402.
[14]	邓志红, 孙玉良, 李富, Rizwan-uddin. 改进的节块展开方法求解圆柱几何对流扩散方程[J]. 计算物理, 2013, 30(4): 475-482.
[15]	曾凡海, 李常品. 时间分数阶亚扩散方程的高阶差分方法[J]. 计算物理, 2013, 30(4): 491-500.