计算物理 ›› 2024, Vol. 41 ›› Issue (4): 403-417.DOI: 10.19596/j.cnki.1001-246x.8737
毛润彰1,2( ), 杜皓3, 田鸿运2, 黄思路2, 张鹏2,4, 徐小文2,4,*(
), 杜皓3, 田鸿运2, 黄思路2, 张鹏2,4, 徐小文2,4,*( )
)
收稿日期:2023-03-23
出版日期:2024-07-25
发布日期:2024-08-24
通讯作者:
徐小文
作者简介:毛润彰,男,硕士研究生,研究方向为大规模并行计算, E-mail:maorunzhang20@gscaep.ac.cn
基金资助:
Runzhang MAO1,2( ), Hao DU3, Hongyun TIAN2, Silu HUANG2, Peng ZHANG2,4, Xiaowen XU2,4,*(
), Hao DU3, Hongyun TIAN2, Silu HUANG2, Peng ZHANG2,4, Xiaowen XU2,4,*( )
)
Received:2023-03-23
Online:2024-07-25
Published:2024-08-24
Contact:
Xiaowen XU
摘要:
对于大规模稀疏线性代数方程组,代数多重网格(AMG)是具有最优计算复杂度的求解算法,但由于其算法流程复杂,导致难以取得理想的并行可扩展性能,难以定位和分析其并行可扩展瓶颈。通过分析AMG算法的性能骨架和通信模式,归纳了三类可扩展性能瓶颈,并引入稀疏矩阵通信域的概念来刻画稀疏模式对并行通信性能的影响。针对辐射流体力学、结构力学、航空发动机三类实际应用的6个具有不同稀疏模式特征的典型算例,实现了多粒度并行可扩展性能瓶颈的定位与分析,总结了未来AMG并行性能优化方向。
中图分类号:
毛润彰, 杜皓, 田鸿运, 黄思路, 张鹏, 徐小文. 几类典型应用的代数多重网格算法并行可扩展瓶颈分析[J]. 计算物理, 2024, 41(4): 403-417.
Runzhang MAO, Hao DU, Hongyun TIAN, Silu HUANG, Peng ZHANG, Xiaowen XU. Analysis of Parallel Scalability Bottleneck for Algebraic Multigrid in Typical Real Applications[J]. Chinese Journal of Computational Physics, 2024, 41(4): 403-417.
| 算法步骤 | 组件模块 | 内涵 | 计算模式① | 通信模式 |
| 1.1 | Coarsen | 选择粗变量集合 | 图遍历 | 聚合通信,点对点通信 |
| 1.2 | BuildInterp | 构造插值算子 | 图遍历 | 点对点通信 |
| 1.3 | RAP | 三个矩阵相乘 | SpGeMM② | 聚合通信、点对点通信 |
| 2.1 | Smooth | 前光滑、后光滑 | SpTrSV③ | 点对点通信 |
| 2.2 | Restrict | 残差限制 | SpMV④、SpMTV⑤ | 点对点通信 |
| 2.3 | CoarsestSolver | 最粗层求解器 | LU分解 | 点对点通信 |
| 2.4 | Prolong | 插值校正 | SpMV | 点对点通信 |
| 2.6 | ResidualNorm | 计算残差 | SpMV、内积 | 聚合通信、点对点通信 |
表1 AMG算法步骤中涉及的组件模块、内涵、计算模式和通信模式
Table 1 Component modules, implications, computational patterns, and communication patterns involved in the AMG algorithm
| 算法步骤 | 组件模块 | 内涵 | 计算模式① | 通信模式 |
| 1.1 | Coarsen | 选择粗变量集合 | 图遍历 | 聚合通信,点对点通信 |
| 1.2 | BuildInterp | 构造插值算子 | 图遍历 | 点对点通信 |
| 1.3 | RAP | 三个矩阵相乘 | SpGeMM② | 聚合通信、点对点通信 |
| 2.1 | Smooth | 前光滑、后光滑 | SpTrSV③ | 点对点通信 |
| 2.2 | Restrict | 残差限制 | SpMV④、SpMTV⑤ | 点对点通信 |
| 2.3 | CoarsestSolver | 最粗层求解器 | LU分解 | 点对点通信 |
| 2.4 | Prolong | 插值校正 | SpMV | 点对点通信 |
| 2.6 | ResidualNorm | 计算残差 | SpMV、内积 | 聚合通信、点对点通信 |
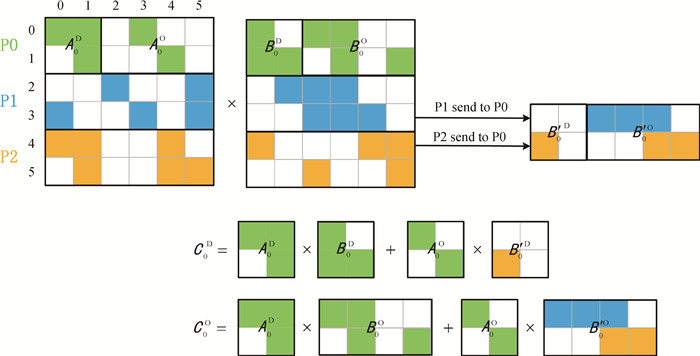
图1 稀疏矩阵乘稀疏矩阵C=AB中点对点通信模式示意图(以0号进程为例展示了具体实现过程,稀疏矩阵A和B按行划分给每个进程,绿色、蓝色和橙色分别代表 0号、1号和2号进程所拥有的矩阵元素。)
Fig.1 Schematic diagram of point-to-point communication mode for sparse matrix multiplication C=AB (The specific implementation process is demonstrated using process 0 as an example. The sparse matrix A and B is partitioned by rows and assigned to each process. Green, blue, and orange represent the matrix elements owned by processes 0, 1, and 2, respectively.)
| 算例名 | 应用领域 | 偏微分方程 | 网格类型 | 离散方法 |
| RHD-1T | 辐射流体力学流体不稳定性 | 三维辐射扩散方程 | 结构网格 | 有限体积7点格式 |
| RHD-3T | 辐射流体力学流体不稳定性 | 三维三温能量方程 | 结构网格 | 有限体积7点格式 |
| SM-LXJ | 离心机装置结构力学分析 | 三维线弹性方程 | 非结构网格 | 有限元 |
| SM-C | 接触问题结构力学分析 | 三维线弹性方程 | 非结构网格 | 有限元 |
| HF-S | 航空发动机整机静力学分析 | 三维线弹性方程 | 非结构网格 | 有限元 |
| HF-C | 航空发动机燃烧室仿真 | 三维压力方程 | 非结构网格 | 有限元 |
表2 测试算例的应用背景
Table 2 Application background of test examples
| 算例名 | 应用领域 | 偏微分方程 | 网格类型 | 离散方法 |
| RHD-1T | 辐射流体力学流体不稳定性 | 三维辐射扩散方程 | 结构网格 | 有限体积7点格式 |
| RHD-3T | 辐射流体力学流体不稳定性 | 三维三温能量方程 | 结构网格 | 有限体积7点格式 |
| SM-LXJ | 离心机装置结构力学分析 | 三维线弹性方程 | 非结构网格 | 有限元 |
| SM-C | 接触问题结构力学分析 | 三维线弹性方程 | 非结构网格 | 有限元 |
| HF-S | 航空发动机整机静力学分析 | 三维线弹性方程 | 非结构网格 | 有限元 |
| HF-C | 航空发动机燃烧室仿真 | 三维压力方程 | 非结构网格 | 有限元 |
| 算例名 | 阶数 | 非零元数 | 平均每行非零元数 | 稠密度 | 带宽 |
| RHD-1T | 2 097 152 | 14 581 760 | 6.95 | 3.32×10-6 | 16 384 |
| RHD-3T | 6 291 456 | 52 133 888 | 8.29 | 1.32×10-6 | 49 152 |
| SM-LXJ | 83 073 | 2 826 927 | 34.03 | 4.10×10-4 | 45 426 |
| SM-C | 12 075 090 | 655 371 242 | 54.27 | 4.49×10-6 | 12 075 079 |
| HF-S | 2 081 541 | 71 033 481 | 34.13 | 1.63×10-5 | 733 683 |
| HF-C | 19 637 808 | 97 535 370 | 4.97 | 2.53×10-7 | 18 234 897 |
表3 测试算例的基本代数特征
Table 3 Basic algebraic characteristics of test examples
| 算例名 | 阶数 | 非零元数 | 平均每行非零元数 | 稠密度 | 带宽 |
| RHD-1T | 2 097 152 | 14 581 760 | 6.95 | 3.32×10-6 | 16 384 |
| RHD-3T | 6 291 456 | 52 133 888 | 8.29 | 1.32×10-6 | 49 152 |
| SM-LXJ | 83 073 | 2 826 927 | 34.03 | 4.10×10-4 | 45 426 |
| SM-C | 12 075 090 | 655 371 242 | 54.27 | 4.49×10-6 | 12 075 079 |
| HF-S | 2 081 541 | 71 033 481 | 34.13 | 1.63×10-5 | 733 683 |
| HF-C | 19 637 808 | 97 535 370 | 4.97 | 2.53×10-7 | 18 234 897 |
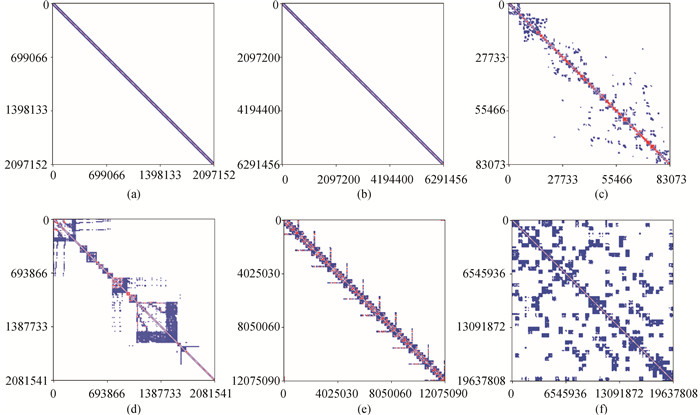
图4 测试算例的矩阵稀疏分布图(a)RHD-1T;(b)RHD-3T;(c)SM-LXJ;(d)SM-C; (e)HF-S;(f)HF-C
Fig.4 Matric sparse distribution of test examples (a)RHD-1T; (b)RHD-3T; (c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C
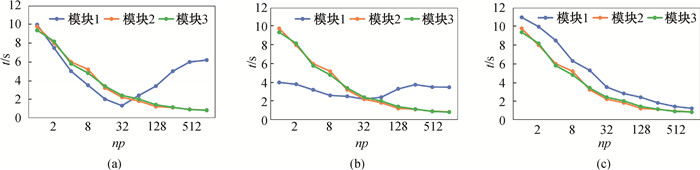
图5 AMG的三类可扩展性能瓶颈(a)第一类;(b)第二类;(c)第三类
Fig.5 Three types of AMG scalable performance bottlenecks (a) the first type; (b) the second type and (c) the third type
| 网格层 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| RHD-1T | 17.0 | 48.3 | 119.2 | 220.7 | 309.1 | 142.4 | 42.4 | |
| RHD-3T | 17.0 | 48.5 | 120.6 | 223.1 | 333.3 | 174.9 | 50.4 | |
| SM-LXJ | 160.2 | 274.2 | 275.3 | 196.3 | 98.3 | 38.1 | 12.2 | |
| SM-C | 127.4 | 103.9 | 107.5 | 150.6 | 180.3 | 25.7 | ||
| HF-S | 189.8 | 244.1 | 273.1 | 272.5 | 229.9 | 128.4 | 38.3 | 12.5 |
| HF-C | 848.9 | 853.0 | 860.5 | 865.4 | 840.9 | 599.0 | 200.7 | 32.6 |
表4 各算例各网格层平均矩阵通信域(L0是最细层网格,进程数为2 048。)
Table 4 Average matrix communication domain of examples at each grid layer (L0 represents the finest grid layer with 2 048 processes.)
| 网格层 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| RHD-1T | 17.0 | 48.3 | 119.2 | 220.7 | 309.1 | 142.4 | 42.4 | |
| RHD-3T | 17.0 | 48.5 | 120.6 | 223.1 | 333.3 | 174.9 | 50.4 | |
| SM-LXJ | 160.2 | 274.2 | 275.3 | 196.3 | 98.3 | 38.1 | 12.2 | |
| SM-C | 127.4 | 103.9 | 107.5 | 150.6 | 180.3 | 25.7 | ||
| HF-S | 189.8 | 244.1 | 273.1 | 272.5 | 229.9 | 128.4 | 38.3 | 12.5 |
| HF-C | 848.9 | 853.0 | 860.5 | 865.4 | 840.9 | 599.0 | 200.7 | 32.6 |
| 插值类型 | 粗化类型 | 光滑类型 | 强连通阈值 | 最粗层矩阵规模阈值 |
| 修正的经典插值[ | HMIS[ | 混合对称的Gauss-Seidel[ | 0.25 | 100 |
表5 AMG解法器测试参数
Table 5 Test parameters of AMG solver
| 插值类型 | 粗化类型 | 光滑类型 | 强连通阈值 | 最粗层矩阵规模阈值 |
| 修正的经典插值[ | HMIS[ | 混合对称的Gauss-Seidel[ | 0.25 | 100 |
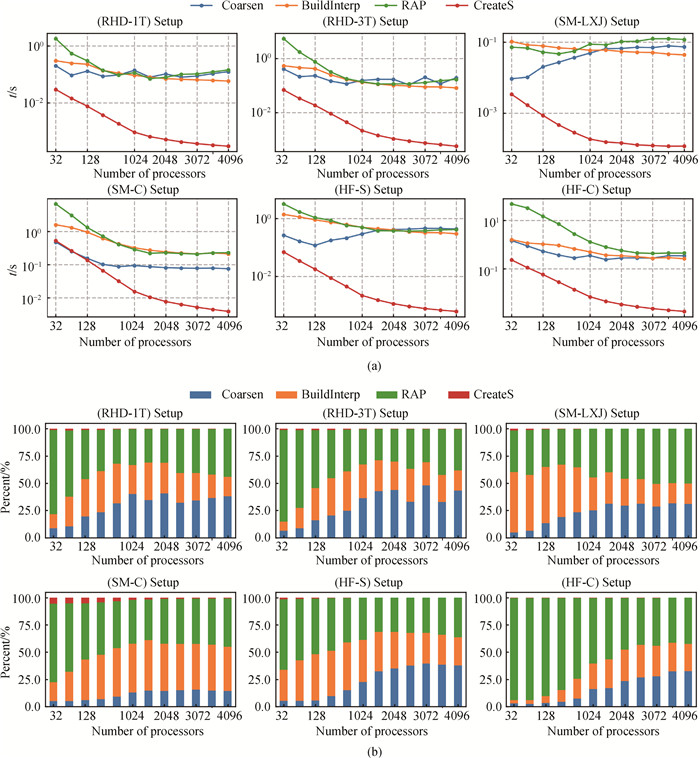
图7 各算例Setup阶段第1级4个组件的时间开销(a)时间占比;(b)随进程数变化趋势图
Fig.7 Time trend chart of four components at Level 1 of the Setup phase (a) time percentage and (b) number of processors

图8 Coarsen组件的FIS模块中4个通信函数的时间开销随进程数变化趋势图 (a)RHD-1T;(b)RHD-3T;(c)SM-LXJ;(d)SM-C; (e)HF-S;(f)HF-C
Fig.8 Time trend chart of 4 communication functions in the FIS module of Coarsen component with number of processes (a)RHD-1T; (b)RHD-3T; (c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C
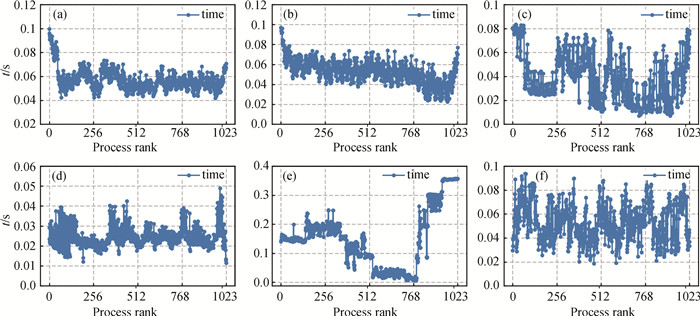
图9 1 024个进程下,每个进程的Allreduce时间开销(a)RHD-1T;(b)RHD-3T;(c)SM-LXJ;(d)SM-C; (e)HF-S;(f)HF-C
Fig.9 Allreduce time per process under 1 024 processes (a)RHD-1T; (b)RHD-3T;(c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C
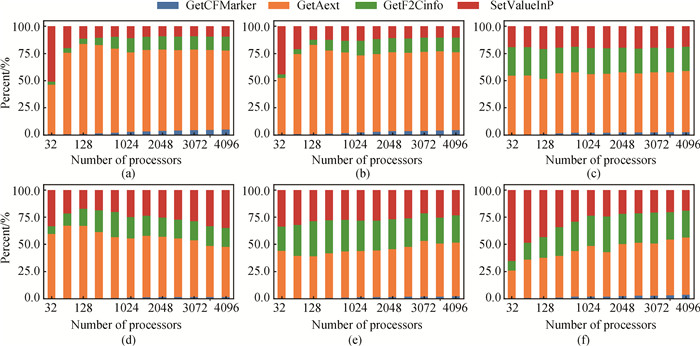
图10 BuidlInterp组件中4个模块的时间百分比随进程数变化趋势图 (a)RHD-1T;(b)RHD-3T;(c)SM-LXJ;(d)SM-C; (e)HF-S;(f)HF-C
Fig.10 The percentage of time of the four modules in the BuildInterp component with number of processes (a)RHD-1T; (b)RHD-3T; (c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C
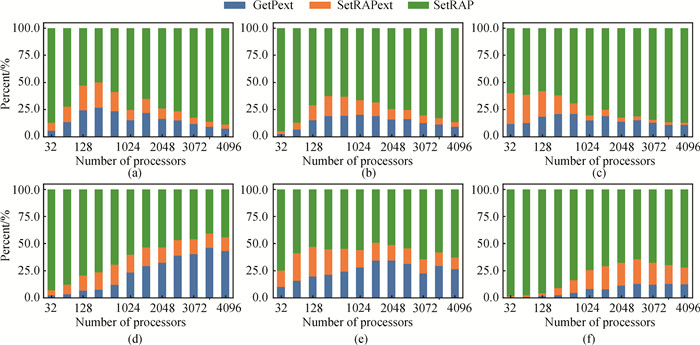
图11 RAP组件中3个模块时间占比随进程数变化趋势图 (a)RHD-1T;(b)RHD-3T;(c)SM-LXJ;(d)SM-C; (e)HF-S;(f)HF-C
Fig.11 The percentage of time of the three modules in the RAP component with number of processes (a)RHD-1T; (b)RHD-3T; (c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C
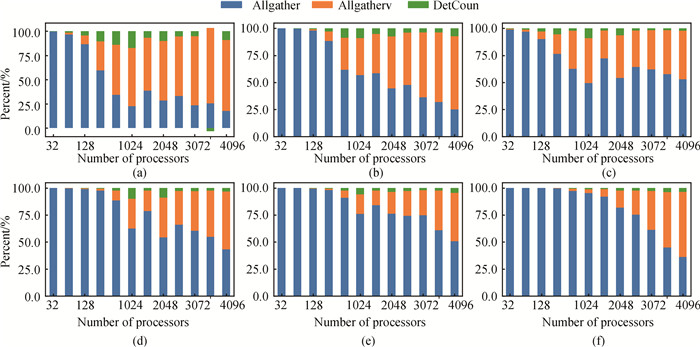
图12 各个算例RAP组件CPkg模块的时间占比随进程数变化趋势图 (a)RHD-1T;(b)RHD-3T;(c)SM-LXJ;(d)SM-C; (e)HF-S;(f)HF-C
Fig.12 The time percentage of the CPkg module in the RAP component for each example with number of processes (a)RHD-1T; (b)RHD-3T; (c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C
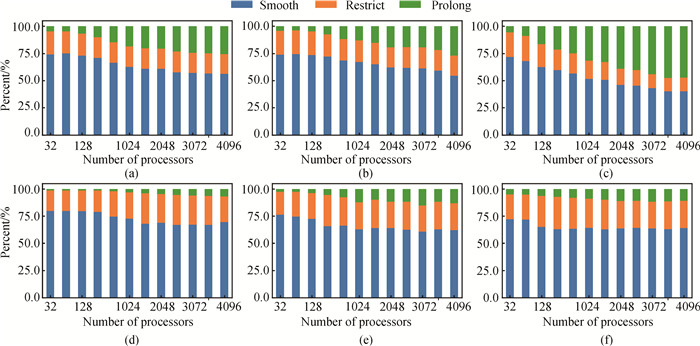
图13 各个算例Cycle模块的时间占比随进程数变化趋势图 (a)RHD-1T;(b)RHD-3T;(c)SM-LXJ;(d)SM-C; (e)HF-S;(f)HF-C
Fig.13 The time percentage of the Cycle module for each example with number of processes (a)RHD-1T; (b)RHD-3T; (c)SM-LXJ; (d)SM-C; (e)HF-S; (f)HF-C
| 层号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 |
| RHD-1T | 6 | 16 | 11 | 8 | 7 | 6 | 42.4 |
| RHD-3T | 7 | 16 | 12 | 8 | 8 | 6 | |
| SM-LXJ | 14 | 20 | 16 | 14 | 14 | 4 | |
| SM-C | 12 | 13 | 10 | 7 | 5 | 1 | |
| HF-S | 16 | 12 | 10 | 10 | 8 | 8 | 5 |
| HF-C | 4 | 10 | 9 | 9 | 8 | 6 | 5 |
表6 各算例在各网格层中插值算子每行非零元数最大值(L0为最细层网格,进程数为4 096。)
Table 6 Maximum number of non-zero elements per row of interpolation operator for each example at each grid level (L0 represents the finest grid layer and the number of processes is 4 096.)
| 层号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 |
| RHD-1T | 6 | 16 | 11 | 8 | 7 | 6 | 42.4 |
| RHD-3T | 7 | 16 | 12 | 8 | 8 | 6 | |
| SM-LXJ | 14 | 20 | 16 | 14 | 14 | 4 | |
| SM-C | 12 | 13 | 10 | 7 | 5 | 1 | |
| HF-S | 16 | 12 | 10 | 10 | 8 | 8 | 5 |
| HF-C | 4 | 10 | 9 | 9 | 8 | 6 | 5 |
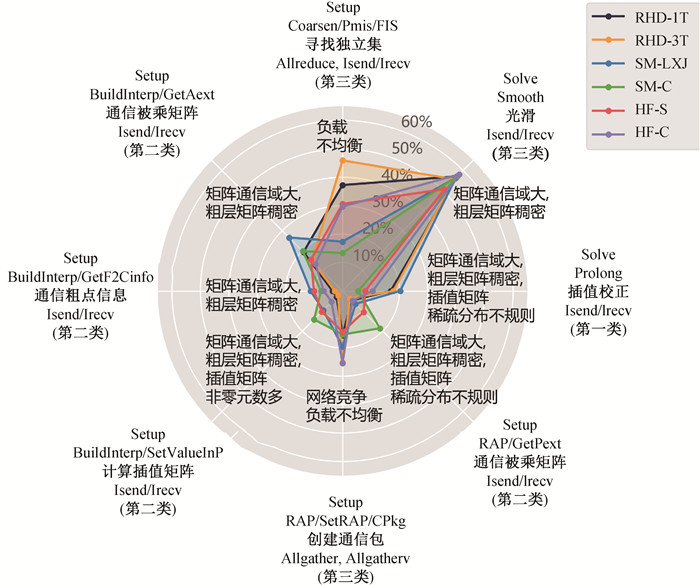
图14 在渐进规模下不同算例的各模块时间占所属阶段(Setup或Solve)的时间百分比雷达图
Fig.14 Radar chart of time percentage for different modules of examples under asymptotic size in each stage (Setup or Solve)
| 1 | BRANDT A. Multi-Level adaptive techniques (MLAT) for partial differential equations: ideas and software[M]//RICE J R. Mathematical Software. New York: Academic Press, 1977: 277-318. |
| 2 | 徐小文, 莫则尧, 安恒斌. 求解大规模稀疏线性代数方程组序列的自适应AMG预条件策略[J]. 中国科学: 信息科学, 2016, 46 (10): 1411- 1420. |
| 3 |
徐小文, 莫则尧, 安恒斌. 求解二维三温辐射扩散方程组的一种代数两层迭代方法[J]. 计算物理, 2009, 26 (1): 1- 8.
DOI |
| 4 |
QIAO Changhe , WU Shuhong , XU Jinchao , et al. Analytical decoupling techniques for fully implicit reservoir simulation[J]. Journal of Computational Physics, 2017, 336, 664- 681.
DOI |
| 5 |
CHEN Junqing , CHEN Zhiming , CUI Tao , et al. An adaptive finite element method for the eddy current model with circuit/field couplings[J]. SIAM Journal on Scientific Computing, 2010, 32 (2): 1020- 1042.
DOI |
| 6 |
周志阳, 徐小文, 舒适, 等. 二维三温辐射扩散方程组两层预条件子的自适应求解[J]. 计算物理, 2012, 29 (4): 475- 483.
DOI |
| 7 |
HENSON V E , YANG U M . BoomerAMG: A parallel algebraic multigrid solver and preconditioner[J]. Applied Numerical Mathematics, 2002, 41 (1): 155- 177.
DOI |
| 8 |
BELL N , OLSON L N , SCHRODER J . PyAMG: Algebraic multigrid solvers in python[J]. Journal of Open Source Software, 2022, 7 (72): 4142.
DOI |
| 9 |
XU Xiaowen , YUE Xiaoqiang , MAO Runzhang , et al. JXPAMG: a parallel algebraic multigrid solver for extreme-scale numerical simulations[J]. CCF Transactions on High Performance Computing, 2023, 5 (1): 72- 83.
DOI |
| 10 |
NAUMOV M , ARSAEV M , CASTONGUAY P , et al. AmgX: A library for GPU accelerated algebraic multigrid and preconditioned iterative methods[J]. SIAM Journal on Scientific Computing, 2015, 37 (5): S602- S626.
DOI |
| 11 | HÄFNER F. Simulation and parameter identification of Oswald's saltpool experiments with the SAMG multigrid-solver in the transport code MODCALIF[C]//Proceedings of the Conference "Finite-Element Models, MODFLOW, and More", 2004: 13-16. |
| 12 | 徐小文. 并行代数多重网格算法: 大规模计算应用现状与挑战[J]. 数值计算与计算机应用, 2019, 40 (4): 243- 260. |
| 13 | YANG U M. Parallel algebraic multigrid methods-high performance preconditioners[M]//Bruaset A M, Tveito A. Numerical Solution of Partial Differential Equations on Parallel Computers. Berlin: Springer, 2006: 209-236. |
| 14 |
MO Zeyao , XU Xiaowen . Relaxed RS0 or CLJP coarsening strategy for parallel AMG[J]. Parallel Computing, 2007, 33 (3): 174- 185.
DOI |
| 15 | GAHVARI H, GROPP W, JORDAN K E, et al. Modeling the performance of an algebraic multigrid cycle using hybrid MPI/OpenMP[C]//2012 41st International Conference on Parallel Processing. Pittsburgh: IEEE, 2012: 128-137. |
| 16 |
BIENZ A , FALGOUT R D , GROPP W , et al. Reducing parallel communication in algebraic multigrid through sparsification[J]. SIAM Journal on Scientific Computing, 2016, 38 (5): S332- S357.
DOI |
| 17 |
MASCAGNI M , BIENZ A , GROPP W D , et al. Reducing communication in algebraic multigrid with multi-step node aware communication[J]. International Journal of High Performance Computing Applications, 2020, 34 (5): 547- 561.
DOI |
| 18 | BAKER A H, SCHULZ M, YANG U M. On the performance of an algebraic multigrid solver on multicore clusters[M]//PALMA J M L M, DAYDÉ M, MARQUES O. High Performance Computing for Computational Science-VECPAR 2010. Berlin: Springer, 2010: 102-115. |
| 19 | BAKER A H, GAMBLIN T, SCHULZ M, et al. Challenges of scaling algebraic multigrid across modern multicore architectures[C]//2011 IEEE International Parallel & Distributed Processing Symposium. Anchorage: IEEE, 2011: 275-286. |
| 20 | PARK J, SMELYANSKIY M, YANG U M, et al. High-performance algebraic multigrid solver optimized for multi-core based distributed parallel systems[C]//Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis. Austin, Texas: Association for Computing Machinery, 2015: 54. |
| 21 |
BRANNICK J J , FALGOUT R D . Compatible relaxation and coarsening in algebraic multigrid[J]. SIAM Journal on Scientific Computing, 2010, 32 (3): 1393- 1416.
DOI |
| 22 |
徐小文, 莫则尧. 并行代数多重网格算法可扩展性能分析[J]. 计算物理, 2007, 24 (4): 387- 394.
DOI |
| 23 | 徐小文, 莫则尧, 曹小林. HYPRE中多重网格解法器的并行可扩展性能分析[J]. 软件学报, 2009, 20 (Z1): 8- 14. |
| 24 | 田鸿运. 大规模数值模拟运行时稳定性评测与诊断[D]. 北京: 中国工程物理研究院, 2022. |
| 25 | YANG U, FALGOUT R, PARK J. Algebraic Multigrid Benchmark[R]. Livermore, CA (United States): Lawrence Livermore National Lab (LLNL), 2017. |
| 26 |
FALGOUT R D , JONES J E , YANG U M . Pursuing scalability for hypre's conceptual interfaces[J]. ACM Transactions on Mathematical Software, 2005, 31 (3): 326- 350.
DOI |
| 27 |
PATARASUK P , YUAN Xin . Bandwidth optimal all-reduce algorithms for clusters of workstations[J]. Journal of Parallel and Distributed Computing, 2009, 69 (2): 117- 124.
DOI |
| 28 | 傅天豪, 田鸿运, 金煜阳, 等. 一种面向构件化并行应用程序的性能骨架分析方法[J]. 计算机科学, 2021, 48 (6): 1- 9. |
| 29 |
ADVE V , SAKELLARIOU R . Application representations for multiparadigm performance modeling of large-scale parallel scientific codes[J]. International Journal of High Performance Computing Applications, 2000, 14 (4): 304- 316.
DOI |
| 30 | SODHI S, SUBHLOK J. Skeleton based performance prediction on shared networks[C]//IEEE International Symposium on Cluster Computing and the Grid, 2004. CCGrid 2004. Chicago: IEEE, 2004: 723-730. |
| 31 |
SODHI S , SUBHLOK J , XU Qiang . Performance prediction with skeletons[J]. Cluster Computing, 2008, 11 (2): 151- 165.
DOI |
| 32 |
VETTER J S , MCCRACKEN M O . Statistical scalability analysis of communication operations in distributed applications[J]. ACM SIGPLAN Notices, 2001, 36 (7): 123- 132.
DOI |
| 33 | DE STERCK H , FALGOUT R D , NOLTING J W , et al. Distance-two interpolation for parallel algebraic multigrid[J]. Numerical Linear Algebra With Applications, 2008, 15 (2/3): 115- 139. |
| 34 | DE STERCKH H , YANG U M , HEYS J J . Reducing complexity in parallel algebraic multigrid preconditioners[J]. SIAM Journal on Matrix Analysis and Applications, 2006, 27 (4): 1019- 1039. |
| 35 | 徐小文, 莫则尧, 武林平. 迭代方法中基于渐近规模的通信与计算比分析[J]. 计算机学报, 2013, 36 (4): 782- 789. |
| [1] | 舒适, 岳孝强, 何剑萌, 徐小文, 莫则尧. 多群辐射扩散问题特征驱动的并行AMG法[J]. 计算物理, 2024, 41(1): 87-97. |
| [2] | 冯春生, 李仕哲, 刘生豪, 张晨松, 赵梨. 面向渗流力学应用特征的预条件方法[J]. 计算物理, 2024, 41(1): 98-109. |
| [3] | 郝悦, 黄思路, 徐小文. 三温能量方程离散线性系统的两层迭代算法收敛因子估计及特征分析[J]. 计算物理, 2024, 41(1): 122-130. |
| [4] | 胡少亮, 许开龙, 徐然, 刘再刚, 徐小文, 安恒斌, 范荣红, 汪振宇, 王伟. 求解压力Poisson方程的混合粗化代数多重网格算法[J]. 计算物理, 2023, 40(5): 527-534. |
| [5] | 胡毅, 安恒斌. 半导体器件数值模拟中电子连续性方程的求解算法[J]. 计算物理, 2023, 40(5): 570-582. |
| [6] | 左风丽, 刘旭, 张宝印, 胡晓燕. 基于JASMIN三维势场快速多极子算法的并行实现[J]. 计算物理, 2013, 30(1): 140-147. |
| [7] | 周志阳, 徐小文, 舒适, 冯春生, 莫则尧. 二维三温辐射扩散方程组两层预条件子的自适应求解[J]. 计算物理, 2012, 29(4): 475-483. |
| [8] | 成杰, 张林波. 一种可扩展的三维半导体器件并行数值模拟算法[J]. 计算物理, 2012, 29(3): 439-448. |
| [9] | 徐小文, 莫则尧, 安恒斌. 求解二维三温辐射扩散方程组的一种代数两层迭代方法[J]. 计算物理, 2009, 26(1): 1-8. |
| [10] | 徐小文, 莫则尧. 并行代数多重网格算法可扩展性能分析[J]. 计算物理, 2007, 24(4): 387-394. |
| [11] | 舒适, 黄云清, 阳莺, 蔚喜军, 肖映雄. 一类三维等代数结构面剖分下的代数多重网格算法[J]. 计算物理, 2005, 22(6): 18-22. |
| [12] | 刘朝霞, 常谦顺. 由扩散张量导出的各向异性扩散模型的隐式数值模拟[J]. 计算物理, 2005, 22(4): 365-370. |
| [13] | 莫则尧, 许林宝, 张宝琳, 沈隆钧. 二维等离子体模拟粒子云网格方法的并行计算与性能分析[J]. 计算物理, 1999, 16(5): 496-504. |
| [14] | 付汉清, 常谦顺. 用代数多重网格法求解一维分裂格式的Euler方程[J]. 计算物理, 1997, 14(1): 19-25. |
| [15] | 常谦顺, 李正锋. 在代数多重网格法中的新插值公式[J]. 计算物理, 1990, 7(4): 453-460. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
