弱耦合导致的再入性心律失常研究

doi:10.19596/j.cnki.1001-246x.8761

摘要/Abstract

摘要：

采用Luo-Rudy相I心脏模型研究点波源产生的波在一维、二维弱耦合心肌组织中的传播, 观察到弱耦合会导致波传播速度减小; 当心肌组织出现大的耦合强度梯度时, 弱耦合会导致波传播受阻和心肌细胞出现早期后除极化; 当心肌细胞之间耦合强度足够低时, 观察到心肌组织会出现波的环形运动和复杂的波传播现象。此外通过构造两种不同耦合结构的二维心肌组织, 研究平面波在二维弱耦合心肌组织中的传播, 结果发现: 平面波在这两种心肌组织中传播时都可自发产生螺旋波, 提高细胞之间耦合强度可有效阻止波的环形运动和螺旋波的自发产生。进一步分析了产生上述现象的物理机制。

关键词: 弱耦合, 心肌缺血, 螺旋波, 心律失常

Abstract:

The Luo Rudy phase I heart model is used in this paper to study the propagation of waves generated by point wave sources in one- and two-dimensional weakly coupled myocardial tissues. It is observed that the weak coupling can lead to the reduction of the wave propagation speed. When there is a large coupling intensity gradient in the myocardial tissue, weak coupling can lead to the frustration of wave propagation and early afterdepolarization showed by cardiomyocytes. When the coupling intensity between cardiomyocytes is low enough, circular motion of wave and complex wave propagation can be observed in myocardial tissues. In addition, we also study the propagation of planar wave in two-dimensional weakly coupled myocardial tissues by constructing two different two-dimensional myocardial tissues with different coupling structures. We find that spiral waves can be spontaneously generated when plane wave propagates in the two myocardial tissues. Increasing the coupling intensity between cells can effectively prevent the circus movement of wave and the spontaneous generation of spiral wave. The physical mechanism of the above phenomenon is analyzed in this paper.

Key words: weak coupling, myocardial ischemia, spiral wave, arrhythmia

中图分类号:

O411.3

韦智杰, 莫玉香, 林榕梅, 兰孝克, 唐国宁. 弱耦合导致的再入性心律失常研究[J]. 计算物理, 2024, 41(5): 670-679.

Zhijie WEI, Yuxiang MO, Rongmei LIN, Xiaoke LAN, Guoning TANG. Study on Reentrant Arrhythmia Caused by Weak Coupling[J]. Chinese Journal of Computational Physics, 2024, 41(5): 670-679.

图/表 8

图1 不同耦合强度下膜电位的时空斑图(a) D1=0.000 2 cm2 ·ms-1; (b) D1=0.000 5 cm2 ·ms-1

Fig.1 Spatiotemporal patterns of membrane potential at different coupling intensities (a) D1=0.000 2 cm2 ·ms-1; (b) D1=0.000 5 cm2 ·ms-1

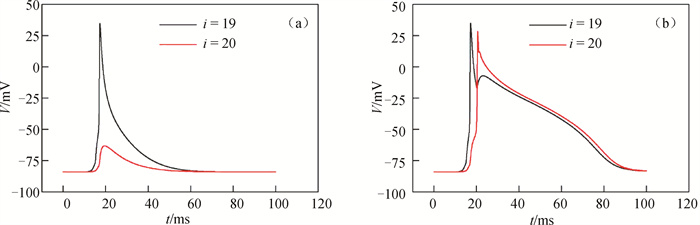
图2 不同耦合强度下弱-强耦合区边界两侧心肌细胞的膜电位随时间的变化(a) D1=0.000 2 cm2 ·ms-1; (b) D1=0.000 5 cm2 ·ms-1

Fig.2 Evolution of membrane potential of cardiomyocytes on both sides of the boundary between weak and strong coupling regions at different coupling intensities (a) D1=0.000 2 cm2 ·ms-1; (b) D1=0.000 5 cm2 ·ms-1

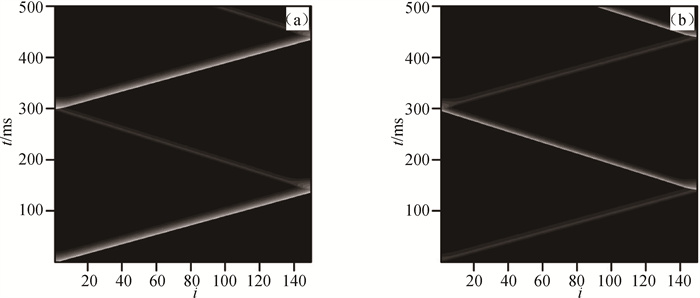
图3 在Dx=0.000 5 cm2 ·ms-1和Dy=0.000 105 cm2 ·ms-1情况下(a)第1行和(b)第2行心肌细胞膜电位的时空斑图

Fig.3 Spatiotemporal patterns of membrane potential of cardiomyocytes in (a) the first row and (b) the second row at Dx=0.000 5 cm2 ·ms-1 and Dy=0.000 105 cm2 ·ms-1

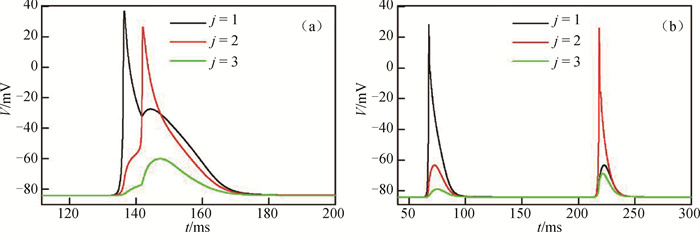
图4 在Dx=0.000 5 cm2 ·ms-1和Dy=0.000 105 cm2 ·ms-1不同格点上的心肌细胞膜电位随时间的变化(a) i=150; (b) i=75

Fig.4 Evolution of cardiomyocytes membrane potential with time at different sites of Dx=0.000 5 cm2 ·ms-1 and Dy=0.000 105 cm2 ·ms-1 (a) i=150; (b) i=75

图5 在Dx=0.000 5 cm2 ·ms-1和Dy=0.000 110 cm2 ·ms-1情况下不同时刻的膜电位斑图(a) t=80 ms; (b) t=145 ms; (c) t=155 ms; (d) t=180 ms; (e) t=200 ms; (f) t=210 ms; (g) t=220 ms; (h)t=250 ms; (i) t=340 ms; (j) t=380 ms; (k) t=420 ms; (l) t=500 ms; (m) t=509 ms; (n) t=540 ms; (o) t=610 ms; (p) t=700 ms

Fig.5 Patterns of membrane potential at different time points with Dy=0.000 5 cm2 ·ms-1 and Dy=0.000 110 cm2 ·ms-1 (a) t=80 ms; (b) t=145 ms; (c) t=155 ms; (d) t=180 ms; (e) t=200 ms; (f) t=210 ms; (g) t =220 ms; (h) t=250 ms; (i) t=340 ms; (j) t=380 ms; (k) t=420 ms; (l) t=500 ms; (m) t=509 ms; (n) t=540 ms; (o) t=610 ms; (p) t=700 ms

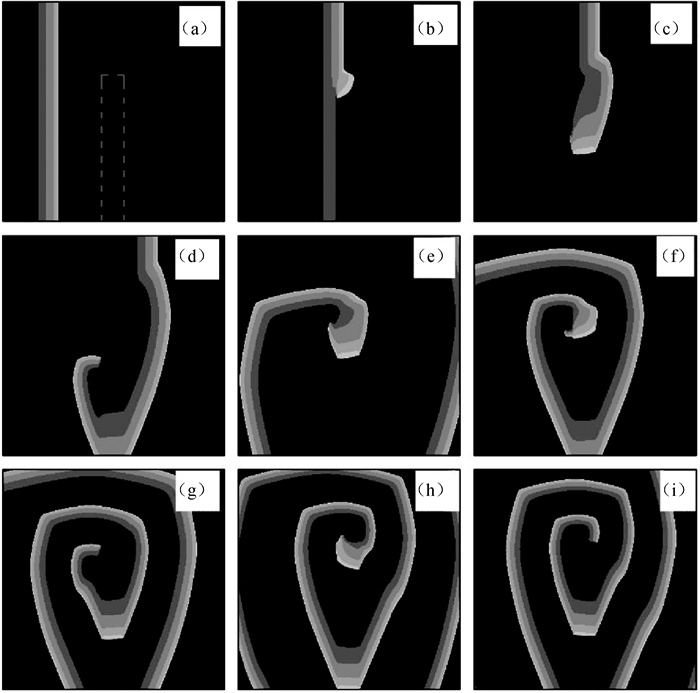
图6 在D2=0.000 25 cm2 ·ms-1情况下不同时刻的膜电位斑图(图(a)中的灰色虚线围成的区域为正常耦合区，其余为弱耦合区。) (a)t=100 ms; (b) t=200 ms; (c) t=240 ms; (d) t=300 ms; (e) t=440 ms; (f) t=520 ms; (g) t=570 ms; (h) t=750 ms; (i) t=800 ms

Fig.6 Patterns of membrane potential at different time points with D2=0.000 25 cm2 ·ms-1 (The region enclosed by the gray dotted line in Fig.(a) is the normal coupling region. The rest is the weak coupling region.) (a) t=100 ms; (b) t=200 ms; (c) t=240 ms; (d) t=300 ms; (e) t=440 ms; (f) t=520 ms; (g) t=570 ms; (h) t=750 ms; (i) t=800 ms

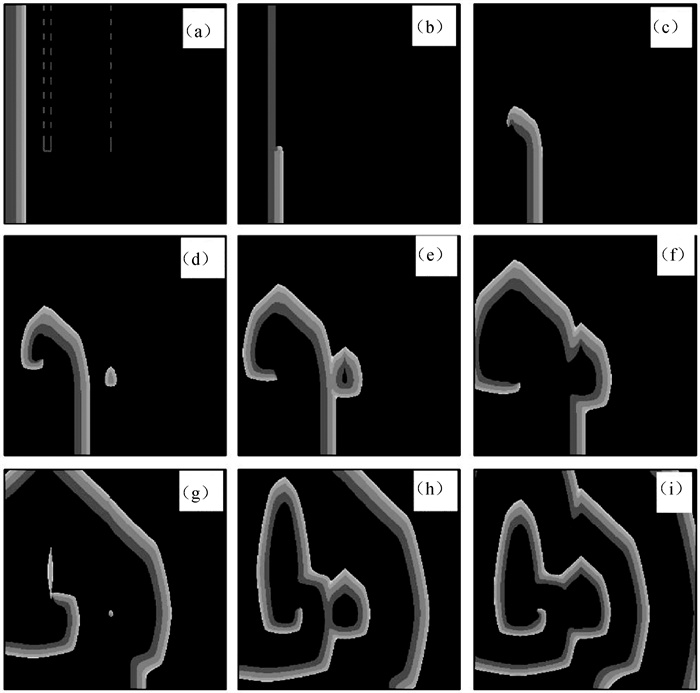
图7 第1层心肌组织在不同时刻的膜电位斑图(灰白色虚线和虚线框内是层间耦合区，对应层间耦合强度分别为D12L=0.000 4 cm2 ·ms-1和D12R=0.001 cm2 ·ms-1。) (a) t=38 ms; (b) t=98 ms; (c) t=156 ms; (d) t=200 ms; (e) t=230 ms; (f) t=263 ms; (g) t=340 ms; (h) t=400 ms; (i) t=510 ms

Fig.7 Patterns of membrane potential in the first layer myocardial tissue at different time points (The gray-white dotted ine and the dotted line box display the interlayer coupling regions, corresponding to interlayer coupling intensities are D12L=0.000 4 cm2 ·ms-1 and D12R=0.001 cm2 ·ms-1, respectively.) (a) t=38 ms; (b) t=98 ms; (c) t=156 ms; (d) t=200 ms; (e) t=230 ms; (f) t=263 ms; (g) t=340 ms; (h) t=400 ms; (i) t=510 ms

图8 第2层心肌组织在不同时刻的膜电位斑图(灰白色虚线和虚线框内是层间耦合区，对应层间耦合强度分别为D12L=0.000 4 cm2 ·ms-1和D12R=0.001 cm2 ·ms-1。) (a) t=38 ms; (b) t=98 ms; (c) t=156 ms; (d) t=200 ms; (e) t=230 ms; (f) t=263 ms; (g) t =340 ms; (h) t=400 ms; (i) t=510 ms

Fig.8 Patterns of membrane potential in the second layer myocardial tissue at different time points (The gray-white dotted line and the dotted line box display the interlayer coupling regions, corresponding to interlayer coupling intensities are D12L=0.0004 cm2 ·ms-1 and D12R=0.001 cm2 ·ms-1, respectively.) (a) t=38 ms; (b) t=98 ms; (c) t=156 ms; (d) t=200 ms; (e) t=230 ms; (f) t=263 ms; (g) t =340 ms; (h) t=400 ms; (i) t=510 ms

参考文献 25

1	XIE Y F , SATO D , GARFINKEL A , et al. So little source, so much sink: Requirements for afterdepolarizations to propagate in tissue[J]. Biophysical Journal, 2010, 99 (5): 1408- 1415. DOI
2	ANTZELEVITCH C . Basic mechanisms of reentrant arrhythmias[J]. Current Opinion in Cardiology, 2001, 16 (1): 1- 7. DOI
3	KRISHNAN S C , ANTZELEVITCH C . Flecainide-induced arrhythmia in canine ventricular epicardium. Phase 2 reentry?[J]. Circulation, 1993, 87 (2): 562- 572. DOI
4	HOLMQVIST F , KESEK M , ENGLUND A , et al. A decade of catheter ablation of cardiac arrhythmias in Sweden: Ablation practices and outcomes[J]. European Heart Journal, 2019, 40 (10): 820- 830. DOI
5	RAZMINIA M , WILLOUGHBY M C , DEMO H , et al. Fluoroless catheter ablation of cardiac arrhythmias: A 5-Year experience[J]. Pacing and Clinical Electrophysiology: PACE, 2017, 40 (4): 425- 433. DOI
6	MARROUCHE N F , BRACHMANN J , ANDRESEN D , et al. Catheter ablation for atrial fibrillation with heart failure[J]. The New England Journal of Medicine, 2018, 378 (5): 417- 427. DOI
7	白婧, 黄志精, 唐国宁. 用运动控制器来终止心律失常[J]. 计算物理, 2021, 38 (3): 352- 360.
8	PERTSOV A M , DAVIDENKO J M , SALOMONSZ R , et al. Spiral waves of excitation underlie reentrant activity in isolated cardiac muscle[J]. Circulation Research, 1993, 72 (3): 631- 650. DOI
9	DAVIDENKO J M . Spiral wave activity: A possible common mechanism for polymorphic and monomorphic ventricular tachycardias[J]. Journal of Cardiovascular Electrophysiology, 1993, 4 (6): 730- 746. DOI
10	关富荣, 李成乾, 邓敏艺. 激发介质相对不应态对螺旋波动力学行为的影响[J]. 计算物理, 2021, 38 (6): 749- 756.
11	DAVIDENKO J M , PERTSOV A V , SALOMONSZ R , et al. Stationary and drifting spiral waves of excitation in isolated cardiac muscle[J]. Nature, 1992, 355 (6358): 349- 351. DOI
12	ZIMIK S , PANDIT R . Reentry via high-frequency pacing in a mathematical model for human-ventricular cardiac tissue with a localized fibrotic region[J]. Scientific Reports, 2017, 7, 15350. DOI
13	ZEMLIN CW , PERTSOV AM . Bradycardic onset of spiral wave re-entry: Structural substrates[J]. Europace, 2017, 9 (suppl 6): vi59- vi63.
14	HUFFAKER R , LAMP S T , WEISS J N , et al. Intracellular calcium cycling, early afterdepolarizations, and reentry in simulated long QT syndrome[J]. Heart Rhythm, 2004, 1 (4): 441- 448. DOI
15	WEISS J N , GARFINKEL A , KARAGUEUZIAN H S , et al. Early afterdepolarizations and cardiac arrhythmias[J]. Heart Rhythm, 2010, 7 (12): 1891- 1899. DOI
16	BERNUS O , ZEMLIN C W , ZARITSKY R M , et al. Alternating conduction in the ischaemic border zone as precursor of reentrant arrhythmias: A simulation study[J]. Europace, 2005, 7 Suppl 2, 93- 104.
17	CLAYTON RH , TAGGART P . Regional differences in APD restitution can initiate wavebreak and re-entry in cardiac tissue: A computational study[J]. Biomedical Engineering Online, 2005, 4, 54- 67. DOI
18	NAKAGAMI T , TANAKA H , DAI Ping , et al. Generation of reentrant arrhythmias by dominant-negative inhibition of connexin43 in rat cultured myocyte monolayers[J]. Cardiovascular Research, 2008, 79 (1): 70- 79. DOI
19	ZIPES D P , WELLENS H J J . Sudden cardiac death[J]. Circulation, 1998, 98, 2334- 21351. DOI
20	DE GROOT JR , CORONEL R . Acute ischemia-induced gap junctional uncoupling and arrhythmogenesis[J]. Cardiovascular Research, 2004, 62 (2): 323- 334. DOI
21	KLÉBER A G , RIEGGER C B , JANSE M J . Electrical uncoupling and increase of extracellular resistance after induction of ischemia in isolated, arterially perfused rabbit papillary muscle[J]. Circulation Research, 1987, 61 (2): 271- 279. DOI
22	MA J . Biophysical neurons, energy, and synapse controllability: a review[J]. Journal of Zhejiang University-Science A, 2022, (24): 109- 129.
23	黄志精, 白婧, 唐国宁. 单向耦合神经元网络中螺旋波的自发形成机制[J]. 计算物理, 2020, 37 (5): 612- 622.
24	LUO C H , RUDY Y . A model of the ventricular cardiac action potential. Depolarization, repolarization, and their interaction[J]. Circulation Research, 1991, 68, 1501- 1526. DOI
25	李倩昀, 白婧, 唐国宁. 两层老化心肌组织中螺旋波和时空混沌的控制[J]. 物理学报, 2021, 70 (9): 349- 359.

[1]	王国威, 付燕. 随机边界诱导Izhikevich神经元网络的时空模式转换[J]. 计算物理, 2023, 40(5): 622-632.
[2]	李成乾, 关富荣, 邓敏艺. 传导阻滞和折返效应对螺旋波演化行为的影响[J]. 计算物理, 2023, 40(1): 117-126.
[3]	陈绍英, 王雪丽, 高志梅, 袁国勇. 环域反馈下复Ginzburg-Landau系统的螺旋波动力学行为[J]. 计算物理, 2022, 39(1): 118-126.
[4]	杜丹, 李帅, 阳璞琼, 冯军, 向东, 龚学余. 螺旋天线轴向长度对螺旋波传播、吸收的影响[J]. 计算物理, 2021, 38(6): 713-721.
[5]	关富荣, 李成乾, 邓敏艺. 激发介质相对不应态对螺旋波动力学行为的影响[J]. 计算物理, 2021, 38(6): 749-756.
[6]	白婧, 黄志精, 唐国宁. 用运动控制器来终止心律失常[J]. 计算物理, 2021, 38(3): 352-360.
[7]	黄志精, 白婧, 唐国宁. 单向耦合神经元网络中螺旋波的自发形成机制[J]. 计算物理, 2020, 37(5): 612-622.
[8]	张学良, 谭惠丽, 唐国宁, 邓敏艺. 心肌组织机械形变的元胞自动机模拟[J]. 计算物理, 2018, 35(3): 294-302.
[9]	杨翠云, 刘海英, 唐国宁. 两阶段脉冲控制螺旋波的数值模拟[J]. 计算物理, 2014, 31(5): 625-630.
[10]	陈茜琼, 邓敏艺, 唐国宁, 孔令江. 传导延迟对螺旋波动力学行为的影响[J]. 计算物理, 2013, 30(4): 620-626.
[11]	陈绍英, 袁国勇, 吴刚, 崔倩倩, 范红领. Lévy噪声与周期力共同驱动下的螺旋波动力学[J]. 计算物理, 2012, 29(4): 620-626.
[12]	黎广钊, 唐国宁. 激发介质中去极化对螺旋波动力学影响的数值研究[J]. 计算物理, 2011, 28(4): 626-632.
[13]	钟敏, 唐国宁. 通过控制钙和钾离子流抑制心脏中的螺旋波和时空混沌[J]. 计算物理, 2011, 28(1): 119-124.
[14]	马军, 吴宁杰, 应和平, 蒲忠胜. 局部相空间压缩实现对时空混沌和螺旋波的控制[J]. 计算物理, 2006, 23(2): 243-248.
[15]	闫广武. 激励介质中非线性化学波的格子Boltzmann模型[J]. 计算物理, 2003, 20(4): 356-358.