Study on Braess Paradox of Power Grid Based on Complex Network Topology

doi:10.19596/j.cnki.1001-246x.8653

Abstract

Abstract:

To explore a better power grid structure and reduce the probability of Braess paradox. In this paper, the second order Kuramoto-like phase oscillator model is used to reasonably model the power grid, and several networks are generated by ER random model in which the number of network nodes and links is the same as IEEE14, IEEE30, and IEEE39, respectively. By increasing the number of generator nodes and changing the position of generators in the random network, the occurrence probability of Braess paradox caused by a new adding transmission lines in the different power grid is studied. Study shows that appropriately increasing the number of generator nodes in the power grid can reduce the probability of the Braess paradox in the power grid, and taking large-degree nodes as generator nodes is beneficial to improve the power grid synchronizability and reduce the probability of Braess paradox. This study has certain guiding significance for the topology design and optimization of the power grid.

Key words: complex network, topological structure, synchronization performance, Braess paradox

CLC Number:

TM711

Beibei SHAO, Yanli ZOU, Shaoyan HONG, Chanjuan LIANG. Study on Braess Paradox of Power Grid Based on Complex Network Topology[J]. Chinese Journal of Computational Physics, 2023, 40(6): 770-778.

Figures/Tables 11

Table 1 The steady state frequency offset and the critical synchronous coupling strength of the original network of IEEE14 system and the network after the addition of some transmission lines

新增传输线路编号	稳态频偏	临界同步耦合强度
原网络	0.0	2.3
(1, 3)	0.0	2.3
(1, 4)	0.0	2.2
(2, 7)	2.6	2.4
(3, 10)	2.6	2.5
(3, 14)	0.0	2.2
(5, 8)	0.0	2.3
(5, 11)	2.6	2.5
(6, 8)	0.0	2.0
(8, 14)	0.0	1.9

Table 2 Three kinds of standard test system characteristics parameters

系统	总节点数	连边数	网络节点平均度
IEEE14	14	20	2.857 1
IEEE30	30	41	2.733 3
IEEE39	39	46	2.359 0

Table 3 Allocation of the number of generators and load nodes in a 14-node network

	14节点网络
发电机节点个数	1	3	5	7
负载节点个数	13	11	9	7

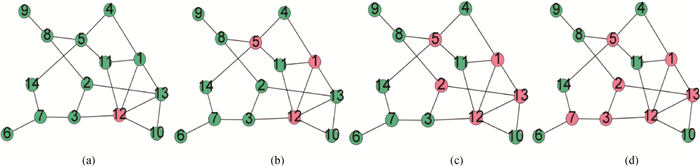
Fig.1 Degree distribution of nodes (a), (b), (c) corresponding to network 1, 2 and 3, respectively

Fig.2 Topology of large degree nodes as generators (a), (b), (c) and (d) corresponding to a network with one, three, five and seven generator nodes, respectively

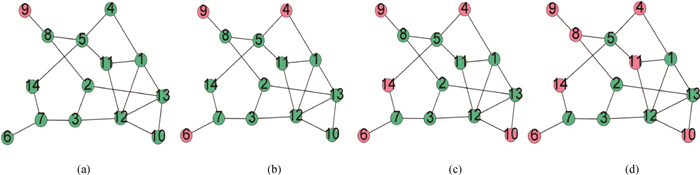
Fig.3 Topology of small degree nodes as generators, (a), (b), (c) and (d) corresponding to a network with one, three, five and seven generator nodes, respectively

Fig.4 The proportion of lines with Kc increasing, decreasing or unchanging after adding a new transmission line to a 14-node network varies with the number of generator nodes (a) large degree nodes as generators in a 14-node network; (b) small degree nodes as generators in a 14-node network

Table 4 Allocation of the number of generators and load nodes in a 30-node network

	30节点网络
发电机节点个数	3	5	7	15
负载节点个数	27	25	23	15

Table 5 Allocation of the number of generators and load nodes in a 39-node network

	39节点网络
发电机节点个数	3	7	12	19
负载节点个数	36	32	27	20

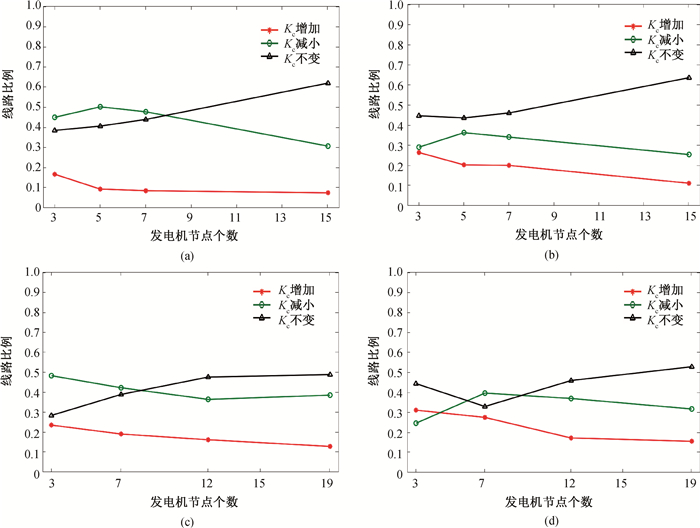
Fig.5 The proportion of lines with Kc increasing, decreasing or unchanging after adding a new transmission line to a 30-node or a 39-node network varies with the number of generator nodes (a)large degree nodes as generators in a 30-node network; (b)small degree nodes as generators in a 30-node network; (c)large degree nodes as generators in a 39-node network; (d)small degree nodes as generators in a 39-node network

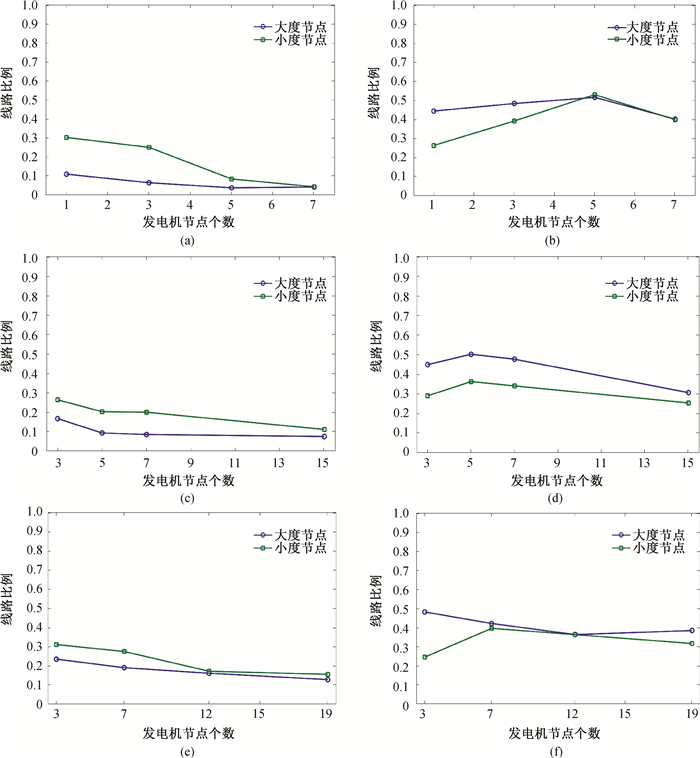
Fig.6 The proportion of lines with Kc increasing and decreasing varies with the number of generators after adding a new transmission line in 14, 30, and 39-node networks, where generators are on large degree nodes or small degree nodes, respectively (a), (c) and (e) denote the proportion of lines with Kc increasing; (b), (d) and (f)denote the proportion of lines with Kc deceasing ((a) and (b)14-node network. (c) and (d)30-node network. (e) and (f)39-node network)

References 26

1	BRAESS D . Vber ein paradoxon aus der verkehrsplanung[J]. Mathematical Methods of Operational Research, 1968, 12 (1): 258- 268. DOI
2	ZHAO C X . Braess' paradox and robustness of traffic network under dynamic equilibrium[J]. WSEAS Transactions on Systems and Control, 2017, 12, 288- 296.
3	赵春雪, 傅白白, 王天明. 拥挤交通网络的Braess'悖论现象[J]. 交通运输系统工程与信息, 2012, 12 (4): 155- 160. DOI
4	MA J , LI D W , C L , et al. Link restriction: Methods of testing and avoiding Braess paradox in networks considering traffic demands[J]. Journal of Transportation Engineering, 2018, 144 (2): 04017076. DOI
5	WANG A H , TANG Y H , MOHMAND Y T , et al. Modifying link capacity to avoid Braess paradox considering elastic demand[J]. Physica A: Statistical Mechanics and Its Applications, 2022, 605, 127951. DOI
6	COLETTA T , JACQUOD P . Linear stability and the Braess paradox in coupled Oscillators networks and electric power grids[J]. Physical Review E, 2016, 93 (3): 032222. DOI
7	张玥, 谢光龙, 张全, 等. 美国得州2 ·15大停电事故分析及对中国电力发展的启示[J]. 中国电力, 2021, 54 (4): 192-198+206.
8	卢恩, 鲁晓军, 龙霏, 等. 电力系统停电风险评估指标及方法[J]. 电力自动化设备, 2015, 35 (3): 68- 74.
9	WITTHAUT D , TIMME M . Nonlocal failures in complex supply networks by single link additions[J]. The European Physical Journal B, 2013, 86 (9): 1- 12.
10	CHAO Y , YI C , LI P , et al. Impact of the network structure on transmission dynamics in complex networks[J]. IFAC Proceedings Volumes, 2013, 46 (13): 218- 223. DOI
11	CETINAY H , KUIPERS F A , Van MIEGHEM P . A topological investigation of power flow[J]. IEEE Systems Journal, 2018, 12 (3): 2524- 2532. DOI
12	FAZLYAB M , DÖRFLER F , PRECIADO V M . Optimal network design for synchronization of coupled oscillators[J]. Automatica, 2017, 84, 181- 189. DOI
13	TCHAWOU T E B , GOMILA D , PERE C , et al. Curing Braess' paradox by secondary control in power grids[J]. New Journal of Physics, 2018, 20 (8): 083005. DOI
14	YANG L X , JIANG J , LIU X J . Influence of edge additions on the synchronizability of oscillatory power networks[J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 41, 11- 18. DOI
15	YANG L X , JIANG J . Impacts of link addition and removal on synchronization of an elementary power network[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 479, 99- 107. DOI
16	KAISER F N. Resilience of power grids and other supply networks: Structural stability, cascading failures and optimal topologies[D]. Koln: Universität zu Köln, 2022.
17	ZOU Y L , WANG R R , GAO Z . Improve synchronizability of a power grid through power allocation and topology adjustment[J]. Physica A: Statistical Mechanics and Its Applications, 2020, 548, 122956. DOI
18	ZOU Y L , L H Q . Study on power grid partition and attack strategies based on complex networks[J]. Frontiers in Physics, 2022, 9, 790218. DOI
19	汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用[M]. 北京: 清华大学出版社, 2006.
20	蔡泽祥, 王星华, 任晓娜. 复杂网络理论及其在电力系统中的应用研究综述[J]. 电网技术, 2012, 36 (11): 114- 121.
21	魏震波, 苟竞. 复杂网络理论在电网分析中的应用与探讨[J]. 电网技术, 2015, 39 (1): 279- 287.
22	LI H Q , ZOU Y L , ZHANG S Z , et al. Robustness of power grids structure and braess paradox phenomenon: A complex network theory study[J]. Chinese Journal of Computational Physics, 2021, 38 (4): 470- 478.
23	ZOU Y L , WANG R R , WU L J , et al. Optimization of synchronization performance in power grids with local order parameters[J]. Chinese Journal of Computational Physics, 2019, 36 (4): 498- 504.
24	FILATRELLA G , NIELSEN A H , PEDERSEN N F . Analysis of a power grid using a Kuramoto-like model[J]. European Physical Journal B Condensed Matter, 2008, 61 (4): 485- 491.
25	ZHANG S Z , ZOU Y L , TAN S Y , et al. Study of Braess paradox in an interconnected power grid based on complex network theory[J]. Chinese Journal of Computational Physics, 2022, 39 (2): 233- 243.
26	GILBERT E N . Random graphs[J]. The Annals of Mathematical Statistics, 1959, 30 (4): 1141- 1144.

[1]	Tao FU, Long WU, Chenguang LI. Site-bond Percolation Modeling of Real Networks: Generating Function Method [J]. Chinese Journal of Computational Physics, 2022, 39(2): 212-222.
[2]	Shaoze ZHANG, Yanli ZOU, Shuyi TAN, Haoqian LI, Xinyan LIU. Analysis of Braess Paradox in an Interconnected Power Grid Based on Complex Network Theory [J]. Chinese Journal of Computational Physics, 2022, 39(2): 233-243.
[3]	Haoqian LI, Yanli ZOU, Shaoze ZHANG, Xinyan LIU, Shuyi TAN. Robustness of Power Grids Structure and Braess Paradox Phenomenon: A Complex Network Theory Study [J]. Chinese Journal of Computational Physics, 2021, 38(4): 470-478.
[4]	LIU Lihua, WEI Duqu, ZHANG Bo. Synchronization Control of Chaos in Complex Motor Networks with Small-world Topology Based on Dynamic Relaying [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(6): 750-756.
[5]	WANG Yi, ZOU Yanli, HUANG Li, LI Ke. Key Nodes Identification of Power Grid Considering Local and Global Characteristics [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(1): 119-126.
[6]	AN haigang. Linkage Fluctuation in Double Variables of Time Series Based on Complex Networks [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2014, 31(6): 742-750.
[7]	FAN Wenli, LIU Zhigang. An Evaluation Method for Node Importance Based on Efficiency Matrix [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2013, 30(5): 714-719.
[8]	TANG Shengxue, CHEN Li, HUANG Jiaoying. Modeling and Identification of Associated Complex Networks [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2012, 29(2): 308-316.
[9]	DANG Huixue, CHEN Zhimin, YANG Zhichun. Merging of Vortex Pair at Different Separating Distances [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2008, 25(3): 259-262.