Chinese Journal of Computational Physics ›› 2025, Vol. 42 ›› Issue (2): 211-223.DOI: 10.19596/j.cnki.1001-246x.8878
• Research Reports • Previous Articles Next Articles
Tong XU( ), Yueqiang SHANG*(
), Yueqiang SHANG*( )
)
Received:2023-12-21
Online:2025-03-25
Published:2025-04-08
Contact:
Yueqiang SHANG
Tong XU, Yueqiang SHANG. Finite Element Iterative Algorithms for Steady Stokes Equations with Nonlinear Damping Term[J]. Chinese Journal of Computational Physics, 2025, 42(2): 211-223.
Add to citation manager EndNote|Ris|BibTeX
URL: http://www.cjcp.org.cn/EN/10.19596/j.cnki.1001-246x.8878
| 算法 | 1/h | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | UH1 | PL2 |
| Stokes迭代 | 20 | 0.335 | 3 | 2.095 04 × 10-4 | 7.905 69 × 10-4 | ||
| 30 | 0.745 | 3 | 9.342 65 × 10-5 | 3.513 64 × 10-4 | 1.991 71 | 2 | |
| 40 | 1.43 | 3 | 5.261 72 × 10-5 | 1.976 42 × 10-4 | 1.995 72 | 2 | |
| 50 | 2.418 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.997 38 | 2 | |
| 60 | 3.659 | 3 | 2.340 67 × 10-5 | 8.784 10 × 10-5 | 1.998 23 | 2 | |
| 70 | 5.409 | 3 | 1.720 01 × 10-5 | 6.453 63 × 10-5 | 1.998 72 | 2 | |
| Oseen迭代 | 20 | 0.236 | 2 | 2.095 04 × 10-4 | 7.905 69 × 10-4 | ||
| 30 | 0.538 | 2 | 9.342 65 × 10-5 | 3.513 64 × 10-4 | 1.991 71 | 2 | |
| 40 | 1.033 | 2 | 5.261 72 × 10-5 | 1.976 42 × 10-4 | 1.995 72 | 2 | |
| 50 | 1.748 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.997 38 | 2 | |
| 60 | 2.64 | 2 | 2.340 67 × 10-5 | 8.784 1 × 10-5 | 1.998 23 | 2 | |
| 70 | 4.012 | 2 | 1.720 01 × 10-5 | 6.453 63 × 10-5 | 1.998 72 | 2 |
Table 1 Errors of Stokes iterative algorithm and Oseen iterative algorithm in 2D (ν=0.01, α=0.1)
| 算法 | 1/h | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | UH1 | PL2 |
| Stokes迭代 | 20 | 0.335 | 3 | 2.095 04 × 10-4 | 7.905 69 × 10-4 | ||
| 30 | 0.745 | 3 | 9.342 65 × 10-5 | 3.513 64 × 10-4 | 1.991 71 | 2 | |
| 40 | 1.43 | 3 | 5.261 72 × 10-5 | 1.976 42 × 10-4 | 1.995 72 | 2 | |
| 50 | 2.418 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.997 38 | 2 | |
| 60 | 3.659 | 3 | 2.340 67 × 10-5 | 8.784 10 × 10-5 | 1.998 23 | 2 | |
| 70 | 5.409 | 3 | 1.720 01 × 10-5 | 6.453 63 × 10-5 | 1.998 72 | 2 | |
| Oseen迭代 | 20 | 0.236 | 2 | 2.095 04 × 10-4 | 7.905 69 × 10-4 | ||
| 30 | 0.538 | 2 | 9.342 65 × 10-5 | 3.513 64 × 10-4 | 1.991 71 | 2 | |
| 40 | 1.033 | 2 | 5.261 72 × 10-5 | 1.976 42 × 10-4 | 1.995 72 | 2 | |
| 50 | 1.748 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.997 38 | 2 | |
| 60 | 2.64 | 2 | 2.340 67 × 10-5 | 8.784 1 × 10-5 | 1.998 23 | 2 | |
| 70 | 4.012 | 2 | 1.720 01 × 10-5 | 6.453 63 × 10-5 | 1.998 72 | 2 |
| 算法 ν | Stokes迭代 | Oseen迭代 | |||||||
| CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | ||
| 10-2 | 2.422 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 2.015 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10-3 | 3.073 | 4 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 2.43 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10-4 | 5.584 | 8 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 4.227 | 6 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
Table 2 Numerical results of Stokes iterative algorithm and Oseen iterative algorithm with different ν (h=1/50, α=0.1)
| 算法 ν | Stokes迭代 | Oseen迭代 | |||||||
| CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | ||
| 10-2 | 2.422 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 2.015 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10-3 | 3.073 | 4 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 2.43 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10-4 | 5.584 | 8 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 4.227 | 6 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 算法 α | Stokes迭代 | Oseen迭代 | |||||||
| CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | ||
| 10-2 | 1.898 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.824 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10-1 | 2.481 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.834 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 1 | 3.139 | 4 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 2.464 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10 | 5.985 | 8 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 4.221 | 6 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 102 | 不收敛 | 13.762 | 21 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | ||||
Table 3 Numerical results of Stokes iterative algorithm and Oseen iterative algorithm with different α (h=1/50, ν=0.01)
| 算法 α | Stokes迭代 | Oseen迭代 | |||||||
| CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | ||
| 10-2 | 1.898 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.824 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10-1 | 2.481 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.834 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 1 | 3.139 | 4 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 2.464 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10 | 5.985 | 8 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 4.221 | 6 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 102 | 不收敛 | 13.762 | 21 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | ||||
| 算法 | 1/h | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | UH1 | PL2 |
| Stokes迭代 | 4 | 2.121 | 9 | 3.998 29 | 1.619 09 × 10-2 | ||
| 6 | 6.699 | 4 | 1.363 89 | 7.195 61 × 10-3 | 2.652 57 | 2.000 12 | |
| 8 | 24.998 | 3 | 6.071 14 × 10-1 | 4.043 94 × 10-3 | 2.813 46 | 2.003 08 | |
| 10 | 96.683 | 3 | 3.201 99 × 10-1 | 2.586 44 × 10-3 | 2.867 10 | 2.002 92 | |
| 12 | 292.779 | 3 | 1.888 57 × 10-1 | 1.795 36 × 10-3 | 2.895 73 | 2.002 39 | |
| Oseen迭代 | 4 | 1.177 | 5 | 3.998 29 | 1.619 09 × 10-2 | ||
| 6 | 5.24 | 3 | 1.363 89 | 7.195 61 × 10-3 | 2.652 57 | 2.000 12 | |
| 8 | 24.364 | 3 | 6.071 14 × 10-1 | 4.043 94 × 10-3 | 2.81 346 | 2.003 08 | |
| 10 | 96.116 | 3 | 3.201 99 × 10-1 | 2.586 44 × 10-3 | 2.867 10 | 2.002 92 | |
| 12 | 289.645 | 3 | 1.888 57 × 10-1 | 1.795 36 × 10-3 | 2.895 73 | 2.002 39 |
Table 4 Errors between Stokes iterative algorithm and Oseen iterative algorithm in 3D (ν=0.001, α=0.1)
| 算法 | 1/h | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | UH1 | PL2 |
| Stokes迭代 | 4 | 2.121 | 9 | 3.998 29 | 1.619 09 × 10-2 | ||
| 6 | 6.699 | 4 | 1.363 89 | 7.195 61 × 10-3 | 2.652 57 | 2.000 12 | |
| 8 | 24.998 | 3 | 6.071 14 × 10-1 | 4.043 94 × 10-3 | 2.813 46 | 2.003 08 | |
| 10 | 96.683 | 3 | 3.201 99 × 10-1 | 2.586 44 × 10-3 | 2.867 10 | 2.002 92 | |
| 12 | 292.779 | 3 | 1.888 57 × 10-1 | 1.795 36 × 10-3 | 2.895 73 | 2.002 39 | |
| Oseen迭代 | 4 | 1.177 | 5 | 3.998 29 | 1.619 09 × 10-2 | ||
| 6 | 5.24 | 3 | 1.363 89 | 7.195 61 × 10-3 | 2.652 57 | 2.000 12 | |
| 8 | 24.364 | 3 | 6.071 14 × 10-1 | 4.043 94 × 10-3 | 2.81 346 | 2.003 08 | |
| 10 | 96.116 | 3 | 3.201 99 × 10-1 | 2.586 44 × 10-3 | 2.867 10 | 2.002 92 | |
| 12 | 289.645 | 3 | 1.888 57 × 10-1 | 1.795 36 × 10-3 | 2.895 73 | 2.002 39 |
| 算法 ν | Stokes迭代 | Oseen迭代 | |||
| CPU/s | it | CPU/s | it | ||
| 10-3 | 6.998 | 20 | 3.345 | 9 | |
| 10-4 | 不收敛 | 不收敛 | 6.809 | 19 | |
Table 5 Numerical results of Stokes iteration and Oseen iteration with different ν
| 算法 ν | Stokes迭代 | Oseen迭代 | |||
| CPU/s | it | CPU/s | it | ||
| 10-3 | 6.998 | 20 | 3.345 | 9 | |
| 10-4 | 不收敛 | 不收敛 | 6.809 | 19 | |
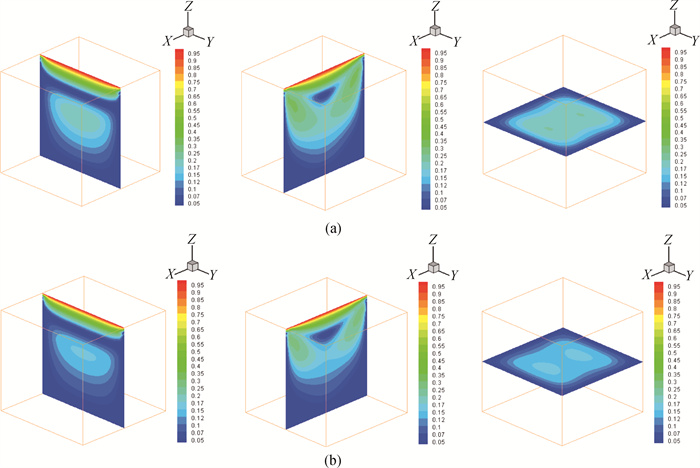
Fig.2 Computed velocity for 3D square cavity driven flow by Oseen iterative algorithm with different values of ν (left: X plane, middle: Y plane, right: Z plane) (a) ν=10-2; (b) ν=10-3
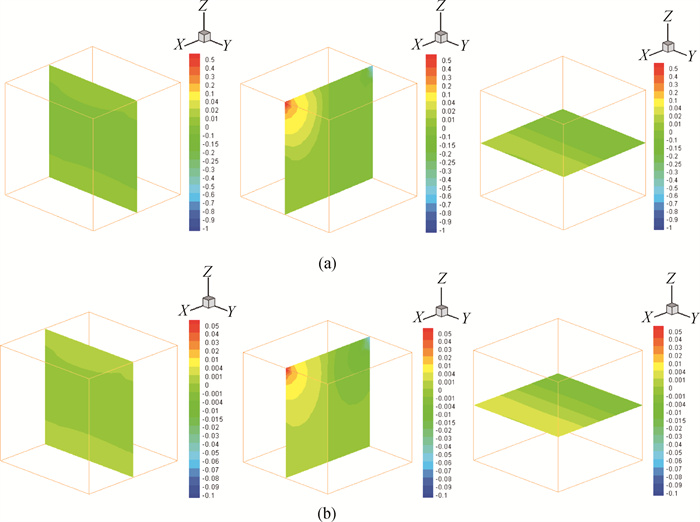
Fig.3 Computed pressure for 3D square cavity driven flow by Oseen iterative algorithm with different values of ν (left: X plane, middle: Y plane, right: Z plane) (a) ν=10-2; (b) ν=10-3
| 1 |
DOI |
| 2 |
DOI |
| 3 |
DOI |
| 4 |
DOI |
| 5 |
DOI |
| 6 |
DOI |
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
王雅莉, 郑波, 尚月强. 定常不可压Navier-Stokes方程的两水平grad-div稳定化有限元方法[J]. 计算物理, 2024, 41(4): 418- 425.
DOI |
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
DOI |
| 15 |
DOI |
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
TEMAM R. Navier-stokes equations: theory and numerical analysis[M]. Amsterdam, New York: North-Holland Pub. Co., 1984.
|
| 22 |
DOI |
| 23 |
DOI |
| 24 |
DOI |
| 25 |
|
| 26 |
DOI |
| 27 |
|
| [1] | Tengfei ZHAO, Hua ZHANG. Study on Instability of Viscoelastic Liquid Jet in Homogeneous Wind Field [J]. Chinese Journal of Computational Physics, 2025, 42(1): 1-9. |
| [2] | Linmao YIN, Yulong ZHANG, Yang YANG, Fujian XIAO, Bingyan JIANG. Velocity-correction Schemes for Solving Incompressible Navier-Stokes Equations Based on Picard Iteration [J]. Chinese Journal of Computational Physics, 2025, 42(1): 10-17. |
| [3] | Yali WANG, Bo ZHENG, Yueqiang SHANG. Two-level Grad-div Stabilized Finite Element Methods for Steady Incompressible Navier-Stokes Equations [J]. Chinese Journal of Computational Physics, 2024, 41(4): 418-425. |
| [4] | Ji CHEN, Yi XU, Jinfu LIU, Tao LIU. Dynamics and Implementation of Memristive System Exhibiting Extreme Multistability [J]. Chinese Journal of Computational Physics, 2024, 41(4): 523-534. |
| [5] | Xiaowen XU, Zeyao MO, Shaoliang HU, Hengbin AN. Feature-modified Algorithm Framework for Parallel Preconditioning in Sparse Linear Solvers [J]. Chinese Journal of Computational Physics, 2024, 41(1): 64-74. |
| [6] | Yue HAO, Silu HUANG, Xiaowen XU. Convergence Estimation and Characteristic Analysis of A Two-level Iterative Algorithm for Discretized Three-temperature Energy Linear Systems [J]. Chinese Journal of Computational Physics, 2024, 41(1): 122-130. |
| [7] | Shaoliang HU, Kailong XU, Ran XU, Zaigang LIU, Xiaowen XU, Hengbin AN, Ronghong FAN, Zhenyu WANG, Wei WANG. A Algebraic Multigrid Algorithm Based on Hybrid Coarsening for Pressure Poisson Equation [J]. Chinese Journal of Computational Physics, 2023, 40(5): 527-534. |
| [8] | Guoliang WANG, Bo ZHENG, Yueqiang SHANG. Parallel Finite Element Algorithms Based on Two-grid Discretizations for the Steady Navier-Stokes Equations with Damping Term [J]. Chinese Journal of Computational Physics, 2023, 40(5): 535-547. |
| [9] | Jingkun XU, Weihua WANG. Hybrid Simulation of Non-resonant Fishbone Instabilities Excited by Passing Energetic Particles in EAST Tokamak [J]. Chinese Journal of Computational Physics, 2023, 40(3): 291-300. |
| [10] | Hongbo CAI, Yupei XU, Peilin YAO, Enhao ZHANG, Hanxiao HUANG, Shaoping ZHU, Xiantu HE. Hybrid Fluid-PIC Modeling and Its Application in Laser Fusion [J]. Chinese Journal of Computational Physics, 2023, 40(2): 159-168. |
| [11] | Zhanhuang WANG, Bo ZHENG, Yueqiang SHANG. Parallel Two-level Stabilized Finite Element Algorithms for Unsteady Navier-Stokes Equations [J]. Chinese Journal of Computational Physics, 2023, 40(1): 14-28. |
| [12] | Hua ZHANG, Minghui YANG. Stability Analysis of Compressible Viscous Circular Jet [J]. Chinese Journal of Computational Physics, 2022, 39(5): 529-536. |
| [13] | Lihong TANG, Zongmei HE, Yanli YAO. Magnetic Induction HR Neuron with Hidden Extreme Multistability and Its Circuit Implementation [J]. Chinese Journal of Computational Physics, 2022, 39(5): 589-597. |
| [14] | Jiali ZHU, Yueqiang SHANG. A Parallel Two-level Stablized Finite Element Algorithm for Incompressible Flows [J]. Chinese Journal of Computational Physics, 2022, 39(3): 309-317. |
| [15] | Chuang XUE, Xingdong LI, Wenjun SUN, Wenhua YE, Xianjue PENG. A Multi-material Five-equation-reduced Model and Artificial Compression Method for Interface Capture [J]. Chinese Journal of Computational Physics, 2021, 38(3): 257-268. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © Chinese Journal of Computational Physics
E-mail: jswl@iapcm.ac.cn
Supported by Beijing Magtech Co., Ltd.
