Chinese Journal of Computational Physics ›› 2024, Vol. 41 ›› Issue (4): 418-425.DOI: 10.19596/j.cnki.1001-246x.8731
Previous Articles Next Articles
Yali WANG( ), Bo ZHENG, Yueqiang SHANG(
), Bo ZHENG, Yueqiang SHANG( )
)
Received:2023-03-20
Online:2024-07-25
Published:2024-08-24
Contact:
Yueqiang SHANG
CLC Number:
Yali WANG, Bo ZHENG, Yueqiang SHANG. Two-level Grad-div Stabilized Finite Element Methods for Steady Incompressible Navier-Stokes Equations[J]. Chinese Journal of Computational Physics, 2024, 41(4): 418-425.
Add to citation manager EndNote|Ris|BibTeX
URL: http://www.cjcp.org.cn/EN/10.19596/j.cnki.1001-246x.8731
| 算法 | 1/h | 1/H | CPU/s | ‖▽(u-uh)‖0 | ‖p-ph‖0 | 速度收敛阶 | 压力收敛阶 |
| 单水平算法 | 8 | 0.077 | 1.364 7×10-1 | 2.468 2×10-2 | |||
| 27 | 0.715 | 3.977 0×10-3 | 2.031 3×10-3 | 2.906 64 | 2.053 12 | ||
| 64 | 3.071 | 3.025 5×10-4 | 3.596 1×10-4 | 2.984 79 | 2.006 16 | ||
| 125 | 14.536 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 16 | 2.001 27 | ||
| 标准算法 | 8 | 4 | 0.181 | 9.069 4×10-1 | 2.497 8×10-2 | ||
| 27 | 9 | 0.305 | 2.424 1×10-2 | 2.031 3×10-3 | 2.977 67 | 2.062 92 | |
| 64 | 16 | 1.65 | 1.832 2×10-3 | 3.596 1×10-4 | 2.992 35 | 2.006 15 | |
| 125 | 25 | 7.258 | 2.465 5×10-4 | 9.419 0×10-5 | 2.996 12 | 2.001 27 | |
| 算法1 | 8 | 4 | 0.063 | 1.521 3×10-1 | 2.471 8×10-2 | ||
| 27 | 9 | 0.296 | 3.978 5×10-3 | 2.031 3×10-3 | 2.995 61 | 2.054 31 | |
| 64 | 16 | 1.664 | 3.025 6×10-4 | 3.596 1×10-4 | 2.985 23 | 2.006 16 | |
| 125 | 25 | 7.494 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 17 | 2.001 27 | |
| 算法2 | 8 | 4 | 0.065 | 1.510 8×10-1 | 2.471 4×10-2 | ||
| 27 | 9 | 0.319 | 3.978 1×10-3 | 2.031 3×10-3 | 2.989 99 | 2.05417 | |
| 64 | 16 | 1.811 | 3.025 6×10-4 | 3.596 1×10-4 | 2.985 13 | 2.00616 | |
| 125 | 25 | 8.058 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 17 | 2.00127 | |
| 算法3 | 8 | 4 | 0.062 | 1.364 4×10-1 | 2.468 3×10-2 | ||
| 27 | 9 | 0.29 | 3.977 0×10-3 | 2.031 3×10-3 | 2.906 42 | 2.053 15 | |
| 64 | 16 | 1.62 | 3.025 5×10-4 | 3.596 1×10-4 | 2.984 79 | 2.006 16 | |
| 125 | 25 | 7.275 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 16 | 2.001 27 |
Table 1 Errors of approximate solutions by one-level algorithm, standard algorithm and algorithm 1 to algorithm 3
| 算法 | 1/h | 1/H | CPU/s | ‖▽(u-uh)‖0 | ‖p-ph‖0 | 速度收敛阶 | 压力收敛阶 |
| 单水平算法 | 8 | 0.077 | 1.364 7×10-1 | 2.468 2×10-2 | |||
| 27 | 0.715 | 3.977 0×10-3 | 2.031 3×10-3 | 2.906 64 | 2.053 12 | ||
| 64 | 3.071 | 3.025 5×10-4 | 3.596 1×10-4 | 2.984 79 | 2.006 16 | ||
| 125 | 14.536 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 16 | 2.001 27 | ||
| 标准算法 | 8 | 4 | 0.181 | 9.069 4×10-1 | 2.497 8×10-2 | ||
| 27 | 9 | 0.305 | 2.424 1×10-2 | 2.031 3×10-3 | 2.977 67 | 2.062 92 | |
| 64 | 16 | 1.65 | 1.832 2×10-3 | 3.596 1×10-4 | 2.992 35 | 2.006 15 | |
| 125 | 25 | 7.258 | 2.465 5×10-4 | 9.419 0×10-5 | 2.996 12 | 2.001 27 | |
| 算法1 | 8 | 4 | 0.063 | 1.521 3×10-1 | 2.471 8×10-2 | ||
| 27 | 9 | 0.296 | 3.978 5×10-3 | 2.031 3×10-3 | 2.995 61 | 2.054 31 | |
| 64 | 16 | 1.664 | 3.025 6×10-4 | 3.596 1×10-4 | 2.985 23 | 2.006 16 | |
| 125 | 25 | 7.494 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 17 | 2.001 27 | |
| 算法2 | 8 | 4 | 0.065 | 1.510 8×10-1 | 2.471 4×10-2 | ||
| 27 | 9 | 0.319 | 3.978 1×10-3 | 2.031 3×10-3 | 2.989 99 | 2.05417 | |
| 64 | 16 | 1.811 | 3.025 6×10-4 | 3.596 1×10-4 | 2.985 13 | 2.00616 | |
| 125 | 25 | 8.058 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 17 | 2.00127 | |
| 算法3 | 8 | 4 | 0.062 | 1.364 4×10-1 | 2.468 3×10-2 | ||
| 27 | 9 | 0.29 | 3.977 0×10-3 | 2.031 3×10-3 | 2.906 42 | 2.053 15 | |
| 64 | 16 | 1.62 | 3.025 5×10-4 | 3.596 1×10-4 | 2.984 79 | 2.006 16 | |
| 125 | 25 | 7.275 | 4.071 3×10-5 | 9.419 0×10-5 | 2.996 16 | 2.001 27 |
| 算法 | ν | CPU/s | ‖▽(u-uh)‖0 | ‖p-ph‖0 |
| 算法1 | 1 | 7.276 | 2.246 1×10-6 | 9.419 0×10-5 |
| 10-1 | 7.319 | 1.268 4×10-5 | 9.419 0×10-5 | |
| 10-2 | 7.494 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 10-3 | 7.466 | 3.394 0×10-4 | 9.419 0×10-5 | |
| 10-4 | 8.023 | 5.379 9×10-3 | 9.419 4×10-5 | |
| 算法2 | 1 | 7.846 | 2.246 1×10-6 | 9.419 0×10-5 |
| 10-1 | 7.855 | 1.268 4×10-5 | 9.419 0×10-5 | |
| 10-2 | 8.058 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 10-3 | 8.043 | 3.394 0×10-4 | 9.419 0×10-5 | |
| 10-4 | 8.599 | 5.260 0×10-3 | 9.419 4×10-5 | |
| 算法3 | 1 | 7.247 | 2.246 1×10-6 | 9.419 0×10-5 |
| 10-1 | 7.085 | 1.268 4×10-5 | 9.419 0×10-5 | |
| 10-2 | 7.275 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 10-3 | 7.22 | 3.390 9×10-4 | 9.419 0×10-5 | |
| 10-4 | 7.778 | 3.177 4×10-3 | 9.419 0×10-5 |
Table 2 Numerical results of algorithm 1 to algorithm 3 with different viscosity
| 算法 | ν | CPU/s | ‖▽(u-uh)‖0 | ‖p-ph‖0 |
| 算法1 | 1 | 7.276 | 2.246 1×10-6 | 9.419 0×10-5 |
| 10-1 | 7.319 | 1.268 4×10-5 | 9.419 0×10-5 | |
| 10-2 | 7.494 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 10-3 | 7.466 | 3.394 0×10-4 | 9.419 0×10-5 | |
| 10-4 | 8.023 | 5.379 9×10-3 | 9.419 4×10-5 | |
| 算法2 | 1 | 7.846 | 2.246 1×10-6 | 9.419 0×10-5 |
| 10-1 | 7.855 | 1.268 4×10-5 | 9.419 0×10-5 | |
| 10-2 | 8.058 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 10-3 | 8.043 | 3.394 0×10-4 | 9.419 0×10-5 | |
| 10-4 | 8.599 | 5.260 0×10-3 | 9.419 4×10-5 | |
| 算法3 | 1 | 7.247 | 2.246 1×10-6 | 9.419 0×10-5 |
| 10-1 | 7.085 | 1.268 4×10-5 | 9.419 0×10-5 | |
| 10-2 | 7.275 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 10-3 | 7.22 | 3.390 9×10-4 | 9.419 0×10-5 | |
| 10-4 | 7.778 | 3.177 4×10-3 | 9.419 0×10-5 |
| 算法 | α | CPU/s | ‖▽(u-uh)‖0 | ‖p-ph‖0 |
| 算法2 | 0 | 7.258 | 2.465 5×10-4 | 9.419 0×10-5 |
| 10-2 | 7.296 | 1.268 4×10-4 | 9.419 0×10-5 | |
| 10-1 | 7.275 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 1 | 7.186 | 3.390 9×10-5 | 9.419 0×10-5 | |
| 10 | 7.247 | 3.177 4×10-5 | 9.419 0×10-5 |
Table 3 Numerical results of algorithm 2 with different stabilization parameters
| 算法 | α | CPU/s | ‖▽(u-uh)‖0 | ‖p-ph‖0 |
| 算法2 | 0 | 7.258 | 2.465 5×10-4 | 9.419 0×10-5 |
| 10-2 | 7.296 | 1.268 4×10-4 | 9.419 0×10-5 | |
| 10-1 | 7.275 | 4.071 3×10-5 | 9.419 0×10-5 | |
| 1 | 7.186 | 3.390 9×10-5 | 9.419 0×10-5 | |
| 10 | 7.247 | 3.177 4×10-5 | 9.419 0×10-5 |
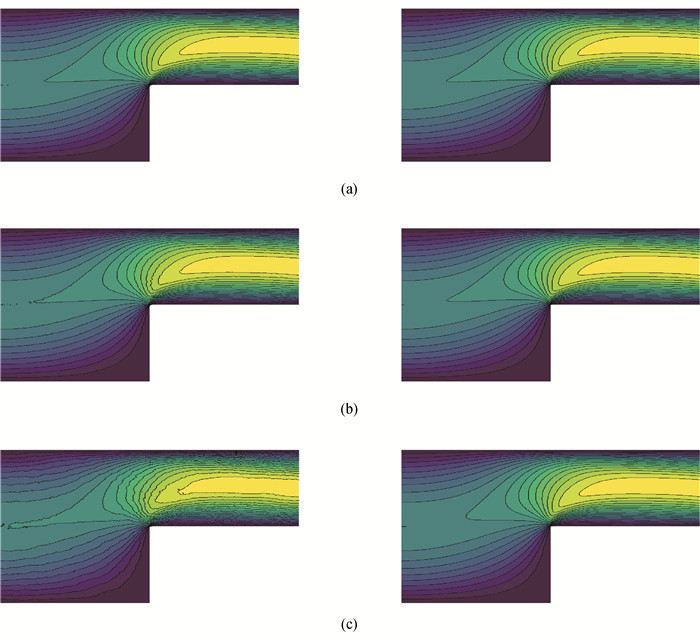
Fig.1 Computed u1 by the standard two-level finite element algorithm (left) and algorithm 2 (right) with different values of ω (a) ω=10; (b) ω=102; (c) ω=103
| 1 |
XU Jinchao . A novel two-grid method for semilinear elliptic equations[J]. SIAM Journal on Scientific Computing, 1994, 15 (1): 231- 237.
DOI |
| 2 |
XU Jinchao . Two-grid discretization techniques for linear and nonlinear PDEs[J]. SIAM Journal on Numerical Analysis, 1996, 33 (5): 1759- 1777.
DOI |
| 3 | LAYTON W . A two-level discretization method for the Navier-Stokes equations[J]. Computers & Mathematics With Applications, 1993, 26 (2): 33- 38. |
| 4 |
HE Yinnian , LI Kaitai . Two-level stabilized finite element methods for the steady Navier-Stokes problem[J]. Computing, 2005, 74 (4): 337- 351.
DOI |
| 5 | LI Jian , HE Yinnian , XU Hui . A multi-level stabilized finite element method for the stationary Navier-Stokes equations[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196 (29/30): 2852- 2862. |
| 6 |
WEN Juan , HUANG Pengzhan , HE Yaling . The two-level stabilized finite element method based on multiscale enrichment for the stokes eigenvalue problem[J]. Acta Mathematica Scientia, 2021, 41 (2): 381- 396.
DOI |
| 7 | HE Yinnian , WANG Aiwen . A simplified two-level method for the steady Navier-Stokes equations[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197 (17/18): 1568- 1576. |
| 8 | OLSHANSKII M A , REUSKEN A . Grad-div stablilization for stokes equations[J]. Mathematics of Computation, 2004, 73 (248): 1699- 1718. |
| 9 |
DE FRUTOS J , GARCÍA-ARCHILLA B , JOHN V , et al. Analysis of the grad-div stabilization for the time-dependent Navier-Stokes equations with inf-sup stable finite elements[J]. Advances in Computational Mathematics, 2018, 44 (1): 195- 225.
DOI |
| 10 |
AHMED N . On the grad-div stabilization for the steady Oseen and Navier-Stokes equations[J]. Calcolo, 2017, 54 (1): 471- 501.
DOI |
| 11 | 王湛煌, 郑波, 尚月强. 非定常Navier-Stokes方程的并行两水平稳定有限元算法[J]. 计算物理, 2023, 40 (1): 14- 28. |
| 12 | 朱家莉, 尚月强. 不可压缩流的并行两水平稳定有限元算法[J]. 计算物理, 2022, 39 (3): 309- 317. |
| 13 | 丁琪, 尚月强. 非定常Navier-Stokes方程基于两重网格离散的有限元并行算法[J]. 计算物理, 2020, 37 (1): 10- 18. |
| 14 |
LI Wei , HUANG Pengzhan , HE Yinnian . Grad-div stabilized finite element schemes for the fluid-fluid interaction model[J]. Communications in Computational Physics, 2021, 30 (2): 536- 566.
DOI |
| 15 | LAYTON W , XU Shuxian . Stability in 3d of a sparse grad-div approximation of the Navier-Stokes equations[J]. Journal of Mathematical Analysis and Applications, 2022, 516 (1): 126484. |
| 16 | ADAMS R A . Sobolev spaces[M]. New York: Academaic Press, 1975. |
| 17 | SHANG Yueqiang . A two-level subgrid stabilized Oseen iterative method for the steady Navier-Stokes equations[J]. Journal of Computational Physics, 2013, 233, 210- 226. |
| 18 | JOHN V . Finite element methods for incompressible flow problems[M]. Cham: Springer Cham, 2016. |
| 19 | HECHT F . New development in freefem++[J]. Journal of Numerical Mathematics, 2012, 20 (3/4): 251- 265. |
| 20 | HE Yinnian , LI Jian . Convergence of three iterative methods based on the finite element discretization for the stationary Navier-Stokes equations[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198 (15/16): 1351- 1359. |
| [1] | Hexiao FAN, Xingding CHEN. A Class of Preconditioners for Static Elastic Crack Problems Modeled by Extended Finite Element Method [J]. Chinese Journal of Computational Physics, 2024, 41(2): 151-160. |
| [2] | Puyang GAO. Non-isothermal Polymer Filling Process via Phase Field Method in Three Dimensions [J]. Chinese Journal of Computational Physics, 2023, 40(6): 689-698. |
| [3] | Shaoliang HU, Kailong XU, Ran XU, Zaigang LIU, Xiaowen XU, Hengbin AN, Ronghong FAN, Zhenyu WANG, Wei WANG. A Algebraic Multigrid Algorithm Based on Hybrid Coarsening for Pressure Poisson Equation [J]. Chinese Journal of Computational Physics, 2023, 40(5): 527-534. |
| [4] | Guoliang WANG, Bo ZHENG, Yueqiang SHANG. Parallel Finite Element Algorithms Based on Two-grid Discretizations for the Steady Navier-Stokes Equations with Damping Term [J]. Chinese Journal of Computational Physics, 2023, 40(5): 535-547. |
| [5] | Zhanhuang WANG, Bo ZHENG, Yueqiang SHANG. Parallel Two-level Stabilized Finite Element Algorithms for Unsteady Navier-Stokes Equations [J]. Chinese Journal of Computational Physics, 2023, 40(1): 14-28. |
| [6] | Jiali ZHU, Yueqiang SHANG. A Parallel Two-level Stablized Finite Element Algorithm for Incompressible Flows [J]. Chinese Journal of Computational Physics, 2022, 39(3): 309-317. |
| [7] | HU Jun, LIU Quan, NI Guoxi. Bayesian Sparse Identification of Time-varying Partial Differential Equations [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2021, 38(1): 25-34. |
| [8] | LI Xindong, ZHAO Yingkui, HU Zongmin, JIANG Zonglin. Investigation of Normal Shock Structure by Using Navier-Stokes Equations with the Second Viscosity [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(5): 505-513. |
| [9] | DING Qi, SHANG Yueqiang. Parallel Finite Element Algorithms Based on Two-grid Discretization for Time-dependent Navier-Stokes Equations [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(1): 10-18. |
| [10] | ZHANG Qingfu, YAO Jun, HUANG Zhaoqin, LI Yang, WANG Yueying. A Multiscale Deep Learning Model for Fractured Porous Media [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(6): 665-672. |
| [11] | WEN Xiaojing, QU Yu, CHEN Chengzhao. Numerical Study of Circular Dichroism Generated by Bilayered Split Rings [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(3): 357-362. |
| [12] | CHEN Gong, WANG Yizheng, WANG Ye, ZHANG Chunyu. Reduced Basis Finite Element Method for Fast Solution of Parameterized Partial Differential Equations [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(5): 515-524. |
| [13] | YU Chenyang, FAN Xuanhua, WANG Keying, XIAO Shifu. Parallel Computing of Multipoint-Base-Excited Harmonic Response with PANDA Platform [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(4): 443-450. |
| [14] | GE Zhihao, WU Huili. A Penalized Finite Element Method of Nonlocal Diffusion Problem with Volume Constraints [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(2): 161-168. |
| [15] | TANG Qiuming, ZHEN Tianyi, LI Danyun, GAO Qiang. Mechanical Properties of Graphene/Hydroxyapatite Composite Materials: Numerical Study [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(1): 71-76. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
Copyright © Chinese Journal of Computational Physics
E-mail: jswl@iapcm.ac.cn
Supported by Beijing Magtech Co., Ltd.
