Solution of Wigner-Poisson System with Combining Flux Balance and Fourier Spectrum Methods

doi:10.19596/j.cnki.1001-246x.8613

Abstract

Abstract:

The difference between quantum plasma and classical plasma is mainly reflected in the following two aspects: 1) the statistical equilibrium state of the system changes from the classical Maxwell distribution to the Fermi-Dirac distribution; 2) the single-particle quantum wave effect of electrons cannot be avoided. Corresponding to the Vlasov equation in the classical plasma, the kinetic equation of the quantum plasma is the Wigner equation, but the numerical solution of the Wigner equation is more complicated than the Vlasov equation. In this paper, we propose a new method based on flux balance and Fourier spectrum methods. The hybrid method is used to solve the Wigner-Poisson equations. This method adopts different time advancing algorithms in the coordinate and velocity spaces. Compared with the general discrete Euler method, it can significantly improve the accuracy of nonlinear simulation results. This paper investigates the behavioral changes of some common electrostatic kinetic instabilities in quantum plasmas through this method; verifies the reliability of the code through linear eigensolutions, and then simulates some nonlinear phenomena, including Nonlinear Landau damping and nonlinear saturation for two-stream instability, etc.

Key words: quantum plasmas, kinetic, Euler method, nonlinear effects

Tianxing HU, Zhengmao SHENG, Dong WU. Solution of Wigner-Poisson System with Combining Flux Balance and Fourier Spectrum Methods[J]. Chinese Journal of Computational Physics, 2023, 40(2): 248-257.

Figures/Tables 9

Fig.1 Comparison of pure Fourier method and Hybrid method (a) two-stream instability; (b) energy conservation

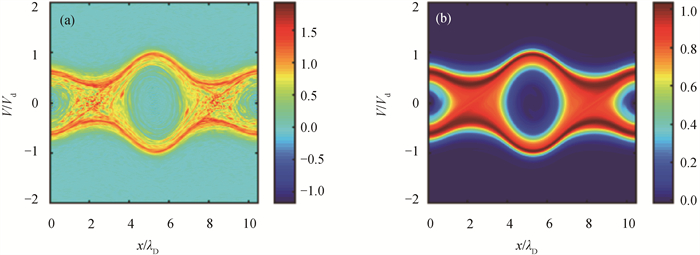
Fig.2 Comparison of pure Fourier method and Hybrid method of a classical BGK equilibrium (a)FSM($ t=187 \omega_{\mathrm{p}}^{-1}$); (b)Hybrid($t=187 \omega_{\mathrm{p}}^{-1} $)

Fig.3 Demonstration of recurrence (a) Landau damping without hyper-collision; (b) without hyper-collision

Fig.4 Comparison of eigen-value solution and linear simulation of (a) Landau damping and (b) two-stream instability

Fig.5 Quantum Landau damping with varying Q

Fig.6 Quantum Landau damping with varying Θ

Fig.7 Comparison of the eigen-value solution and the numerical solution of two-stream instability

Fig.8 Numerical results of nonlinear Landau damping: classical and quantum mechanical.

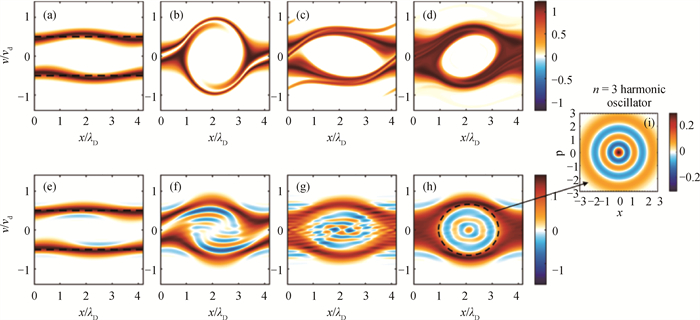
Fig.9 Comparison of classical and quantum BGK equilibrium (a) t=48ωp-1; (b) t=55ωp-1; (c) t=80ωp-1; (d) t=316ωp-1; (e) t=48ωp-1; (f) t=55ωp-1; (g) t=80ωp-1; (h) t=316ωp-1

References 28

1	贺贤土. 等离子体中集体效应对韧致辐射的影响[J]. 物理学报, 1981, 30 (11): 1415- 1422.
2	贺贤土. 激励Brillouin散射非线性致稳过程的阻尼效应[J]. 物理学报, 1982, 31 (7): 882- 894. DOI
3	贺贤土. 等离子体中大幅波与低频振荡粒子非线性相互作用效应[J]. 物理学报, 1982, 31 (10): 1317- 1336.
4	贺贤土. 高频波激发低频磁场和离子声波的重整化强湍动理论[J]. 物理学报, 1986, 35 (3): 283- 299.
5	贺贤土. 等离子体中粒子与cavitons相互作用[J]. 物理学报, 1987, 36 (2): 199- 207. DOI
6	ZHU S P , HE X T , ZHENG C . Slow-time-scale magnetic fields driven by fast-time-scale waves in an underdense relativistic Vlasov plasma[J]. Physics of Plasmas, 2001, 8 (1): 321- 328. DOI
7	ZHU S P , ZHENG C Y , HE X T . A theoretical model for a spontaneous magnetic field in intense laser plasma interaction[J]. Physics of Plasmas, 2003, 10 (10): 4166- 4168. DOI
8	HE X , LI J , FAN Z , et al. A hybrid-drive nonisobaric-ignition scheme for inertial confinement fusion[J]. Physics of Plasmas, 2016, 23 (8): 082706. DOI
9	ZHANG J , WANG W , YANG X , et al. Double-cone ignition scheme for inertial confinement fusion[J]. Philosophical Transactions of the Royal Society A, 2020, 378 (2184): 20200015. DOI
10	DORNHEIM T , GROTH S , BONITZ M . The uniform electron gas at warm dense matter conditions[J]. Physics Reports, 2018, 744, 1- 86. DOI
11	MANFREDI G , HERVIEUX P A , HURST J . Phase-space modeling of solid-state plasmas[J]. Reviews of Modern Plasma Physics, 2019, 3 (1): 1- 55. DOI
12	CAI H B , YAN X X , YAO P L , et al. Hybrid fluid-particle modeling of shock-driven hydrodynamic instabilities in a plasma[J]. Matter and Radiation at Extremes, 2021, 6 (3): 035901. DOI
13	WU D , YU W , FRITZSCHE S , et al. Particle-in-cell simulation method for macroscopic degenerate plasmas[J]. Physical Review E, 2020, 102 (3): 033312. DOI
14	BONITZ M . Quantum kinetic theory[M]. Berlin: Springer, 2016.
15	LIANG J H , HU T X , WU D , et al. Kinetic study of quantum two-stream instability by Wigner approach[J]. Physical Review E, 2021, 103 (3): 033207. DOI
16	SUH N-D , FEIX M R , BERTRAND P . Numerical simulation of the quantum Liouville-Poisson system[J]. Journal of Computational Physics, 1991, 94 (2): 403- 418. DOI
17	WIGNER E . On the quantum correction for thermodynamic equilibrium[J]. Physical Review, 1932, 40 (5): 749- 759. DOI
18	KADANOFF L , BAYM G . Quantum statistical mechanics[M]. New York: W A Benjamin Inc, 1962.
19	CHENG C Z , KNORR G . The integration of the Vlasov equation in configuration space[J]. Journal of Computational Physics, 1976, 22 (3): 330- 351. DOI
20	STRANG G . On the construction and comparison of difference schemes[J]. SIAM Journal on Numerical Analysis, 1968, 5 (3): 506- 517. DOI
21	FILBET F , SONNENDRÜCKER E , BERTRAND P . Conservative numerical schemes for the Vlasov equation[J]. Journal of Computational Physics, 2001, 172 (1): 166- 187. DOI
22	BERNSTEIN I B , GREENE J M , KRUSKAL M D . Exact nonlinear plasma oscillations[J]. Physical Review, 1957, 108 (3): 546- 550. DOI
23	ZAKHAROV V E . Collapse of Langmuir waves[J]. Sov Phys JETP, 1972, 35 (5): 908- 914.
24	DANNERT T , JENKO F . Vlasov simulation of kinetic shear Alfvén waves[J]. Computer Physics Communications, 2004, 163 (2): 67- 78. DOI
25	MANFREDI G , HAAS F . Self-consistent fluid model for a quantum electron gas[J]. Physical Review B, 2001, 64 (7): 075316. DOI
26	HAAS F , MANFREDI G , FEIX M . Multistream model for quantum plasmas[J]. Physical Review E, 2000, 62 (2): 2763. DOI
27	MANFREDI G . How to model quantum plasmas[J]. Fields Inst Commun, 2005, 46, 263- 287.
28	DALIGAULT J . On the quantum Landau collision operator and electron collisions in dense plasmas[J]. Physics of Plasmas, 2016, 23 (3): 032706.

[1]	Wenjing MA, Jin WANG, Hui GUO, Meini LYU, Hongze ZHANG, Dongde LI. Phase Field Crystal Method Study on Inhibitory Mechanism of the Growth of Kirkendall Voids During Deformation Process at the Interface of Metal Micro Interconnect Structures [J]. Chinese Journal of Computational Physics, 2023, 40(4): 416-424.
[2]	Yuanzhi ZHOU, Chunyang ZHENG, Zhanjun LIU, Lihua CAO, Ruijin CHENG, Xiantu HE. Suppression of Stimulated Raman Scattering and Stimulated Brillouin Scattering in Weakly Magnetized Plasmas [J]. Chinese Journal of Computational Physics, 2023, 40(2): 136-146.
[3]	Wenshuai ZHANG, Hongbo CAI, Enhao ZHANG, Bao DU, Shiyang ZOU, Shaoping ZHU. Influence of Mach Number on Structure of Collisional Plasma Shock Waves: Fully Kinetic Simulations [J]. Chinese Journal of Computational Physics, 2023, 40(2): 199-209.
[4]	Jin WANG, Wen-jing MA, Yu-zhou LIU, Mei-ni LÜ, Kai-jing ZHANG. Morphological Evolution and Growth Kinetics in Primary Crystallization of Amorphous: Phase Field Method [J]. Chinese Journal of Computational Physics, 2022, 39(4): 403-410.
[5]	LI Kang, LI Shouxian, LIU Na. High-precision Numerical Simulation of Strong Explosion Fireball with Adaptive Mesh [J]. Chinese Journal of Computational Physics, 2021, 38(2): 146-152.
[6]	ZOU Xing, CHEN Songze, GUO Zhaoli. A Well-balanced Gas Kinetic Scheme [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2020, 37(6): 653-666.
[7]	ZENG Wei, CHEN Songze, GUO Zhaoli. Feasibility of Simulation on Flow in Porous Media with Gas Kinetic Scheme [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2019, 36(5): 551-558.
[8]	CHEN Bin, LIU Ge. Anslysis of Kinetic Energy Dissipation Rate and POD Reconstruction of a Channel Flow [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(2): 169-177.
[9]	PENG Gang. Calculation of Kinetic Parameters with Continuous Energy Adjoint Weighted Monte Carlo Method [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2018, 35(1): 87-94.
[10]	WANG Lu, XU Jiangrong, LIU Baoyin. A Field-Equation Turbulence Model Closed By Lagrange Method [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2016, 33(3): 305-310.
[11]	ZHEN Yaxin, NI Guoxi. Adaptive Moving Mesh Kinetic Scheme for Reactive Fluids [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2015, 32(6): 677-684.
[12]	XU Xihua, NI Guoxi. A High-order Moving Mesh Kinetic Scheme Based on WENO Reconstruction for Compressible Flows [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2013, 30(4): 509-514.
[13]	WU Junlin, LI Zhihui, JIANG Xinyu. One-dimensional Shock-tube and Two-dimensional Plate Flows in Boltzmann-Rykov Model Involving Rotational Energy [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2013, 30(3): 326-336.
[14]	GAN Wenbiao, ZHOU Zhou. Reynolds-averaged Navier-Stokes Method with Laminar Kinetic Energy Turbulent Model [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2013, 30(2): 169-179.
[15]	YANG Xiquan, TANG Gang, HAN Kui, XIA Hui, HAO Dapeng, XUN Zhipeng, ZHOU Wei, WEN Rongji, CHEN Yuling, WANG Juan. Numerical Study on Roughness Distributions of 1+1 Dimensional Noisy Kuramoto-Sivashinsky Equation [J]. CHINESE JOURNAL OF COMPUTATIONAL PHYSICS, 2011, 28(1): 125-130.