计算物理 ›› 2024, Vol. 41 ›› Issue (1): 64-74.DOI: 10.19596/j.cnki.1001-246x.8787
• 面向超级计算机的性能优化技术与数值并行算法专刊 • 上一篇 下一篇
徐小文1,2( ), 莫则尧1,2, 胡少亮1,2, 安恒斌1,2
), 莫则尧1,2, 胡少亮1,2, 安恒斌1,2
收稿日期:2023-06-30
出版日期:2024-01-25
发布日期:2024-02-05
作者简介:徐小文, 男, 博士, 研究员, 博士生导师, 研究方向为大规模并行计算与并行算法, E-mail: xwxu@iapcm.ac.cn
基金资助:
Xiaowen XU1,2( ), Zeyao MO1,2, Shaoliang HU1,2, Hengbin AN1,2
), Zeyao MO1,2, Shaoliang HU1,2, Hengbin AN1,2
Received:2023-06-30
Online:2024-01-25
Published:2024-02-05
摘要:
针对实际应用中稀疏线性解法器计算复杂度偏离线性扩展的瓶颈问题, 提出特征修正预条件算法统一框架, 通过凝练物理特征中影响算法效率的代数特征, 结合多层次特征分析, 构造特征修正组件。通过几类典型特征修正预条件算法及应用成效, 展示了该框架的有效性。
中图分类号:
徐小文, 莫则尧, 胡少亮, 安恒斌. 特征修正并行预条件算法框架[J]. 计算物理, 2024, 41(1): 64-74.
Xiaowen XU, Zeyao MO, Shaoliang HU, Hengbin AN. Feature-modified Algorithm Framework for Parallel Preconditioning in Sparse Linear Solvers[J]. Chinese Journal of Computational Physics, 2024, 41(1): 64-74.
| 代数特征 | 内涵 | 特征来源 | 典型应用场景 | |
| 领域 | 示例 | |||
| 分区多尺度性 | 是指线性方程组的系数矩阵具有多尺度性,即:矩阵非对角元素在数值上相差几个、甚至十几个数量级,且多尺度点把整体区域划分为不同尺度的子区域 | 该特征主要由多介质、大变形、多物理耦合与非线性效应等物理特征综合影响所致 | 激光聚变 结构力学 电子学系统 | 左:多尺度点的非对角线元素(S1-S6)相差6个量级; 右:颜色所示的多尺度点将区域划分为不同尺度的子区域 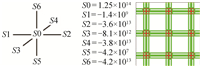 |
| 周期非正定性 | 是指电子学系统仿真中时谐Maxwell方程的周期性导致离散线性方程组具有非正定性质 | 该特征由电磁波传播的周期性所致 | 电子学系统 | 非正定性时谐Maxwell方程: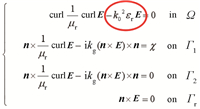 |
| 接触非对称性 | 是指结构力学分析中热-力-接触多物理耦合导致离散线性方程组具有非对称性质 | 该特征由工程力学设计中接触耦合所致 | 结构力学 | 非对称性热-力-接触耦合方程: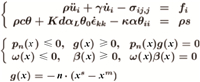 |
| 耦合块结构 | 是指由于多物理耦合导致矩阵特有的块结构 | 该特征由辐射传输中辐射与电子、离子特有的耦合关系所致 | 激光聚变 | 辐射与电子、离子耦合块矩阵: |
| 贯序动态变化 | 是指一次完整模拟需要求解由批量线性方程组构成的方程组序列,且方程组性质动态变化 | 该特征主要由长时间积分和非线性迭代等因素所致 | 激光聚变 结构力学 | 典型多物理应用:数万时间步,每个时间步求解多个非线性系统且需近10次非线性迭代,共需要求解数十万个线性方程组:{Aixi=bi, i=1, …, neq},且Ai的性质动态变化 |
表1 三类典型应用中5类代数特征内涵、来源及典型场景
Table 1 5 kinds of algebraic features in 3 typical applications: Connotations, sources and typical scenarios
| 代数特征 | 内涵 | 特征来源 | 典型应用场景 | |
| 领域 | 示例 | |||
| 分区多尺度性 | 是指线性方程组的系数矩阵具有多尺度性,即:矩阵非对角元素在数值上相差几个、甚至十几个数量级,且多尺度点把整体区域划分为不同尺度的子区域 | 该特征主要由多介质、大变形、多物理耦合与非线性效应等物理特征综合影响所致 | 激光聚变 结构力学 电子学系统 | 左:多尺度点的非对角线元素(S1-S6)相差6个量级; 右:颜色所示的多尺度点将区域划分为不同尺度的子区域 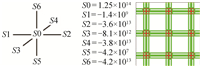 |
| 周期非正定性 | 是指电子学系统仿真中时谐Maxwell方程的周期性导致离散线性方程组具有非正定性质 | 该特征由电磁波传播的周期性所致 | 电子学系统 | 非正定性时谐Maxwell方程: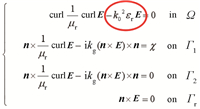 |
| 接触非对称性 | 是指结构力学分析中热-力-接触多物理耦合导致离散线性方程组具有非对称性质 | 该特征由工程力学设计中接触耦合所致 | 结构力学 | 非对称性热-力-接触耦合方程: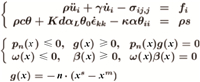 |
| 耦合块结构 | 是指由于多物理耦合导致矩阵特有的块结构 | 该特征由辐射传输中辐射与电子、离子特有的耦合关系所致 | 激光聚变 | 辐射与电子、离子耦合块矩阵: |
| 贯序动态变化 | 是指一次完整模拟需要求解由批量线性方程组构成的方程组序列,且方程组性质动态变化 | 该特征主要由长时间积分和非线性迭代等因素所致 | 激光聚变 结构力学 | 典型多物理应用:数万时间步,每个时间步求解多个非线性系统且需近10次非线性迭代,共需要求解数十万个线性方程组:{Aixi=bi, i=1, …, neq},且Ai的性质动态变化 |
| 代数特征 | 具体影响 | 影响程度 |
| 分区多尺度性 | 相对于单尺度系统,该特征导致传统AMG的光滑和粗化等组件质量下降,收敛速度严重退化 | 算法组件算法参数 |
| 接触非对称性 | 传统AMG算法机理难以适应非对称问题 | 算法机理 |
| 周期非正定性 | 传统AMG算法机理难以适应非正定问题 | 算法机理 |
| 耦合块结构 | 块结构蕴含的耦合关系导致传统AMG的光滑、粗化、插值等组件质量下降,收敛速度退化 | 算法组件算法参数 |
| 贯序动态变化 | 不存在单一算法对所有系统都是线性扩展的,传统AMG算法流程限制了方程组序列动态变化的调优空间 | 算法流程 |
表2 5个代数特征对AMG预条件算法的影响
Table 2 Impacts of 5 algebraic features on the AMG algorithm
| 代数特征 | 具体影响 | 影响程度 |
| 分区多尺度性 | 相对于单尺度系统,该特征导致传统AMG的光滑和粗化等组件质量下降,收敛速度严重退化 | 算法组件算法参数 |
| 接触非对称性 | 传统AMG算法机理难以适应非对称问题 | 算法机理 |
| 周期非正定性 | 传统AMG算法机理难以适应非正定问题 | 算法机理 |
| 耦合块结构 | 块结构蕴含的耦合关系导致传统AMG的光滑、粗化、插值等组件质量下降,收敛速度退化 | 算法组件算法参数 |
| 贯序动态变化 | 不存在单一算法对所有系统都是线性扩展的,传统AMG算法流程限制了方程组序列动态变化的调优空间 | 算法流程 |
| 序号 | 特征修正组件 | 内涵 |
| 1 | 代数界面提取(AI) | 识别并提取多尺度矩阵的关键特征,为解决分区多尺度性导致AMG算法收敛速度变慢的问题提供工具 |
| 2 | 正定预处理(PD) | 构造具有正定性质的预条件矩阵,解决周期非正定性导致AMG算法的组件难以构造的问题 |
| 3 | 对称预处理(Sym) | 构造具有对称性质的预条件矩阵,解决接触非对称性导致AMG算法的组件难以构造的问题 |
| 4 | 物理量粗化(PCTL) | 基于特殊粗化解耦块结构系统,解决耦合块结构导致AMG算法收敛速度变慢的问题 |
| 5 | 自适应启动(aSetup) | 设置算法空间及自适应切换条件,解决贯序动态变化特征导致AMG算法静态策略可扩展性瓶颈 |
表3 针对5个代数特征的特征修正组件
Table 3 Feature modification components for 5 algebraic features
| 序号 | 特征修正组件 | 内涵 |
| 1 | 代数界面提取(AI) | 识别并提取多尺度矩阵的关键特征,为解决分区多尺度性导致AMG算法收敛速度变慢的问题提供工具 |
| 2 | 正定预处理(PD) | 构造具有正定性质的预条件矩阵,解决周期非正定性导致AMG算法的组件难以构造的问题 |
| 3 | 对称预处理(Sym) | 构造具有对称性质的预条件矩阵,解决接触非对称性导致AMG算法的组件难以构造的问题 |
| 4 | 物理量粗化(PCTL) | 基于特殊粗化解耦块结构系统,解决耦合块结构导致AMG算法收敛速度变慢的问题 |
| 5 | 自适应启动(aSetup) | 设置算法空间及自适应切换条件,解决贯序动态变化特征导致AMG算法静态策略可扩展性瓶颈 |
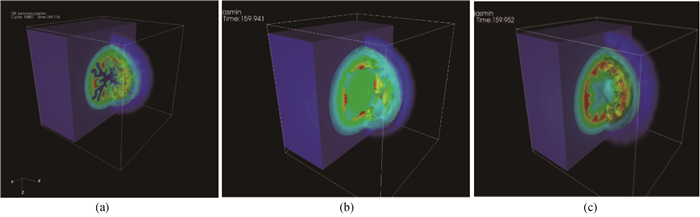
图4 不同建模对内爆流体界面不稳定性模拟的影响 (a)纯流体建模;(b)三温热传导建模;(c)多群扩散建模
Fig.4 Impact of different physical modeling on implosion hydrodynamic instability simulations (a) fluid modeling; (b) three-temperature heat conduction modeling; (c) multi-group diffusion modeling
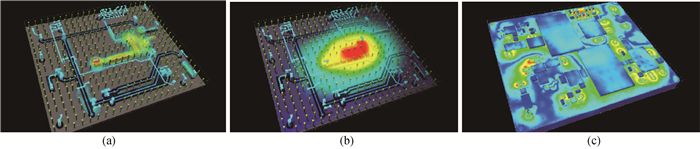
图5 射频前端系统级封装电磁-热-力多物理耦合模拟结果 (a)电磁串扰分析结果; (b)温度分布; (c)应力分布
Fig.5 Simulation results of electromagnetic-thermal-mechanical multiphysics coupling for system in package (SiP) (a) electromagnetic crosstalk analysis; (b) temperature distribution; (c) stress distribution
| 1 |
莫则尧, 张爱清, 曹小林, 等. 多介质辐射流体力学数值模拟中的并行计算研究[J]. 自然科学进展, 2006, 16 (3): 287- 292.
DOI |
| 2 | ANG J, EVANS K, GEIST A, et al. Report on the workshop on extreme-scale solvers: Transition to future architectures[R]. Washington, D. C: Office of Advanced Scientific Computing Research, U.S. Department of Energy, 2012: 8-9. |
| 3 |
ANZT H , BOMAN E , FALGOUT R , et al. Preparing sparse solvers for exascale computing[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2020, 378 (2166): 20190053.
DOI |
| 4 | SAAD Y . Iterative methods for sparse linear systems[M]. 2nd ed Philadelphia: SIAM. |
| 5 | FALGOUT R D, YANG U M. hypre: A library of high performance preconditioners[C]//Computational Science-ICCS 2002. Amsterdam, The Netherlands: Springer, 2002: 632-641. |
| 6 | BALAY S , ABHYANKAR S , ADAMS M , et al. PETSc users manual[M]. Argonne, IL: Argonne National Laboratory, 2019. |
| 7 |
HEROUX M A , BARTLETT R A , HOWLE V E , et al. An overview of the Trilinos project[J]. ACM Transactions on Mathematical Software, 2005, 31 (3): 397- 423.
DOI |
| 8 |
XU Xiaowen , YUE Xiaoqiang , MAO Runzhang , et al. JXPAMG: A parallel algebraic multigrid solver for extreme-scale numerical simulations[J]. CCF Transactions on High Performance Computing, 2023, 5 (1): 72- 83.
DOI |
| 9 |
胡少亮, 徐小文, 安恒斌, 等. 应用特征驱动的并行数值代数解法器JPSOL[J]. 计算物理, 2024, 41 (1): 110- 121.
DOI |
| 10 | TROTTENBERG U , OOSTERLEE C W , SCHULLER A . Multigrid[M]. San Diego: Academic Press, 2000. |
| 11 | 徐小文. 并行代数多重网格算法: 大规模计算应用现状与挑战[J]. 数值计算与计算机应用, 2019, 40 (4): 243- 260. |
| 12 |
XU Xiaowen , MO Zeyao . Algebraic interface-based coarsening AMG preconditioner for multi-scale sparse matrices with applications to radiation hydrodynamics computation[J]. Numerical Linear Algebra With Applications, 2017, 24 (2): e2078.
DOI |
| 13 | 刘笑, 徐小文. 求解多尺度稀疏矩阵的代数界面优先AMG光滑子[J]. 数值计算与计算机应用, 2023, 44 (1): 1- 11. |
| 14 |
胡少亮, 徐小文, 郑宇腾, 等. 系统级封装应用中时谐Maxwell方程大规模计算的求解算法: 现状与挑战[J]. 计算物理, 2021, 38 (2): 131- 145.
DOI |
| 15 |
AN Hengbin , MO Zeyao , WANG Jingtao , et al. Shear decoupled parallel scalable preconditioners for nonlinear Thermo-Mechanical coupled contact applications[J]. Journal of Scientific Computing, 2022, 90, 4.
DOI |
| 16 | 徐小文, 莫则尧, 安恒斌. 求解二维三温辐射扩散方程组的一种代数两层迭代方法[J]. 计算物理, 2009, 26 (1): 1- 8. |
| 17 | 徐小文, 莫则尧, 安恒斌. 求解大规模稀疏线性代数方程组序列的自适应AMG预条件策略[J]. 中国科学(信息科学), 2016, 46 (10): 1411- 1420. |
| 18 |
XU Xiaowen , MO Zeyao , YUE Xiaoqiang , et al. αSetup-AMG: an adaptive-setup-based parallel AMG solver for sequence of sparse linear systems[J]. CCF Transactions on High Performance Computing, 2020, 2 (2): 98- 110.
DOI |
| 19 |
HUANG Silu , YUE Xiaoqiang , XU Xiaowen . αSetup-PCTL: An adaptive setup-based two-level preconditioner for sequence of linear systems of three-temperature energy equations[J]. Communications in Computational Physics, 2022, 32 (5): 1287- 1309.
DOI |
| 20 |
胡少亮, 许开龙, 徐然, 等. 求解压力Poisson方程的混合粗化代数多重网格算法[J]. 计算物理, 2023, 40 (5): 527- 534.
DOI |
| 21 |
舒适, 岳孝强, 何剑萌, 等. 多群辐射扩散问题特征驱动的并行AMG法[J]. 计算物理, 2024, 41 (1): 87- 97.
DOI |
| 22 |
冯春生, 李仕哲, 刘生豪, 等. 面向渗流力学应用特征的预条件方法[J]. 计算物理, 2024, 41 (1): 98- 109.
DOI |
| 23 |
安恒斌, 莫则尧. 辐射扩散方程的非线性迭代方法[J]. 计算物理, 2024, 41 (1): 75- 86.
DOI |
| 24 |
郝悦, 黄思路, 徐小文. 三温能量方程离散线性系统的两层迭代算法收敛因子估计及特征分析[J]. 计算物理, 2024, 41 (1): 122- 130.
DOI |
| 25 | 徐小文. 可扩展并行预条件迭代方法研究验收报告: 2017YFB0202103[R]. [S. l.:s. n.], 2021. |
| 26 | TIAN Rong , ZHOU Mozhen , WANG Jingtao , et al. A challenging dam structural analysis: large-scale implicit thermo-mechanical coupled contact simulation on Tianhe-Ⅱ[J]. Computational Mechanics, 2019, 63 (1): 99- 119. |
| 27 | 邹海峰. 基于图神经网络的稀疏线性代数方程组智能迭代算法研究[D]. 北京: 中国工程物理研究院研究生院, 2023. |
| 28 | ZOU Haifeng, XU Xiaowen, ZHANG Chensong, et al. AutoAMG(θ): An auto-tuned AMG method based on deep learning for strong threshold[EB/OL]. (2023-08-16)[2023-06-10]. https://doi.org/10.48550/arXiv.2307.09879. |
| [1] | 刘杰, 石永振, 杨博, 张翔, 陈新海, 张华健, 郭晓威, 李胜国, 李润华, 彭晋韬, 肖调杰, 陈旭光, 张庆阳, 李彪, 冷灿, 李翊谁, 王庆林. 天河超算系统并行算法库[J]. 计算物理, 2024, 41(1): 9-21. |
| [2] | 胡少亮, 徐小文, 安恒斌, 徐然, 范荣红. 应用特征驱动的并行数值代数解法器JPSOL[J]. 计算物理, 2024, 41(1): 110-121. |
| [3] | 郝悦, 黄思路, 徐小文. 三温能量方程离散线性系统的两层迭代算法收敛因子估计及特征分析[J]. 计算物理, 2024, 41(1): 122-130. |
| [4] | 王国梁, 郑波, 尚月强. 带阻尼项定常Navier-Stokes方程的并行两水平有限元算法[J]. 计算物理, 2023, 40(5): 535-547. |
| [5] | 胡毅, 安恒斌. 半导体器件数值模拟中电子连续性方程的求解算法[J]. 计算物理, 2023, 40(5): 570-582. |
| [6] | 王湛煌, 郑波, 尚月强. 非定常Navier-Stokes方程的并行两水平稳定有限元算法[J]. 计算物理, 2023, 40(1): 14-28. |
| [7] | 胡晓燕, 范征锋. 惯性约束聚变内爆中基于多块结构网格的高效辐射扩散并行算法[J]. 计算物理, 2022, 39(3): 277-285. |
| [8] | 朱家莉, 尚月强. 不可压缩流的并行两水平稳定有限元算法[J]. 计算物理, 2022, 39(3): 309-317. |
| [9] | 蔡颖, 张存波, 刘旭, 范征锋, 刘元元, 徐小文, 张爱清. 二维球坐标系中子输运方程的一种并行SN算法[J]. 计算物理, 2022, 39(2): 143-152. |
| [10] | 胡少亮, 徐小文, 郑宇腾, 赵振国, 王卫杰, 徐然, 安恒斌, 莫则尧. 系统级封装应用中时谐Maxwell方程大规模计算的求解算法:现状与挑战[J]. 计算物理, 2021, 38(2): 131-145. |
| [11] | 丁琪, 尚月强. 非定常Navier-Stokes方程基于两重网格离散的有限元并行算法[J]. 计算物理, 2020, 37(1): 10-18. |
| [12] | 张守慧, 梁栋. 二维抛物型问题的Strang型交替分段区域分裂格式[J]. 计算物理, 2018, 35(4): 413-428. |
| [13] | 祁美玲, 杨琼, 王苍龙, 田园, 杨磊. 结构材料辐照损伤的分子动力学程序GPU并行化及优化[J]. 计算物理, 2017, 34(4): 461-467. |
| [14] | 李超龙, 石海泉, 吕建钦. 双圆筒加速透镜中强流束传输的模拟[J]. 计算物理, 2013, 30(3): 403-408. |
| [15] | 安恒斌, 莫则尧. JFNK方法迭代过程与物理约束[J]. 计算物理, 2012, 29(5): 654-660. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
