微管流中双囊泡惯性迁移的有限元分析

doi:10.19596/j.cnki.1001-246x.8755

摘要/Abstract

摘要：

采用基于流固耦合的有限元方法, 对二维模型中的双囊泡组合在微管流中惯性迁移现象进行系统研究。研究结果表明: 初始位置对称的两个圆形囊泡惯性迁移的平衡位置始终关于管道中央对称, 且随着雷诺数(Re)的增加, 其平衡位置会越来越靠近管道中央。其次, 对由圆形囊泡和椭圆形囊泡组成的双囊泡体系, 当圆形囊泡和椭圆形囊泡初始位置分别位于管道两侧时, 圆形囊泡惯性迁移的平衡位置随着雷诺数的增加几乎不变, 但椭圆形囊泡向管道中心偏移并跨过中心向管道另一侧偏移, 最后随着雷诺数的增加而缓慢向壁面移动, 并在Re≥500时, 椭圆形囊泡的径向位移达到最大值。当圆形囊泡和椭圆形囊泡位于管道同侧时, 随着雷诺数的增加, 无论椭圆形囊泡是前置或后置, 其最终平衡位置更接近管道壁面。根据囊泡的受力阐释了其背后的物理机制, 相关结果可促进惯性微流控技术在囊泡的精准分离和操控等方面的应用。

关键词: 双囊泡, 惯性迁移, 有限元

Abstract:

The finite element method based on fluid-structure interaction is used to systematically study the inertial migration of double vesicles in microtubule flow with a two-dimensional model. The results show that the equilibrium position of inertial migration of two circular vesicles with initial symmetry is always symmetric about the center of the channel, and with the increase of Reynolds number, the equilibrium position will be closer and closer to the center of the channel. Secondly, for the double vesicle system composed of circular vesicles and elliptic vesicles, when the initial positions of circular vesicles and elliptic vesicles are located on both sides of the channel, the equilibrium position of circular vesicle inertial migration is almost constant with the increase of Reynolds number, but the elliptic vesicles shift to the center of the channel and across the center to the other side of the channel, and finally move slowly to the wall with the increase of Reynolds number, and at Re≥500, the radial displacement of elliptic vesicle reaches the maximum value. When the circular and elliptical vesicles are located on the same side of the channel, the final equilibrium position is closer to the wall of the channel with the increase of Reynolds number, regardless of whether the elliptic vesicles are anterior or posterior. The present study elucidates the physical mechanism behind the vesicles based on their forces, and the related results can facilitate the application of inertial microfluidics in the precise separation and manipulation of vesicles.

Key words: double vesicles, inertial migration, finite element

中图分类号:

O469

刘烨琳, 郝鹏, 丁明明. 微管流中双囊泡惯性迁移的有限元分析[J]. 计算物理, 2024, 41(4): 463-471.

Yelin LIU, Peng HAO, Mingming DING. Finite Element Analysis of Inertial Migration of Double Vesicles in Microtubular Flow[J]. Chinese Journal of Computational Physics, 2024, 41(4): 463-471.

图/表 8

图1 不同初始位置时，双囊泡惯性迁移的模拟动态图

Fig.1 Dynamic simulation of double vesicles inertial migration at different initial positions

图2 不同阻塞比下，雷诺数对惯性迁移平衡位置的影响

Fig.2 Effect of Reynolds number on the equilibrium position of inertial migration with different blocking ratios

图3 不同阻塞比和不同雷诺数下囊泡升力随时间的变化

Fig.3 Plot of vesicle lift with time at different blocking ratios and different Reynolds numbers

图4 囊泡膜的模量和黏度对平衡位置的影响

Fig.4 Effect of vesicle membrane modulus and viscosity on equilibrium position

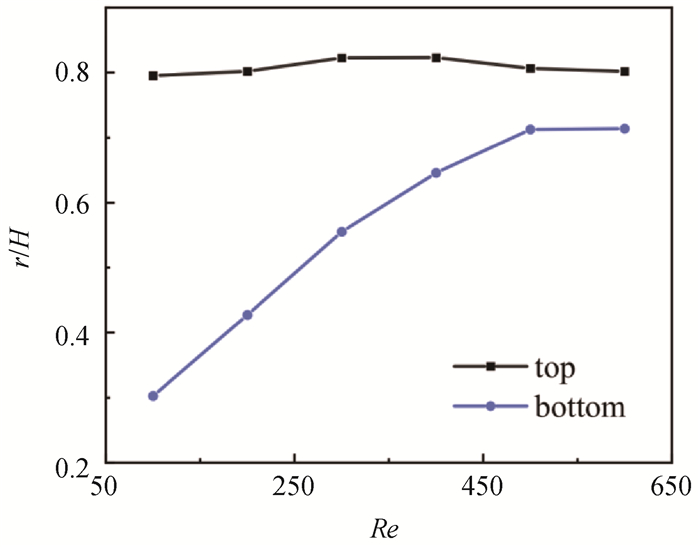
图5 上侧圆形囊泡、下侧椭圆形囊泡时，其平衡位置与体系雷诺数的关系

Fig.5 Relationship between equilibrium position of the upper circular vesicles and the lower elliptic vesicles and Reynolds number of the system

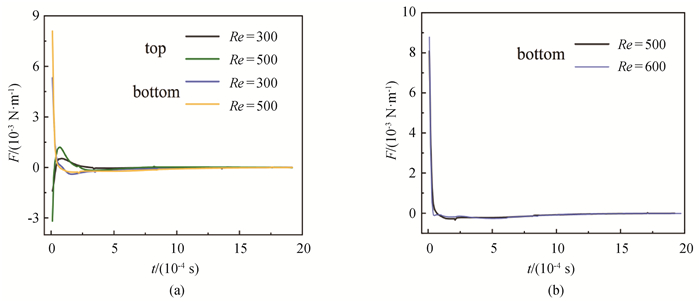
图6 (a) 圆形囊泡和椭圆形囊泡升力随时间的变化；(b)椭圆形囊泡升力随时间的变化

Fig.6 (a) Lift force of circular vesicles and elliptic vesicles with time; (b) lift force of elliptic vesicles with time

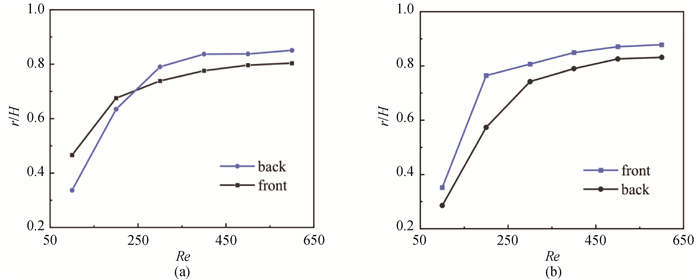
图7 双囊泡初始位置顺序不同时平衡位置的变化(蓝线为椭圆形囊泡，黑线为圆形囊泡。)

Fig.7 Variation of equilibrium position of double vesicles with different initial position order (Blue line is the elliptical vesicle, and the black line is circular vesicle.)

图8 双囊泡初始位置顺序不同时升力随时间的变化(a)和(b)圆形囊泡在前，椭圆形囊泡在后；(c)和(d)为椭圆形囊泡在前，圆形囊泡在后

Fig.8 Variation of lift force of double vesicles at different initial positions order with time (a) and (b) circular vesicle in front and elliptic vesicles inback; (c) and (d) elliptic vesicle in front and circular vesicle inback

参考文献 37

1	VAN HELL A J , COSTA C I C A , FLESCH F M , et al. Self-assembly of recombinant amphiphilic oligopeptides into vesicles[J]. Biomacromolecules, 2007, 8 (9): 2753- 2761. DOI
2	郝鹏, 张丽丽, 丁明明. 高分子囊泡在微管流中惯性迁移现象的有限元分析[J]. 物理学报, 2022, 71 (18): 363- 370.
3	YAMAMOTO S , MARUYAMA Y , HYODO S A . Dissipative particle dynamics study of spontaneous vesicle formation of amphiphilic molecules[J]. The Journal of Chemical Physics, 2002, 116 (13): 5842- 5849. DOI
4	杨艳霞, 李静. 膜生物反应器内生化反应过程的格子Boltzmann模拟[J]. 计算物理, 2018, 35 (5): 571- 576. DOI
5	ZHENG Wenfu , JIANG Xingyu . Precise manipulation of cell behaviors on surfaces for construction of tissue/organs[J]. Colloids and Surfaces B Biointerfaces, 2014, 124, 97- 110. DOI
6	CHOI Y S , SEO K W , LEE S J . Lateral and cross-lateral focusing of spherical particles in a square microchannel[J]. Lab on a Chip, 2011, 11 (3): 460- 465. DOI
7	LEE S J , BYEON H J , SEO K W . Inertial migration of spherical elastic phytoplankton in pipe flow[J]. Experiments in Fluids, 2014, 55 (6): 1742. DOI
8	SEGRÉ G , SILBERBERG A . Radial particle displacements in poiseuille flow of suspensions[J]. Nature, 1961, 189 (4760): 209- 210. DOI
9	CARLO D D , IRIMIA D , TOMPKINS R G , et al. Continuous inertial focusing, ordering, and separation of particles in microchannels[J]. PNAS, 2007, 104 (48): 18892- 18897. DOI
10	HUR S C , HENDERSON-MACLENNAN N K , MCCABE E R B , et al. Deformability-based cell classification and enrichment using inertial microfluidics[J]. Lab on a Chip, 2011, 11, 912- 920. DOI
11	KILIMNIL A , MAO Wenbin , ALEXEEV A . Inertial migration of deformable capsules in channel flow[J]. Physics of Fluids, 2011, 23 (12): 123302. DOI
12	RUBINOW S I , KELLER J B . The transverse force on a spinning sphere moving in a viscous fluid[J]. Journal of Fluid Mechanics, 1961, 11 (3): 447- 459. DOI
13	SAFFMAN P G . The lift on a small sphere in a slow shear flow[J]. Journal of Fluid Mechanics, 1965, 22 (2): 385- 400. DOI
14	YAN Yiguang , MORRIS J F , KOPLIK J . Hydrodynamic interaction of two particles in confined linear shear flow at finite Reynolds number[J]. Physics of Fluids, 2007, 19 (11): 13305.
15	SCHAAF C , RÜHLE F , STARK H . A flowing pair of particles in inertial microfluidics[J]. Soft Matter, 2019, 15 (9): 1988- 1998. DOI
16	SCHAAF C , STARK H . Particle pairs and trains in inertial microfluidics[J]. The European Physical Journal E, 2020, 43, 50- 63. DOI
17	LAC E , MOREL A , BARTHÈS-BIESEL D . Hydrodynamic interaction between two identical capsules in simple shear flow[J]. Journal of Fluid Mechanics, 2007, 573, 149- 169. DOI
18	KANTSLER V , SEGRE E , STEINBERG V . Dynamics of interacting vesicles and rheology of vesicle suspension in shear flow[J]. EPL, 2008, 82 (5): 58005. DOI
19	AOUANE O , FARUTIN A , THIÈBAUD M , et al. Hydrodynamic pairing of soft particles in a confined flow[J]. Physical Review Fluids, 2017, 2 (6): 063102. DOI
20	PATEL K , STARK H . A pair of particles in inertial microfluidics: effect of shape, softness, and position[J]. Soft Matter, 2021, 17 (18): 4804- 4817. DOI
21	LAN Hongzhi , KHISMATULLIN D B . Numerical simulation of the pairwise interaction of deformable cells during migration in a microchannel[J]. Physical Review E, 2014, 90 (1): 012705.
22	LI Ao , XU Gaoming , MA Jingtao , et al. Study on the binding focusing state of particles in inertial migration[J]. Applied Mathematical Modelling, 2021, 97, 1- 18. DOI
23	王坚毅, 潘振海, 吴慧英. 微通道内椭球颗粒惯性聚焦行为数值研究[J]. 计算物理, 2020, 37 (6): 677- 686. DOI
24	HAN Yunlong , LIN Hao , DING Mingming , et al. Flow-induced translocation of vesicles through a narrow pore[J]. Soft Matter, 2019, 15, 3307- 3314. DOI
25	雷体蔓, 孟旭辉, 郭照立. 微通道内反应流体粘性指进的数值研究[J]. 计算物理, 2016, 33 (1): 30- 38. DOI
26	ZHANG Ruilin , DING Mingming , DUAN Xiaozheng , et al. Electrohydrodynamic behavior of polyelectrolyte vesicle accompanied with ions in solution through a narrow pore induced by electric field[J]. Physics of Fluids, 2021, 33 (12): 121901. DOI
27	ZHANG Yuling , HAN Yunlong , ZHANG Lili , et al. Dynamic mode of viscoelastic capsules in steady and oscillating shear flow[J]. Physics of Fluids, 2020, 32 (10): 103310. DOI
28	TAKEISHI N , YAMASHITA H , OMORI T , et al. Inertial migration of red blood cells under a Newtonian fluid in a circular channel[J]. Journal of Fluid Mechanics, 2022, 952, A35. DOI
29	ZHANG Ruilin , HAN Yunlong , ZHANG Lili , et al. Migration and deformation of polyelectrolyte vesicle through a pore in electric field[J]. Colloids and Surfaces. a, Physicochemical and Engineering Aspects, 2021, 609, 125560. DOI
30	ZHOU Jian , VOROBYEVA A , LUAN Qiyue , et al. Single cell analysis of inertial migration by circulating tumor cells and clusters[J]. Micromachines, 2023, 14 (4): 787. DOI
31	HAN Yunlong , LI Rui , DING Mingming , et al. Dynamics of a rodlike deformable particle passing through a constriction[J]. Physics of Fluids, 2021, 33 (1): 012010. DOI
32	LI Yingxiang , XING Baohua , DING Mingming , et al. Flow-driven competition between two capsules passing through a narrow pore[J]. Soft Matter, 2021, 17 (40): 9154- 9161. DOI
33	HAN Yunlong , DING Mingming , LI Rui , et al. Kinematics of non-axially positioned vesicles through a Pore[J]. Chinese Journal of Polymer Science, 2020, 38 (7): 776- 783. DOI
34	ESPINO D M , SHEPHERD D E T , HUKINS D W L . Transient large strain contact modelling: A comparison of contact techniques for simultaneous fluid-structure interaction[J]. European Journal of Mechanics-B/Fluids, 2015, 51, 54- 60. DOI
35	HOTZ J , MEIER W . Vesicle-templated polymer hollow spheres[J]. Langmuir, 1998, 14 (5): 1031- 1036. DOI
36	FENG J , HU H H , JOSEPH D D . Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid. Part 2. Couette and Poiseuille flows[J]. Journal of Fluid Mechanics, 1994, 277, 271- 301. DOI
37	BRENNER H . The slow motion of a sphere through a viscous fluid towards a plane surface[J]. Chemical Engineering Science, 1961, 16 (3/4): 242- 251.

[1]	王雅莉, 郑波, 尚月强. 定常不可压Navier-Stokes方程的两水平grad-div稳定化有限元方法[J]. 计算物理, 2024, 41(4): 418-425.
[2]	唐熊, 郑佩. 基于对数应变的孔隙黏弹性有限变形理论[J]. 计算物理, 2024, 41(3): 287-297.
[3]	范鹤潇, 陈星玎. 一类求解含静态裂缝线弹性问题的预条件扩展有限元方法[J]. 计算物理, 2024, 41(2): 151-160.
[4]	高普阳. 三维非等温聚合物熔体充填问题的相场方法[J]. 计算物理, 2023, 40(6): 689-698.
[5]	王国梁, 郑波, 尚月强. 带阻尼项定常Navier-Stokes方程的并行两水平有限元算法[J]. 计算物理, 2023, 40(5): 535-547.
[6]	麦兴鸿, 陈巧悦, 丁明明. 重力作用下软球壳堆积结构的有限元分析[J]. 计算物理, 2023, 40(3): 359-368.
[7]	王湛煌, 郑波, 尚月强. 非定常Navier-Stokes方程的并行两水平稳定有限元算法[J]. 计算物理, 2023, 40(1): 14-28.
[8]	朱家莉, 尚月强. 不可压缩流的并行两水平稳定有限元算法[J]. 计算物理, 2022, 39(3): 309-317.
[9]	李宏明, 李茂生. 晶体塑性有限元方法研究辐照对多晶铜力学性能的影响[J]. 计算物理, 2022, 39(1): 6-16.
[10]	高普阳. 聚合物充填过程中裹气现象的数值模拟[J]. 计算物理, 2021, 38(6): 693-706.
[11]	杜丹, 李帅, 阳璞琼, 冯军, 向东, 龚学余. 螺旋天线轴向长度对螺旋波传播、吸收的影响[J]. 计算物理, 2021, 38(6): 713-721.
[12]	丁琪, 尚月强. 非定常Navier-Stokes方程基于两重网格离散的有限元并行算法[J]. 计算物理, 2020, 37(1): 10-18.
[13]	张庆福, 姚军, 黄朝琴, 李阳, 王月英. 裂缝性介质多尺度深度学习模型[J]. 计算物理, 2019, 36(6): 665-672.
[14]	温小静, 屈瑜, 陈城钊. 双层开口环的圆二色性数值研究[J]. 计算物理, 2019, 36(3): 357-362.
[15]	陈恭, 王一正, 王烨, 张纯禹. 缩减基有限元方法快速求解参数化偏微分方程[J]. 计算物理, 2018, 35(5): 515-524.