计算物理 ›› 2025, Vol. 42 ›› Issue (2): 211-223.DOI: 10.19596/j.cnki.1001-246x.8878
收稿日期:2023-12-21
出版日期:2025-03-25
发布日期:2025-04-08
通讯作者:
尚月强
作者简介:徐彤, 硕士研究生, 研究方向为偏微分方程数值解, E-mail: xtong1214@163.com
基金资助:
Tong XU( ), Yueqiang SHANG*(
), Yueqiang SHANG*( )
)
Received:2023-12-21
Online:2025-03-25
Published:2025-04-08
Contact:
Yueqiang SHANG
摘要:
针对带非线性阻尼项定常不可压缩Stokes问题, 提出两种基于有限元离散的数值迭代算法, 其基本思想是: 首先使用有限元法求解Stokes问题, 得到迭代初始解; 其次, 运用Stokes迭代算法或Oseen迭代算法求解带非线性阻尼项定常不可压缩Stokes问题, 得到有限元近似解。证明算法的收敛性和稳定性, 并给出了相应的误差估计; 通过4个数值实验, 验证了理论分析的正确性和算法的有效性。研究结果表明: 当方程满足稳定性条件时, 两种数值迭代算法都是可行的。
徐彤, 尚月强. 带非线性阻尼项定常Stokes方程的有限元迭代算法[J]. 计算物理, 2025, 42(2): 211-223.
Tong XU, Yueqiang SHANG. Finite Element Iterative Algorithms for Steady Stokes Equations with Nonlinear Damping Term[J]. Chinese Journal of Computational Physics, 2025, 42(2): 211-223.
| 算法 | 1/h | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | UH1 | PL2 |
| Stokes迭代 | 20 | 0.335 | 3 | 2.095 04 × 10-4 | 7.905 69 × 10-4 | ||
| 30 | 0.745 | 3 | 9.342 65 × 10-5 | 3.513 64 × 10-4 | 1.991 71 | 2 | |
| 40 | 1.43 | 3 | 5.261 72 × 10-5 | 1.976 42 × 10-4 | 1.995 72 | 2 | |
| 50 | 2.418 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.997 38 | 2 | |
| 60 | 3.659 | 3 | 2.340 67 × 10-5 | 8.784 10 × 10-5 | 1.998 23 | 2 | |
| 70 | 5.409 | 3 | 1.720 01 × 10-5 | 6.453 63 × 10-5 | 1.998 72 | 2 | |
| Oseen迭代 | 20 | 0.236 | 2 | 2.095 04 × 10-4 | 7.905 69 × 10-4 | ||
| 30 | 0.538 | 2 | 9.342 65 × 10-5 | 3.513 64 × 10-4 | 1.991 71 | 2 | |
| 40 | 1.033 | 2 | 5.261 72 × 10-5 | 1.976 42 × 10-4 | 1.995 72 | 2 | |
| 50 | 1.748 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.997 38 | 2 | |
| 60 | 2.64 | 2 | 2.340 67 × 10-5 | 8.784 1 × 10-5 | 1.998 23 | 2 | |
| 70 | 4.012 | 2 | 1.720 01 × 10-5 | 6.453 63 × 10-5 | 1.998 72 | 2 |
表1 二维情形下Stokes迭代算法与Oseen迭代算法误差比较(ν=0.01, α=0.1)
Table 1 Errors of Stokes iterative algorithm and Oseen iterative algorithm in 2D (ν=0.01, α=0.1)
| 算法 | 1/h | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | UH1 | PL2 |
| Stokes迭代 | 20 | 0.335 | 3 | 2.095 04 × 10-4 | 7.905 69 × 10-4 | ||
| 30 | 0.745 | 3 | 9.342 65 × 10-5 | 3.513 64 × 10-4 | 1.991 71 | 2 | |
| 40 | 1.43 | 3 | 5.261 72 × 10-5 | 1.976 42 × 10-4 | 1.995 72 | 2 | |
| 50 | 2.418 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.997 38 | 2 | |
| 60 | 3.659 | 3 | 2.340 67 × 10-5 | 8.784 10 × 10-5 | 1.998 23 | 2 | |
| 70 | 5.409 | 3 | 1.720 01 × 10-5 | 6.453 63 × 10-5 | 1.998 72 | 2 | |
| Oseen迭代 | 20 | 0.236 | 2 | 2.095 04 × 10-4 | 7.905 69 × 10-4 | ||
| 30 | 0.538 | 2 | 9.342 65 × 10-5 | 3.513 64 × 10-4 | 1.991 71 | 2 | |
| 40 | 1.033 | 2 | 5.261 72 × 10-5 | 1.976 42 × 10-4 | 1.995 72 | 2 | |
| 50 | 1.748 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.997 38 | 2 | |
| 60 | 2.64 | 2 | 2.340 67 × 10-5 | 8.784 1 × 10-5 | 1.998 23 | 2 | |
| 70 | 4.012 | 2 | 1.720 01 × 10-5 | 6.453 63 × 10-5 | 1.998 72 | 2 |
| 算法 ν | Stokes迭代 | Oseen迭代 | |||||||
| CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | ||
| 10-2 | 2.422 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 2.015 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10-3 | 3.073 | 4 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 2.43 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10-4 | 5.584 | 8 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 4.227 | 6 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
表2 不同ν值下Stokes迭代算法与Oseen迭代算法的数值结果(h=1/50, α=0.1)
Table 2 Numerical results of Stokes iterative algorithm and Oseen iterative algorithm with different ν (h=1/50, α=0.1)
| 算法 ν | Stokes迭代 | Oseen迭代 | |||||||
| CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | ||
| 10-2 | 2.422 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 2.015 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10-3 | 3.073 | 4 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 2.43 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10-4 | 5.584 | 8 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 4.227 | 6 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 算法 α | Stokes迭代 | Oseen迭代 | |||||||
| CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | ||
| 10-2 | 1.898 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.824 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10-1 | 2.481 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.834 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 1 | 3.139 | 4 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 2.464 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10 | 5.985 | 8 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 4.221 | 6 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 102 | 不收敛 | 13.762 | 21 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | ||||
表3 不同α值下Stokes迭代算法与Oseen迭代算法的数值结果(h=1/50, ν=0.01)
Table 3 Numerical results of Stokes iterative algorithm and Oseen iterative algorithm with different α (h=1/50, ν=0.01)
| 算法 α | Stokes迭代 | Oseen迭代 | |||||||
| CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | ||
| 10-2 | 1.898 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.824 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10-1 | 2.481 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 1.834 | 2 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 1 | 3.139 | 4 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 2.464 | 3 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 10 | 5.985 | 8 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | 4.221 | 6 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | |
| 102 | 不收敛 | 13.762 | 21 | 3.369 47 × 10-5 | 1.264 91 × 10-4 | ||||
| 算法 | 1/h | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | UH1 | PL2 |
| Stokes迭代 | 4 | 2.121 | 9 | 3.998 29 | 1.619 09 × 10-2 | ||
| 6 | 6.699 | 4 | 1.363 89 | 7.195 61 × 10-3 | 2.652 57 | 2.000 12 | |
| 8 | 24.998 | 3 | 6.071 14 × 10-1 | 4.043 94 × 10-3 | 2.813 46 | 2.003 08 | |
| 10 | 96.683 | 3 | 3.201 99 × 10-1 | 2.586 44 × 10-3 | 2.867 10 | 2.002 92 | |
| 12 | 292.779 | 3 | 1.888 57 × 10-1 | 1.795 36 × 10-3 | 2.895 73 | 2.002 39 | |
| Oseen迭代 | 4 | 1.177 | 5 | 3.998 29 | 1.619 09 × 10-2 | ||
| 6 | 5.24 | 3 | 1.363 89 | 7.195 61 × 10-3 | 2.652 57 | 2.000 12 | |
| 8 | 24.364 | 3 | 6.071 14 × 10-1 | 4.043 94 × 10-3 | 2.81 346 | 2.003 08 | |
| 10 | 96.116 | 3 | 3.201 99 × 10-1 | 2.586 44 × 10-3 | 2.867 10 | 2.002 92 | |
| 12 | 289.645 | 3 | 1.888 57 × 10-1 | 1.795 36 × 10-3 | 2.895 73 | 2.002 39 |
表4 三维情形下Stokes迭代算法与Oseen迭代算法误差(ν=0.001, α=0.1)
Table 4 Errors between Stokes iterative algorithm and Oseen iterative algorithm in 3D (ν=0.001, α=0.1)
| 算法 | 1/h | CPU/s | it | ‖▽(u-uhn)‖ | ‖p-phn‖ | UH1 | PL2 |
| Stokes迭代 | 4 | 2.121 | 9 | 3.998 29 | 1.619 09 × 10-2 | ||
| 6 | 6.699 | 4 | 1.363 89 | 7.195 61 × 10-3 | 2.652 57 | 2.000 12 | |
| 8 | 24.998 | 3 | 6.071 14 × 10-1 | 4.043 94 × 10-3 | 2.813 46 | 2.003 08 | |
| 10 | 96.683 | 3 | 3.201 99 × 10-1 | 2.586 44 × 10-3 | 2.867 10 | 2.002 92 | |
| 12 | 292.779 | 3 | 1.888 57 × 10-1 | 1.795 36 × 10-3 | 2.895 73 | 2.002 39 | |
| Oseen迭代 | 4 | 1.177 | 5 | 3.998 29 | 1.619 09 × 10-2 | ||
| 6 | 5.24 | 3 | 1.363 89 | 7.195 61 × 10-3 | 2.652 57 | 2.000 12 | |
| 8 | 24.364 | 3 | 6.071 14 × 10-1 | 4.043 94 × 10-3 | 2.81 346 | 2.003 08 | |
| 10 | 96.116 | 3 | 3.201 99 × 10-1 | 2.586 44 × 10-3 | 2.867 10 | 2.002 92 | |
| 12 | 289.645 | 3 | 1.888 57 × 10-1 | 1.795 36 × 10-3 | 2.895 73 | 2.002 39 |
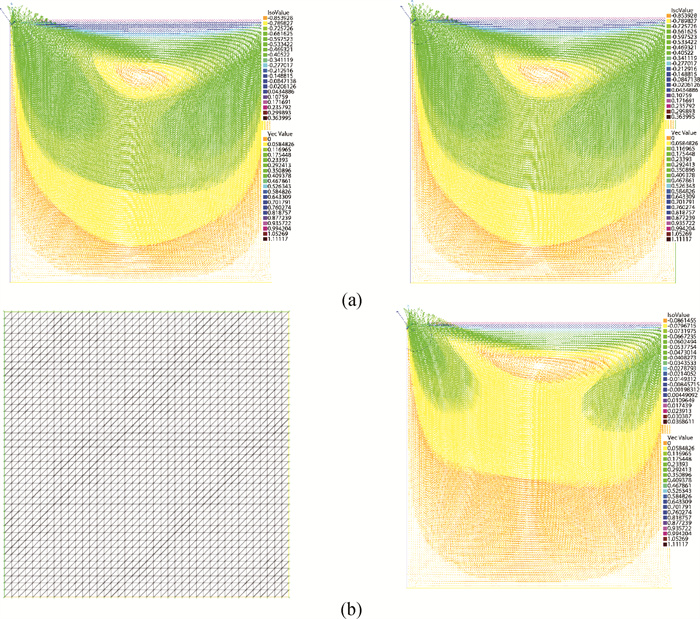
图1 在不同黏性系数ν下的Stokes迭代算法(左列)与Oseen迭代算法(右列)的有限元解(a) ν=10-3;(b) ν=10-4
Fig.1 Finite element solutions of Stokes iterative algorithm (left) and Oseen iterative algorithm (right) with different ν (a) ν=10-3; (b) ν=10-4
| 算法 ν | Stokes迭代 | Oseen迭代 | |||
| CPU/s | it | CPU/s | it | ||
| 10-3 | 6.998 | 20 | 3.345 | 9 | |
| 10-4 | 不收敛 | 不收敛 | 6.809 | 19 | |
表5 不同黏性系数ν下Stokes迭代与Oseen迭代的数值结果
Table 5 Numerical results of Stokes iteration and Oseen iteration with different ν
| 算法 ν | Stokes迭代 | Oseen迭代 | |||
| CPU/s | it | CPU/s | it | ||
| 10-3 | 6.998 | 20 | 3.345 | 9 | |
| 10-4 | 不收敛 | 不收敛 | 6.809 | 19 | |
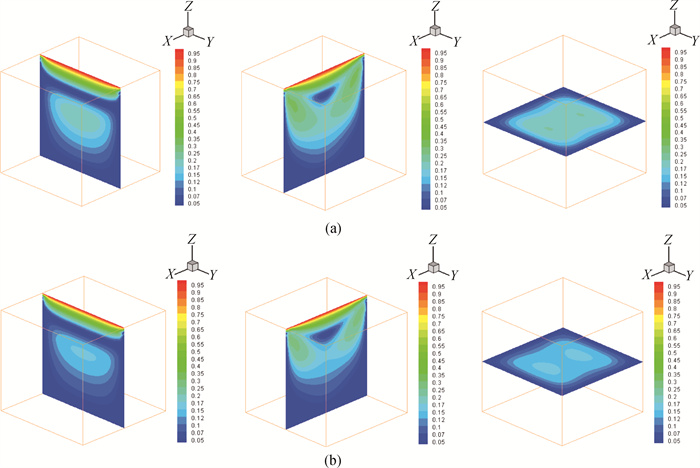
图2 在不同ν值下Oseen迭代算法三维方腔驱动流的速度近似解(左列: X平面, 中列: Y平面, 右列: Z平面)(a) ν=10-2;(b) ν=10-3
Fig.2 Computed velocity for 3D square cavity driven flow by Oseen iterative algorithm with different values of ν (left: X plane, middle: Y plane, right: Z plane) (a) ν=10-2; (b) ν=10-3
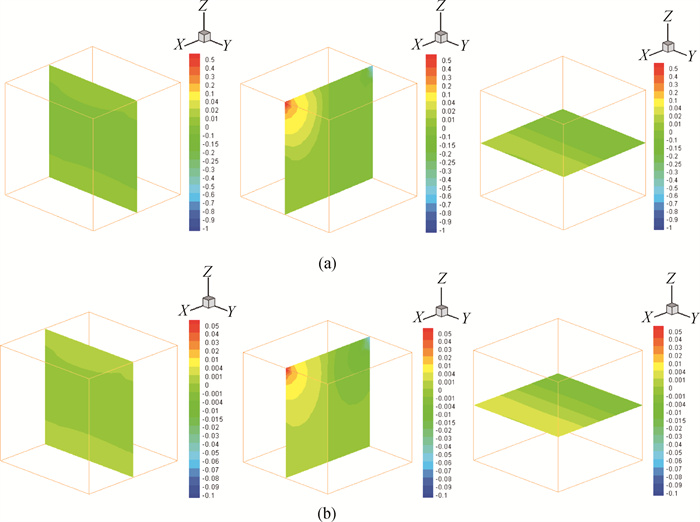
图3 在不同ν值下Oseen迭代算法三维方腔驱动流的压力近似解(左列: X平面, 中列: Y平面, 右列: Z平面)(a) ν=10-2;(b) ν=10-3
Fig.3 Computed pressure for 3D square cavity driven flow by Oseen iterative algorithm with different values of ν (left: X plane, middle: Y plane, right: Z plane) (a) ν=10-2; (b) ν=10-3
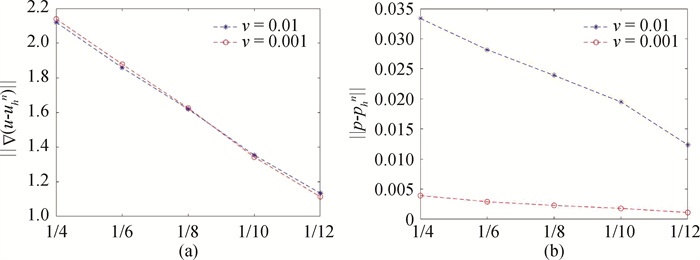
图4 Oseen迭代算法下(a)速度H1误差和(b)压力L2误差的变化趋势(α=0.1)
Fig.4 Evolution of (a) H1-error for velocity and (b) L2-error for the pressure with Oseen iterative algorithm (α=0.1)
| 1 |
DOI |
| 2 |
DOI |
| 3 |
DOI |
| 4 |
DOI |
| 5 |
DOI |
| 6 |
DOI |
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
王雅莉, 郑波, 尚月强. 定常不可压Navier-Stokes方程的两水平grad-div稳定化有限元方法[J]. 计算物理, 2024, 41(4): 418- 425.
DOI |
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
DOI |
| 15 |
DOI |
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
TEMAM R. Navier-stokes equations: theory and numerical analysis[M]. Amsterdam, New York: North-Holland Pub. Co., 1984.
|
| 22 |
DOI |
| 23 |
DOI |
| 24 |
DOI |
| 25 |
|
| 26 |
DOI |
| 27 |
|
| [1] | 赵腾飞, 张华. 均匀风场作用下黏性可压缩射流稳定性分析[J]. 计算物理, 2025, 42(1): 1-9. |
| [2] | 尹林茂, 张玉龙, 杨洋, 肖福建, 蒋秉颜. 一种基于Picard迭代求解不可压缩Navier-Stokes方程的速度修正投影法[J]. 计算物理, 2025, 42(1): 10-17. |
| [3] | 肖梦娟, 谢寒松, 宾远为, 张又升. 面向工程应用的流体界面失稳湍流混合问题建模进展[J]. 计算物理, 2024, 41(6): 732-745. |
| [4] | 王雅莉, 郑波, 尚月强. 定常不可压Navier-Stokes方程的两水平grad-div稳定化有限元方法[J]. 计算物理, 2024, 41(4): 418-425. |
| [5] | 欧阳思杰, 胡双辉, 欧阳学峰, 朱万坡, 兰源丹, 黄旋格. ITER具有内部输运垒方案中的离散阿尔芬本征模[J]. 计算物理, 2023, 40(6): 677-688. |
| [6] | 王国梁, 郑波, 尚月强. 带阻尼项定常Navier-Stokes方程的并行两水平有限元算法[J]. 计算物理, 2023, 40(5): 535-547. |
| [7] | 朱万坡, 胡双辉, 欧阳学锋, 欧阳思杰, 兰源丹. EAST高约束运行条件下离散阿尔芬本征模的数值模拟[J]. 计算物理, 2023, 40(4): 461-472. |
| [8] | 徐敬坤, 汪卫华. EAST通行高能粒子激发的非共振鱼骨模不稳定性模拟[J]. 计算物理, 2023, 40(3): 291-300. |
| [9] | 蔡洪波, 许育培, 姚沛霖, 张恩浩, 黄翰霄, 朱少平, 贺贤土. 混合流体-PIC物理建模及其在激光聚变中的应用[J]. 计算物理, 2023, 40(2): 159-168. |
| [10] | 王湛煌, 郑波, 尚月强. 非定常Navier-Stokes方程的并行两水平稳定有限元算法[J]. 计算物理, 2023, 40(1): 14-28. |
| [11] | 张华, 杨明慧. 可压缩黏性圆射流稳定性分析[J]. 计算物理, 2022, 39(5): 529-536. |
| [12] | 唐利红, 贺宗梅, 姚延立. 具有隐藏超级多稳定性的磁感应HR神经元及其电路实现[J]. 计算物理, 2022, 39(5): 589-597. |
| [13] | 朱家莉, 尚月强. 不可压缩流的并行两水平稳定有限元算法[J]. 计算物理, 2022, 39(3): 309-317. |
| [14] | 薛创, 李馨东, 孙文俊, 叶文华, 彭先觉. 多介质五方程简化模型及界面捕捉的人工压缩算法[J]. 计算物理, 2021, 38(3): 257-268. |
| [15] | 曹启伟, 肖德龙, 杨显俊, 王建国. 磁瑞利-泰勒不稳定性非线性演化数值模拟[J]. 计算物理, 2021, 38(1): 5-15. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||
版权所有 © 《计算物理》编辑部
地址:北京市海淀区丰豪东路2号 邮编:100094 E-mail:jswl@iapcm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发
