金红石TiO2辐照损伤模拟研究

doi:10.19596/j.cnki.1001-246x.8700

摘要/Abstract

摘要：

利用分子动力学方法对金红石TiO₂中O及Ti沿着不同方向的离位阈能进行模拟计算，结果表明：各方向O的离位阈能普遍低于Ti的离位阈能，O的离位阈能基本在27.50~77.50 eV之间，而Ti的离位阈能在90.00~120.00 eV之间。同时对能量为1.0、5.0和10.0 keV的O PKA及Ti PKA造成的级联辐照损伤进行探究，结果表明：能量小于10.0 keV的O PKA及Ti PKA产生的主要是点缺陷，且点缺陷的数量在0.10~0.20 ps内达到峰值，在经过数ps的演化后，超过90.0%以上的缺陷复合，只有不足10.0%的缺陷保留下来，即金红石TiO₂中的缺陷在缺陷产生初期有较高的自我恢复能力。

关键词: 金红石TiO₂, 离位阈能, 级联损伤, 分子动力学

Abstract:

In this study, threshold displacement energy of O and Ti in rutile TiO₂ along different directions is simulated by using the method of molecular dynamics. Simulation results show that threshold displacement energy of O atom in all directions is generally lower than that of Ti atom. The threshold displacement energy of O is basically between 27.50 and 77.50 eV, while that of Ti is between 90.00 and 120.00 eV. Meanwhile, this study also explores the cascade radiation damage caused by O PKA and Ti PKA with energy of 1.0, 5.0 and 10.0 keV. Cascade radiation damage results show that O PKA and Ti PKA with energy less than 10.0 keV mainly produced point defects. The number of point defects reached the peak within 0.10~0.20 ps. After several ps evolution, more than 90.0% of the defects are annealing, and only less than 10.0% defects remained. In other words, the defects in rutile TiO₂ have higher self-recovery ability at the initial stage of defect generation.

Key words: rutile TiO₂, threshold displacement energy, cascade damage, molecular dynamics

中图分类号:

TQ174

高旭东, 孙淑义, 魏雯静, 李公平. 金红石TiO₂辐照损伤模拟研究[J]. 计算物理, 2024, 41(2): 214-221.

Xudong GAO, Shuyi SUN, Wenjing WEI, Gongping LI. A Simulation Study on Irradiation Damage of Rutile TiO₂[J]. Chinese Journal of Computational Physics, 2024, 41(2): 214-221.

图/表 8

表1 势函数参数表

Table 1 Potential parameters

	O-O	Ti-Ti	Ti-O
r₁/nm	0.02	0.04	0.06
r₂/nm	0.04	0.10	0.16
r_c/nm		0.65

图1 模拟结构示意图

Fig.1 Schematic diagram of simulation structure

图2 体系的势能及温度随弛豫时间的变化

Fig.2 The curve of potential energy and temperature of the system with relaxation time

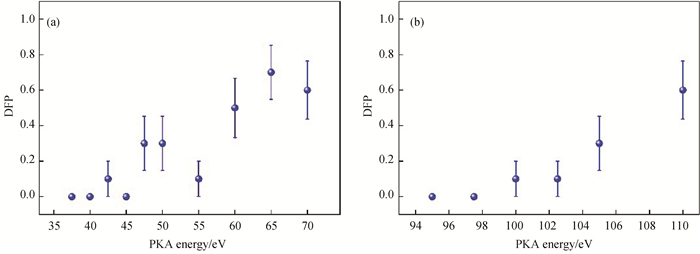
图3 DFP随PKA能量的变化关系(a)O PKA沿着[111]方向；(b)Ti PKA沿着[010]方向

Fig.3 The variation of DFP with PKA energy (a) O PKA along [111] direction; (b) Ti PKA along [010] direction

表2 金红石TiO2中O原子及Ti原子Ed的计算结果

Table 2 Statistical results of Ed in rutile TiO2

PKA direction	E_d/eV
PKA direction	O	Ti
[100]	27.50±2.50、30±5.0^[17]	92.50±2.50、115±5.0^[17]、约52^[15]
[010]	50.00±2.50	100.00±2.50
[001]	77.50±2.50、65±5.0^[17]	90.00±2.50、80±5.0^[17]、约47^[15]
[110]	67.50±2.50、55±5.0^[17]	90.00±2.50、100±5.0^[17]
[111]	42.50±2.50、35±5.0^[17]	120.00±2.50、160±5.0^[17]、约50^[15]
Avg.value	19^[18]、39±5^[16]	69^[18]、50^[16]

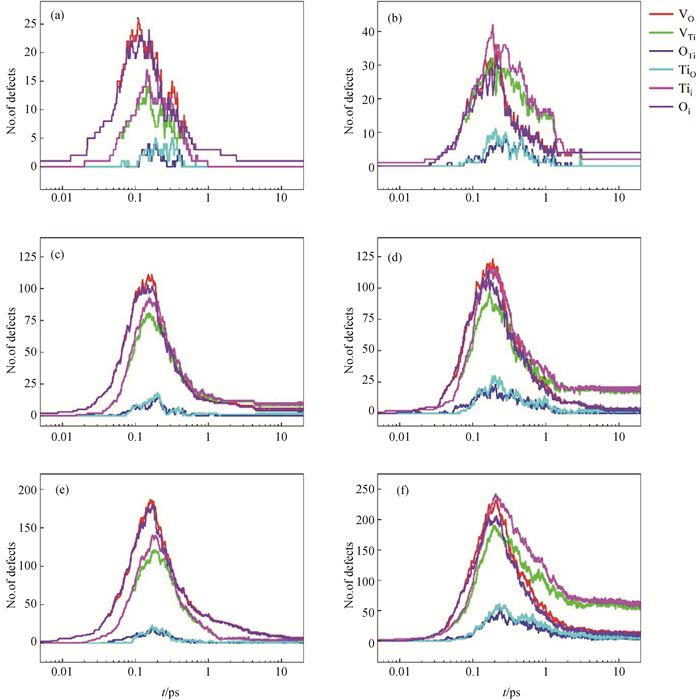
图4 缺陷数目随时间演化关系图(a) O PKA：1.0 keV；(b) Ti PKA：1.0 keV；(c) O PKA：5.0 keV；(d) Ti PKA：5.0 keV；(e) O PKA：10.0 keV；(f) Ti PKA：10.0 keV

Fig.4 Diagram of defect number evolution with time (a) O PKA: 1.0 keV; (b) Ti PKA: 1.0 keV; (c) O PKA: 5.0 keV; (d) Ti PKA: 5.0 keV; (e) O PKA: 10.0 keV; (f) Ti PKA: 10.0 keV

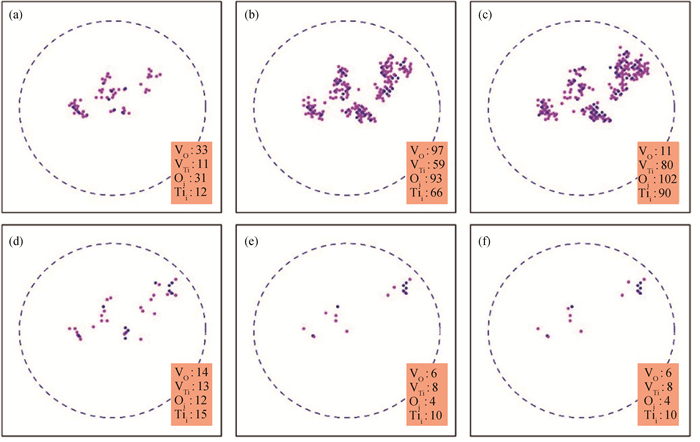
图5 5.0 keV的O PKA产生的缺陷演化趋势图(a) 0.05 ps；(b) 0.10 ps；(c) 0.15 ps；(d) 1.00 ps；(e) 10.00 ps；(f) 15.00 ps

Fig.5 Schematic diagrams of defect evolution by O PKA at 5.0 keV (a) 0.05 ps; (b) 0.10 ps; (c) 0.15 ps; (d) 1.00 ps; (e) 10.00 ps; (f) 15.00 ps

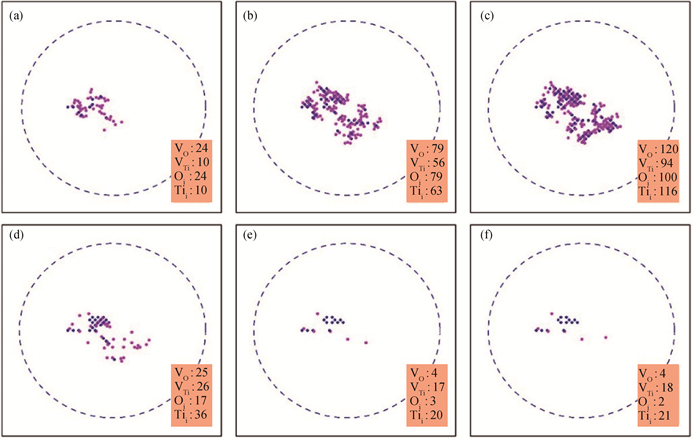
图6 5.0 keV的Ti PKA产生的缺陷演化趋势图(a) 0.05 ps；(b) 0.10 ps；(c) 0.15 ps；(d) 1.00 ps；(e) 10.00 ps；(f) 15.00 ps

Fig.6 Schematic diagrams of defect evolution by Ti PKA at 5.0 keV (a) 0.05 ps; (b) 0.10 ps; (c) 0.17 ps; (d) 1.00 ps; (e) 10.00 ps; (f) 15.00 ps

参考文献 35

1	MATSUMOTO Y , MURAKAMI M , SHONO T , et al. Room-temperature ferromagnetism in transparent transition metal-doped titanium dioxide[J]. Science, 2001, 291 (5505): 854- 856. DOI
2	WOLF S A , AWSCHALOM D D , BUHRMAN R A , et al. Spintronics: A spin-based electronics vision for the future[J]. Science, 2001, 294 (5546): 1488- 1495. DOI
3	Li P Y , WU Z M , YE Q , et al. First-principles calculation of Mn-doped LiMgN diluted magnetic semiconductor[J]. Chinese Journal of Computational Physics, 2018, 35 (1): 103- 111.
4	HIROHATA A , YAMADA K , NAKATANI Y , et al. Review on spintronics: Principles and device applications[J]. Journal of Magnetism and Magnetic Materials, 2020, 509, 166711. DOI
5	SONG C , ZHANG R Q , LIAO L Y , et al. Spin-orbit torques: Materials, mechanisms, performances, and potential applications[J]. Progress in Materials Science, 2021, 118, 100761. DOI
6	HUANG W Q , LIN R , CHEN W J , et al. High room-temperature magnetization in Co-doped TiO₂ nanoparticles promoted by vacuum annealing for different durations[J]. Journal of Semiconductors, 2021, 42 (7): 072501. DOI
7	ZHAO Q A , WU P . Ferromagnetism induced by defects in Cr-doped TiO₂ nanopowders[J]. Journal of Inorganic Materials, 2013, 28 (10): 1098- 1102. DOI
8	CHOUHAN L , SRIVASTAVA S K . Observation of room temperature d⁰ ferromagnetism, band-gap widening, zero dielectric loss and conductivity enhancement in Mg doped TiO₂ (rutile+anatase) compounds for spintronics applications[J]. Journal of Solid State Chemistry, 2022, 307, 122828. DOI
9	RINGWOOD A E , KESSON S E , WARE N G , et al. Immobilisation of high level nuclear reactor wastes in SYNROC[J]. Nature, 1979, 278 (5701): 219- 223. DOI
10	NAKAGAWA M , OKADA M , ITOH H , et al. Lattice deffects in rutile, TiO₂[J]. Radiation Effects and Defects in Solids, 1991, 119-121 (1): 153- 157. DOI
11	LUMPKIN G R , SMITH K L , BLACKFORD M G , et al. Experimental and atomistic modeling study of ion irradiation damage in thin crystals of the TiO₂ polymorphs[J]. Physical Review B, 2008, 77 (21): 214201. DOI
12	唐万平, 丁晶洁, 李公平, 等. 2种耐核辐射涂料的耐辐照性能研究[J]. 涂料工业, 2018, 48 (12): 47- 53.
13	GRAY R L , RUSHTON M J D , MURPHY S T . Molecular dynamics simulations of radiation damage in YBa₂Cu₃O₇[J]. Superconductor Science and Technology, 2022, 35 (3): 035010. DOI
14	MORRIS J , COWEN B J , TEYSSEYRE S , et al. Molecular dynamics investigation of threshold displacement energies in CaF₂[J]. Computational Materials Science, 2020, 172, 109293. DOI
15	BUCK E C . Effects of electron irradiation of rutile[J]. Radiation Effects and Defects in Solids, 1995, 133 (2): 141- 152. DOI
16	SMITH K L , COLELLA M , COOPER R , et al. Measured displacement energies of oxygen ions in titanates and zirconates[J]. Journal of Nuclear Materials, 2003, 321 (1): 19- 28. DOI
17	THOMAS B S , MARKS N A , CORRALES L R , et al. Threshold displacement energies in rutile TiO₂: A molecular dynamics simulation study[J]. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2005, 239 (3): 191- 201.
18	ROBINSON M , MARKS N A , WHITTLE K R , et al. Systematic calculation of threshold displacement energies: Case study in rutile[J]. Physical Review B, 2012, 85 (10): 104105. DOI
19	ROBINSON M , MARKS N A , LUMPKIN G R . Sensitivity of the threshold displacement energy to temperature and time[J]. Physical Review B, 2012, 86 (13): 134105. DOI
20	COWEN B J , EI-GENK M S . Directional dependence of the threshold displacement energies in metal oxides[J]. Modelling and Simulation in Materials Science and Engineering, 2017, 25 (8): 085009. DOI
21	JACKSON M L , FOSSATI P C M , GRIMES R M . Simulations of threshold displacement in beryllium[J]. Journal of Applied Physics, 2016, 120 (4): 045903. DOI
22	TANG P F , ZHENG Q R , LI J W , et al. Cluster dynamics modeling with spatial correlations in cascades[J]. Chinese Journal of Computational Physics, 2019, 36 (5): 586- 594.
23	ZHANG X Y , CHEN X F , WANG H , et al. Molecular dynamics analysis of chemical disorders induced by irradiated point defects in 6H-SiC[J]. Journal of Inorganic Materials, 2020, 35 (8): 889- 894. DOI
24	THOMPSON A P , AKTULGA H M , BERGER R , et al. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales[J]. Computer Physics Communications, 2022, 271, 108171. DOI
25	MATSUI M , AKAOGI M . Molecular dynamics simulation of the structural and physical properties of the four polymorphs of TiO₂[J]. Molecular Simulation, 1991, 6 (4-6): 239- 244. DOI
26	BOLZAN A A , FONG C , KENNEDY B J , et al. Structural studies of rutile-type metal dioxides[J]. Acta Crystallographica Section B-Structural Science, 1997, 53 (3): 373- 380. DOI
27	STUKOWSKI A . Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool[J]. Modelling and Simulation in Materials Science and Engineering, 2010, 18 (1): 015012. DOI
28	GONZALEZ E , ABREU Y , CRUZ C M , et al. Molecular-dynamics simulation of threshold displacement energies in BaTiO₃[J]. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2015, 358, 142- 145.
29	COWEN B J , EL-GENK M S . Point defects production and energy thresholds for displacements in crystalline and amorphous SiC[J]. Computational Materials Science, 2018, 151, 73- 83. DOI
30	THOMAS B S , MARKS N A , BEGG B D . Defects and threshold displacement energies in SrTiO₃ perovskite using atomistic computer simulations[J]. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2007, 254 (2): 211- 218.
31	ZIEGLER J F , ZIEGLER M D , BIERSACK J P . SRIM-the stopping and range of ions in matter (2010)[J]. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2010, 268 (11/12): 1818- 1823.
32	NORDLUND K , ZINKLE S J , SAND A E , et al. Improving atomic displacement and replacement calculations with physically realistic damage models[J]. Nature Communications, 2018, 9 (1): 1084. DOI
33	CAI J , LU D G , MA Y , et al. Structure evolution of defects in BCC iron by dislacement cascade: Molecular dynamics simulation[J]. Chinese Journal of Computational Physics, 2011, 28 (6): 915- 921.
34	GAO X D , LV L L , ZHANG Z H , et al. A simulation study on the electromagnetic structure and optical properties of Co doped TiO₂[J]. Computational Materials Science, 2022, 209, 111404. DOI
35	COWEN B J , EL-GENK M S . Characterization of radiation damage in TiO₂ using molecular dynamics simulations[J]. Modelling and Simulation in Materials Science and Engineering, 2018, 26 (8): 085005. DOI

[1]	温伯尧, 高根英, 路熙, 关松涛, 骆政园, 白博峰. 球状胶束中表面活性剂脱附的离子调控机制[J]. 计算物理, 2024, 41(2): 193-202.
[2]	李禹, 刘慧卿, 冯亚斌, 东晓虎, 王庆, 张波. 典型表活剂与稠油在蒙脱石表面吸附行为的分子动力学模拟[J]. 计算物理, 2023, 40(5): 583-596.
[3]	韦昭召, 刘凯, 李会军. NiAl合金纳米线弯曲形变行为的分子动力学模拟[J]. 计算物理, 2023, 40(4): 425-435.
[4]	侯兆阳, 牛媛, 肖启鑫, 王真, 邓庆田. Al纳米线不同晶向力学行为和变形机制的模拟[J]. 计算物理, 2022, 39(3): 341-351.
[5]	王晓慧, 张平. 高压下FCC相金属氢结构稳定性和非谐效应的理论研究[J]. 计算物理, 2022, 39(2): 159-164.
[6]	阿湖宝, 杨志兵, 胡冉, 陈益峰. 纳米尺度下毛细流动的分子动力学模拟[J]. 计算物理, 2021, 38(5): 603-611.
[7]	王国华, 崔雅茹, 杨泽, 李小明, 汤宏亮, 杨树峰. Fe_xO-SiO₂-CaO-MgO-“NiO”系镍渣势函数及分子动力学模拟[J]. 计算物理, 2021, 38(2): 215-223.
[8]	王雪梅, 董斌, 朱子亮, 杨俊升. 聚合物分子与官能化纳米管相互作用及扩散特性的分子动力学模拟[J]. 计算物理, 2020, 37(5): 589-594.
[9]	和二斌, 罗志荣, 朱留华. 肌红蛋白力致去折叠的全原子分析[J]. 计算物理, 2020, 37(2): 205-211.
[10]	周璐, 马红和. 超临界水中硫酸钠结晶动力学的分子动力学模拟[J]. 计算物理, 2020, 37(2): 212-220.
[11]	史晓蕊, 刘振宇, 吴慧英. 纳米孔壁面作用对蛋白质过孔影响的粗粒化分子动力学模拟[J]. 计算物理, 2020, 37(1): 63-68.
[12]	柴汝宽, 刘月田, 王俊强, 辛晶, 皮建, 李长勇. 分子动力学模拟方解石和白云石润湿性[J]. 计算物理, 2019, 36(4): 474-482.
[13]	王帅创, 张弓木, 孙博, 宋海峰, 田明锋, 方俊, 刘海风. 量子分子动力学模拟液体钚的输运性质[J]. 计算物理, 2019, 36(3): 253-258.
[14]	梁华, 李茂生. 孔洞和空位对单晶铝力学性能影响的分子动力学研究[J]. 计算物理, 2019, 36(2): 211-218.
[15]	张海燕, 殷新春. 简单金属固液界面固化过程生长机制的分子动力学研究[J]. 计算物理, 2019, 36(1): 80-88.

金红石TiO₂辐照损伤模拟研究

A Simulation Study on Irradiation Damage of Rutile TiO₂

RichHTML

PDF

可视化

摘要/Abstract

引用本文

使用本文

图/表 8

参考文献 35

相关文章 15

编辑推荐

Metrics

作者中心

审稿中心

期刊浏览

期刊介绍